A beam of width t incident at on an air-water boundary. The width of the beam in water is ________
To find the width of the beam in water when it is incident at an angle of 45 degrees on an air-water boundary, we can follow these steps:
Step 1: Understand the Geometry
When the beam of width T strikes the air-water boundary at an angle of 45∘, we can visualize the situation using a diagram. The beam will refract as it enters the water, and we need to determine how its width changes.
Step 2: Use Trigonometry
In the triangle formed by the incident beam in air and the refracted beam in water, we can relate the widths using the cosine of the angles. The width in air is T, and the width in water will be denoted as T′.
Using the relationship from the geometry:
AB=Tcos(45∘)
AB=T′cos(r)
where r is the angle of refraction in water.
Step 3: Relate the Widths
From the above equations, we can set them equal to each other:
Tcos(45∘)=T′cos(r)
This implies:
T′=T⋅cos(r)cos(45∘)
Step 4: Apply Snell's Law
According to Snell's Law:
μ=sin(45∘)sin(r)
Given that sin(45∘)=1√2, we can express this as:
sin(r)=1μ√2
Step 5: Convert Sine to Cosine
Using the identity sin2(r)+cos2(r)=1, we can find cos(r):
cos2(r)=1−sin2(r)=1−(1μ√2)2
cos2(r)=1−12μ2
cos(r)=√1−12μ2
Step 6: Substitute Back to Find T′
Now substitute cos(r) back into the equation for T′:
T′=T⋅√1−12μ2cos(45∘)
Since cos(45∘)=1√2:
T′=T⋅√2⋅√1−12μ2
Final Expression
Thus, the width of the beam in water is:
T′=T⋅√2⋅√1−12μ2
When the beam of width T strikes the air-water boundary at an angle of 45∘, we can visualize the situation using a diagram. The beam will refract as it enters the water, and we need to determine how its width changes.
In the triangle formed by the incident beam in air and the refracted beam in water, we can relate the widths using the cosine of the angles. The width in air is T, and the width in water will be denoted as T′.
AB=Tcos(45∘)
AB=T′cos(r)
where r is the angle of refraction in water.
From the above equations, we can set them equal to each other:
Tcos(45∘)=T′cos(r)
This implies:
T′=T⋅cos(r)cos(45∘)
According to Snell's Law:
μ=sin(45∘)sin(r)
Given that sin(45∘)=1√2, we can express this as:
sin(r)=1μ√2
Using the identity sin2(r)+cos2(r)=1, we can find cos(r):
cos2(r)=1−sin2(r)=1−(1μ√2)2
cos2(r)=1−12μ2
cos(r)=√1−12μ2
Now substitute cos(r) back into the equation for T′:
T′=T⋅√1−12μ2cos(45∘)
Since cos(45∘)=1√2:
T′=T⋅√2⋅√1−12μ2
Thus, the width of the beam in water is:
T′=T⋅√2⋅√1−12μ2
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Exercise1.4
Explore 12 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Exercise1.5
Explore 22 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Exercise1.2
Explore 20 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSExercise:dpp 3.3
Explore 15 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
Similar Questions
A beam of white light is incident on a hollow prism of glass. Then

View SolutionA coverging beam of light is incident on the concave mirror. Then the reflected light :
View SolutionA ray of light is incident upon an air/water interface ( it passes from air into water) at an angle of 45∘ . Which of the following quantities change as the light enters the water?
(I) wavelength (II) frequency (III) speed of propagation (IV) direction of propagation
View SolutionA narrow parallel beam of light is incident on a transparent sphere of refractive index n if the beam finally gets focused at a point situated at a distance=2×(radius of sphere) form the center of the sphere then find n?
View SolutionThere is layer of medium of variable refractive index μ=√2−1√2y (where 0≤t<1/2) sandwitched between the layer of glass and air A beam of light travelling in air at an angle 45∘ has a width Δω. When the beam enters the layer of glass its width becomes : (μglass=√2)
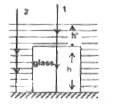
View SolutionTwo beams of light are incident normally on water (R.l. = 43). If the beam 1 passes through a glass (R.l. = 32) slab of height h as shown in the figure, the time difference for both beams for reaching the bottom is
View SolutionA beam of white light is incident normaly on a plane surface absorbing 70% of the light and reflecting the rest. If the incident beam carries 10 w of power, find the force exerated by it on the surface.
View SolutionA parallel beam of monochromatic light of wavelength 500 nm is incident normally on a rectangular slit. The angular width of the central fringe of Fraunhofer diffraction is found to be 60∘. Find the width of the slit in metre.
View SolutionA parallel beam of light is incident normally on a plane surface absorbing 40% of the light and reflecting the rest. If the incident beam carries 60 W of power, the force exerted by it on the surface is
View SolutionSTATEMENT -1: A white parallel beam of light is incident on a plane glass-vacuum interface as shown. The beam may not undergo dispesion after suffering deviation at the interface (The beam is not incident normally on the interface.)

STATEMENT -2: Vacuum has same refractive index for all colours of white light.
View Solution