Due to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as n=n0√1+ay, where n0 is the index of refraction at the surface and a=2.0×10−6m−1 . A person of height h=2.0m stands on a level surface. Beyond what distance will he not see the runway?

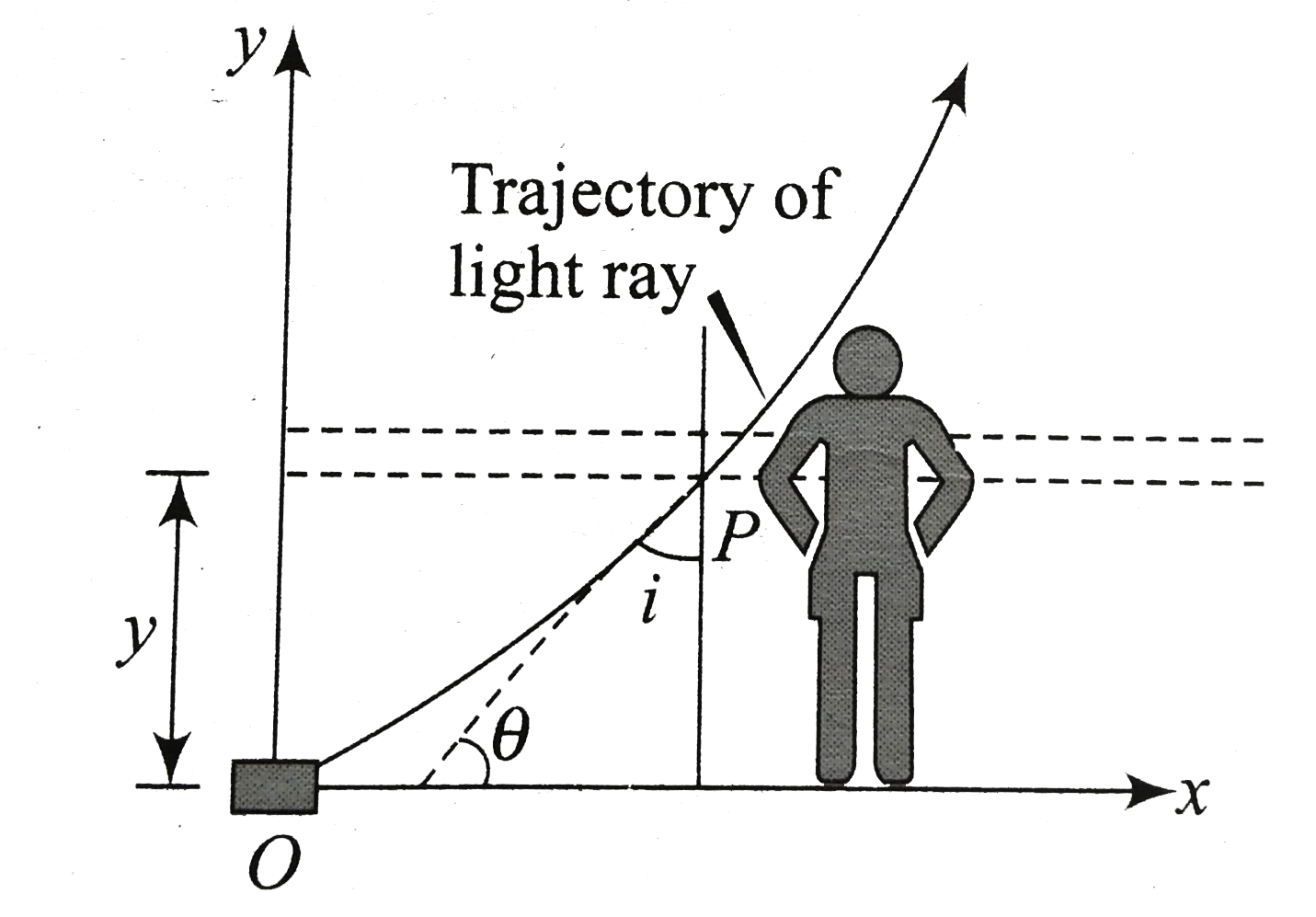
As refractive index is changing along y-direction, we can assum a number of thing layers of air placed parallel to x-axis. Let O be the distant object just visible to the man. Consider a layer of air at a distance y from the ground. Let P be a point on the trajectory of the ray. Form Fig. , θ=90∘−i .
The slope of trangent at point P is tanθ=dy/dx=coti .
From Snell's law, n sin i= constant
At the surface, n=n0 and i=90∘ .
n0sin90∘=nsini=(n0√1+ay)sini
sini=1√1+ay⇒coti=dydx=√ay
∫y0dy√ay=∫x0dx⇒x=2√ya
On substituting y=2.0m and a=2×10−1 , we have
xmax=2√22×10−6=2000m
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Solved Examples
Explore 15 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Exercise1.1
Explore 14 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSExercise:dpp 3.3
Explore 15 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
Similar Questions
A man of height 2 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road and a=2×10−6/m. What is the actual length of the road, man is able to see
View SolutionA man of height 1.47 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road a =1.5×10−6/m. What is the apparent length of the road man is able to sec?
View Solution
Knowledge Check
The focal length of a biconvex lens of refractive index 1.5 is 0.06m. Radii of curvature are in the ratio 1:2. Then radii of curvature of two lens surfaces are
A0.045m,0.09mB0.09m,0.18mC0.04m,0.08mD0.06m,0.12m
A man of height 2.0m is standing on a level road because of temprature variation the refractive index of air is varying as μ=√1+ay, where y is height from road. If a=2.0×10−6m−1. Then, find distant point that he can see on the road.
View SolutionA biconvex thin lens is prepared from glass of refractive index μ2=32. The two conducting surfaces have equal radii of 20 cm each. One of the the surface is silvered from outside to make it reflecting. It is placed in a medium of refractive index μ1=53. It acts as a
View SolutionA light ray enters into a medium whose refractive index varies along the x-axis as n(x)=n0√1+x4 where n0=1. The medium is bounded by the plates x=0,x=1 & y=0. It the ray enters at the origin at an angle 30∘ with x-axis

View SolutionDefine refractive index of a tranparent medium . The speed of light in a medium of absolute refractive index 1.5 is 2×108ms−1 . What is the speed of light in vacuum ?
View SolutionA point source of light is placed at a distance h below the surface of a large deep lake.
(a) Show that the fraction f of the light energy that escapes directly from the water surface is independent of h and is given by f=12−12n√n2−1 where n is the index of refraction of water.
(Note: Absorption within the water and reflection at the surface, except where it is total, have been neglected)
(b) Evaluate this ratio for n=4/3.
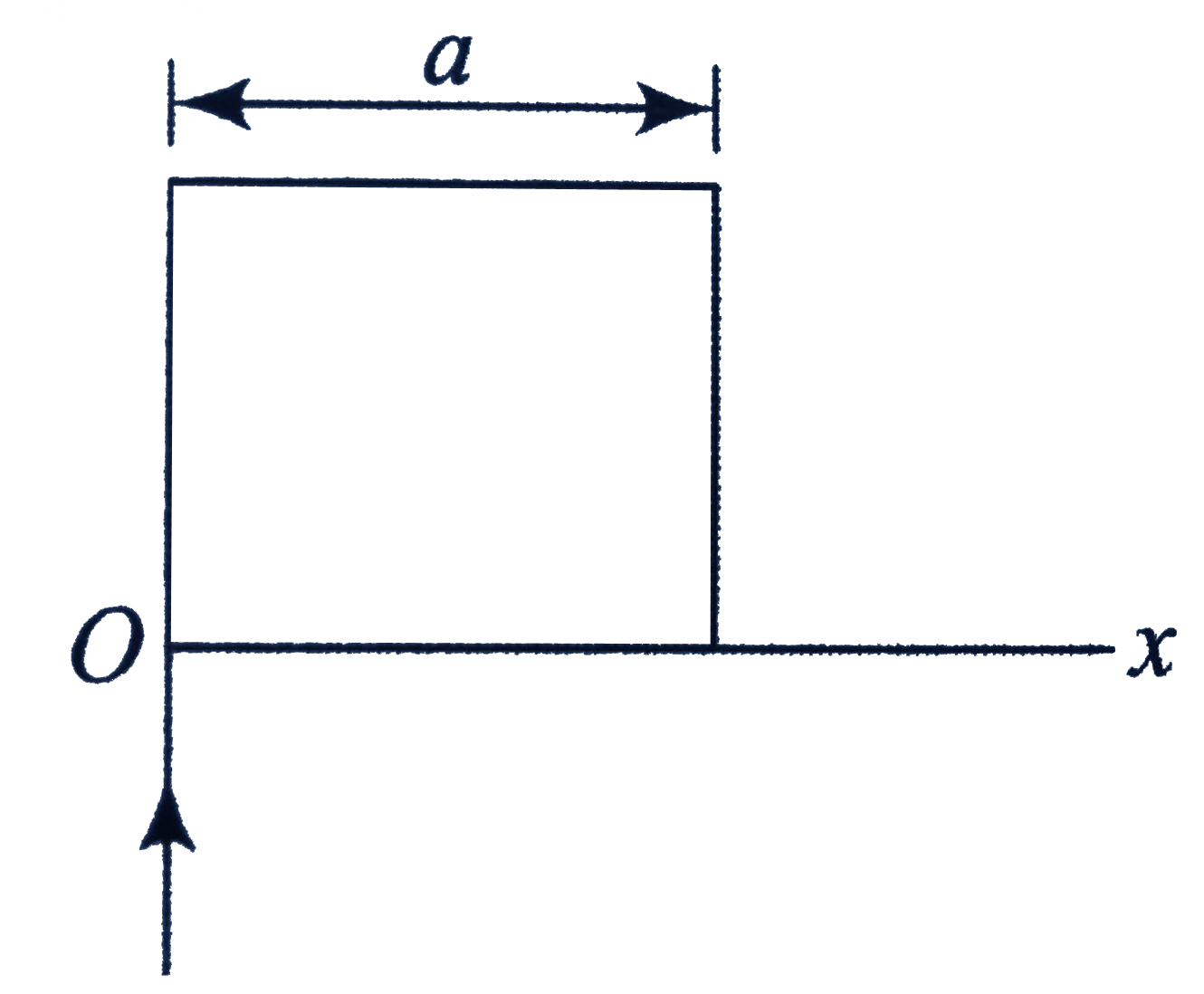
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View SolutionThe figure shows a transparent slab of length m placed in air whose refractive index in x direction varies as μ=1+x2(0<x<1). The optical path length of ray R will be

View Solution

