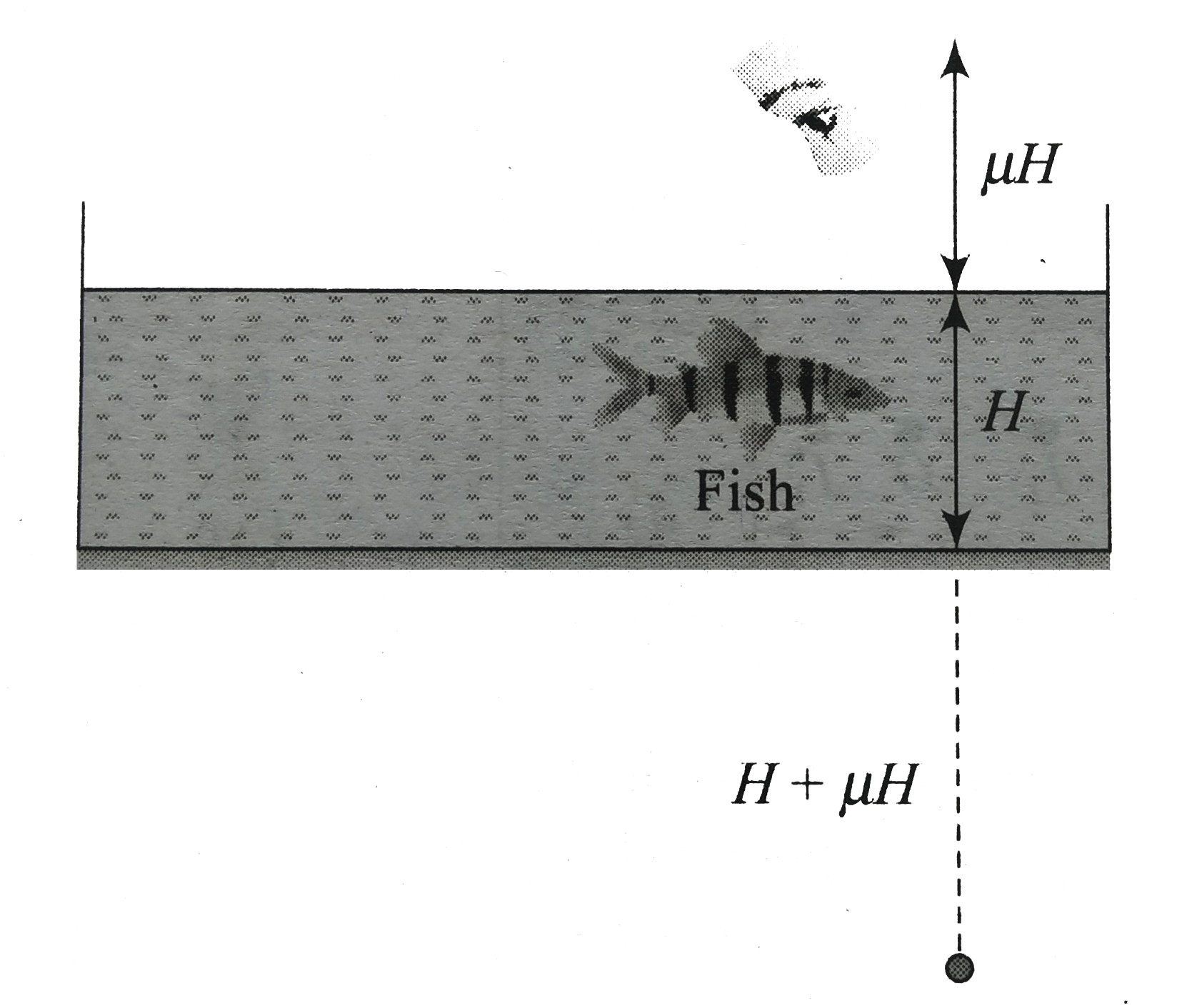
Consider the situation in Fig. The bottom of the pot is a reflecting plane mirror, S is a small fish, and T is a human eye. Refractive index of water is μ.
a. At what distance(s) from itself will the fish see the image(s) of the eye?
b. At what distance(s) from itself will the eye see the image(s) of the fish?

a. The fish will observe the images of eye one from direct observation and the other reflected image from the plane mirror.
(i) Direct observation of eye from fish
Apparent height, H′=Hnrel=Hnairnwater=H(1μ)
Hence, H′=μH
Distance of image of eye from fish
d=H2+μH=H(12+μ)
(ii) Observation of reflected image of the eye from the fish
For mirror, the distance of eye from it will be (H+μH). Hence, the image of eye from mirror will be (H+μH) behind the mirror. Hence, distance of image of eye from the fish
d′=H2+H+μH=32H+μH
⇒d′=H(32+μ)
b. The eye will also observe two images of the fish, one from direct observation and the other reflected image from the mirror.
(i) Direct observation of fish from eye:
Apparent depth of the fish observed by the eye
H′=H/2nr=H/2nwaternair=H/2μ=H2μ Distance of image of the fish from the eye,
d=H+H2μ=H(1+12μ)
(ii) Eye observing image of fish:
The eye will observe the image of fish reflected from the mirro.
Apparent depth of image of the fish from air and water interface.
H′= Real depth n rel =32H(nwaternair)
Here real depth from top surface of water
=H+H2=32H
H′=3H2μ
Hence, distance between t his image and the eye,
d′=H+3H2μ=H+3(1+32μ)
 ,
,

Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Solved Examples
Explore 15 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Exercise1.1
Explore 14 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSExercise:dpp 3.3
Explore 15 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
Similar Questions
An air bubble inside water. The refractive index of water is 4/3 . At what distance from the air bubble should a point object be placed so as to form a real image at the same distance from the bubble:-
View SolutionAn insect is sitting in front of a plane mirror at a distance 1 m from it.
a. Where is the image of the insect formed?
b.What is the distance between the insect and its image?
View SolutionSee Fig. and answer the following question.
a. Find apparent height of the bird.
b. Find apparent depth of the fish.
c. At what distance will the bird appear to the fish ?
d. At what distance will the fish appear to the bird?

View SolutionAn object is placed at 24 cm distant from a surface of a lake. If water has refractive index of 4/3, then at what distance from the lake surface, a fish will get sight of an object.
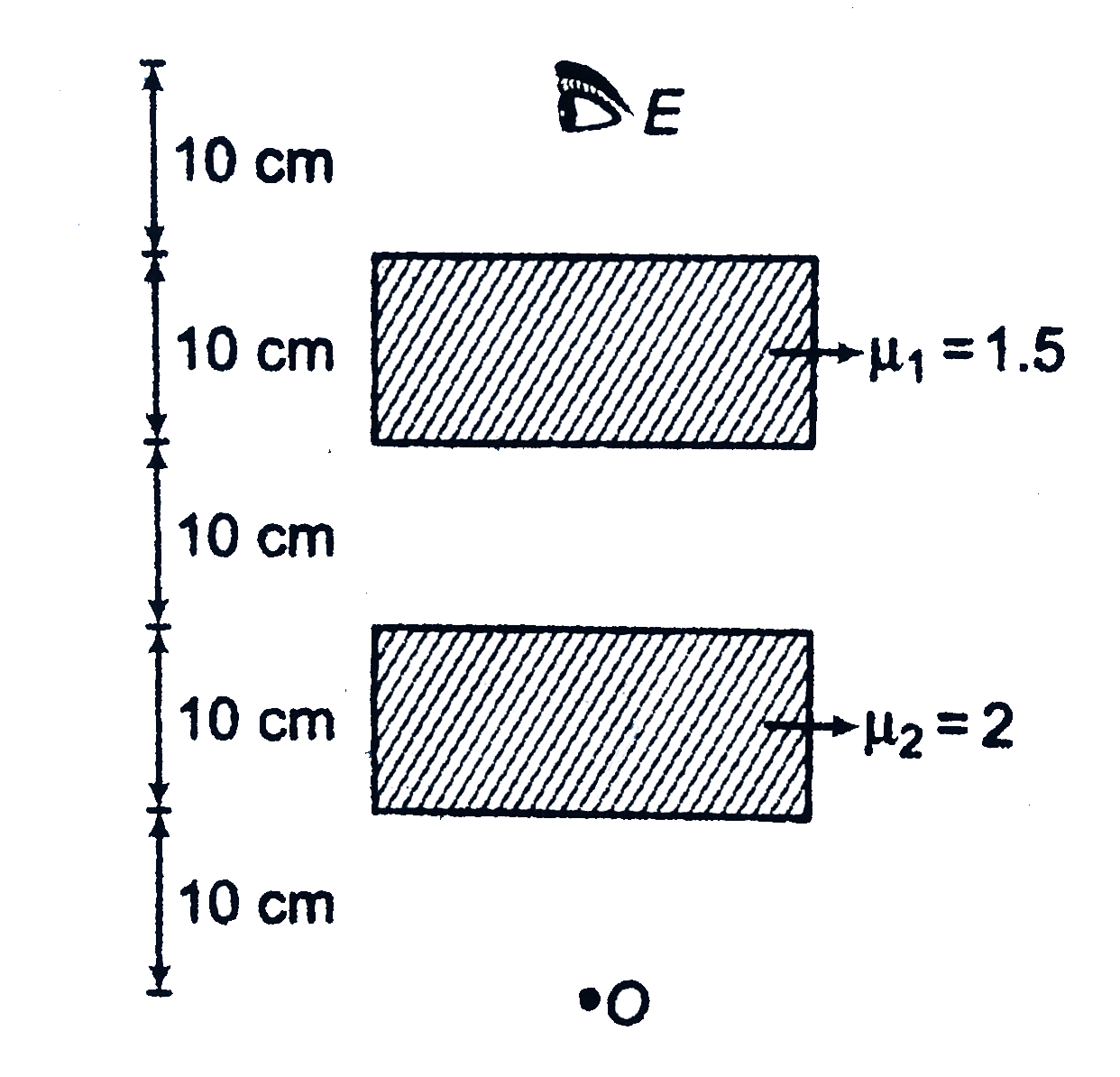
View SolutionAt what distance eye E will observe the fourth image (after four refractions from plane surfaces) of object O from itself.
View SolutionWhat happens to the image distance in the eye when we increase the distance of an object from the eye ?
View SolutionIn figure, a point source S is placed at a height h above the plane mirror in a medium of refractive index μ.
a. Find the number of images seen for normal view.
b. Find the distance between the images.

View SolutionIn a thin spherical fish bowl of radius 10 cm filled with water of refractive index 4/3 there is a small fish at a distance of 4 cm from the centre C as shown in the figure. Where will the image of fish appears, if seen from E.

View SolutionConsider the situation shown in figure. A plane mirror is fixed at a height h above the bottom of a beaker containing water (refractive index μ) up of a bottom formed by the mirror.Find the position of the image of bottom formed by the mirror.

View SolutionA hemishperical surface of radius R and refractive index μ=1.5 is polished as shown. At what distance x from point P a point object O be placed so that its image coincides with the object itself?

View Solution