Three identical resistors are connected in series . When a certain potential difference is applied across the combination , the total power would be dissipated is 27W. How many times the power would be dissipated if the three resistors were connected in parallel across the same potential difference ?
The correct Answer is:9
To solve the problem step by step, we will analyze the power dissipation in both series and parallel configurations of the resistors.
Step 1: Understand the Series Configuration
When three identical resistors (each of resistance R) are connected in series, the total resistance Req, series is given by:
Req, series=R+R+R=3R
Step 2: Calculate Power in Series
The power P dissipated in a resistor is given by the formula:
P=V2Req
For the series configuration, substituting Req, series:
Pseries=V23R
According to the problem, the total power dissipated in the series configuration is 27W:
V23R=27
From this, we can express V2 in terms of R:
V2=27×3R=81R
Step 3: Understand the Parallel Configuration
Now, when the same three resistors are connected in parallel, the equivalent resistance Req, parallel is given by:
1Req, parallel=1R+1R+1R=3R
Thus, the equivalent resistance for the parallel configuration is:
Req, parallel=R3
Step 4: Calculate Power in Parallel
Using the power formula again for the parallel configuration:
Pparallel=V2Req, parallel
Substituting Req, parallel:
Pparallel=V2R3=3V2R
Step 5: Substitute V2 from Series into Parallel Power
Now, we substitute V2 from our earlier calculation:
Pparallel=3×81RR=243W
Step 6: Calculate the Ratio of Power Dissipation
To find how many times the power dissipated in parallel is compared to series:
Ratio=PparallelPseries=24327=9
Final Answer
The power dissipated when the three resistors are connected in parallel is 9 times the power dissipated when they are connected in series.
---
When three identical resistors (each of resistance R) are connected in series, the total resistance Req, series is given by:
Req, series=R+R+R=3R
The power P dissipated in a resistor is given by the formula:
P=V2Req
For the series configuration, substituting Req, series:
Pseries=V23R
According to the problem, the total power dissipated in the series configuration is 27W:
V23R=27
From this, we can express V2 in terms of R:
V2=27×3R=81R
Now, when the same three resistors are connected in parallel, the equivalent resistance Req, parallel is given by:
1Req, parallel=1R+1R+1R=3R
Thus, the equivalent resistance for the parallel configuration is:
Req, parallel=R3
Using the power formula again for the parallel configuration:
Pparallel=V2Req, parallel
Substituting Req, parallel:
Pparallel=V2R3=3V2R
Now, we substitute V2 from our earlier calculation:
Pparallel=3×81RR=243W
To find how many times the power dissipated in parallel is compared to series:
Ratio=PparallelPseries=24327=9
The power dissipated when the three resistors are connected in parallel is 9 times the power dissipated when they are connected in series.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Calculating Thermal Power in Resistance
Explore 14 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 27 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICS ENGLISHChapter:HEATING EFFECT OF CURRENTExercise:Comprehension
Explore 13 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:GEOMETRICAL OPTICSExercise:Integer Type
Explore 4 Videos
- INDUCTANCEBook:CENGAGE PHYSICS ENGLISHChapter:INDUCTANCEExercise:Concept Based
Explore 8 Videos
Similar Questions
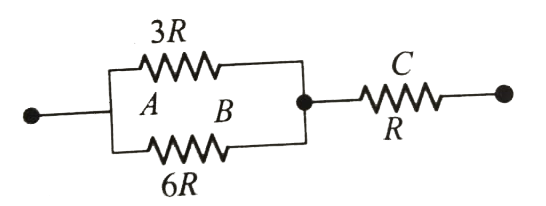
Figure 7.37 shows a network of three resistances. When some potential difference is applied across the network , thermal powers dissipated by A,BandC are in the ratio
View SolutionThree equal resistors connected in series across a source of emf together dissipate 10W of power. What would be the power dissipated if te same resistors are connected in parallel across the same source of emf?
View SolutionThree equal resistors connected in series across a source of e.m.f. together dissipate 10 W of power. What should be the power dissipated if the same resistors are connected in parallel across the same source of e.m.f.
View SolutionA resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the current in the circuit,
View SolutionThree resistors are connected to a 6 V battery as shown in the figure
Calculate:
potential difference across the 7.2 ohm resistor
View SolutionThree equal resistor connected in series across a source of enf together dissipate 10Wa. If the same resistors aer connected in parallel across the same emf, then the power dissipated will be
View Solution3 identical bulbs are connected in series and these together dissipate a power P . If now the bulbs are connected in parallel, then the power dissipated will be
View SolutionTwo capacitances of capacity C1and C2 are connected in series and potential difference V is applied across it. Then the potential difference across C1 will be
View SolutionWhen three identical bulbs are connected in series. The consumed power is 10W. If they are now connected in pa rallel then the consumed power will be:-
View SolutionA resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the potential difference across the 6 Ω resistor.
View Solution