A heater is designed to operate with a power of 1000 W in a 100 V line. It is connected in combination with a resistance of 10Ω and a resistance R, to a 100 V mains as shown in the figure. What will be the value of R so that the heater operates with a power of 62.5 W?
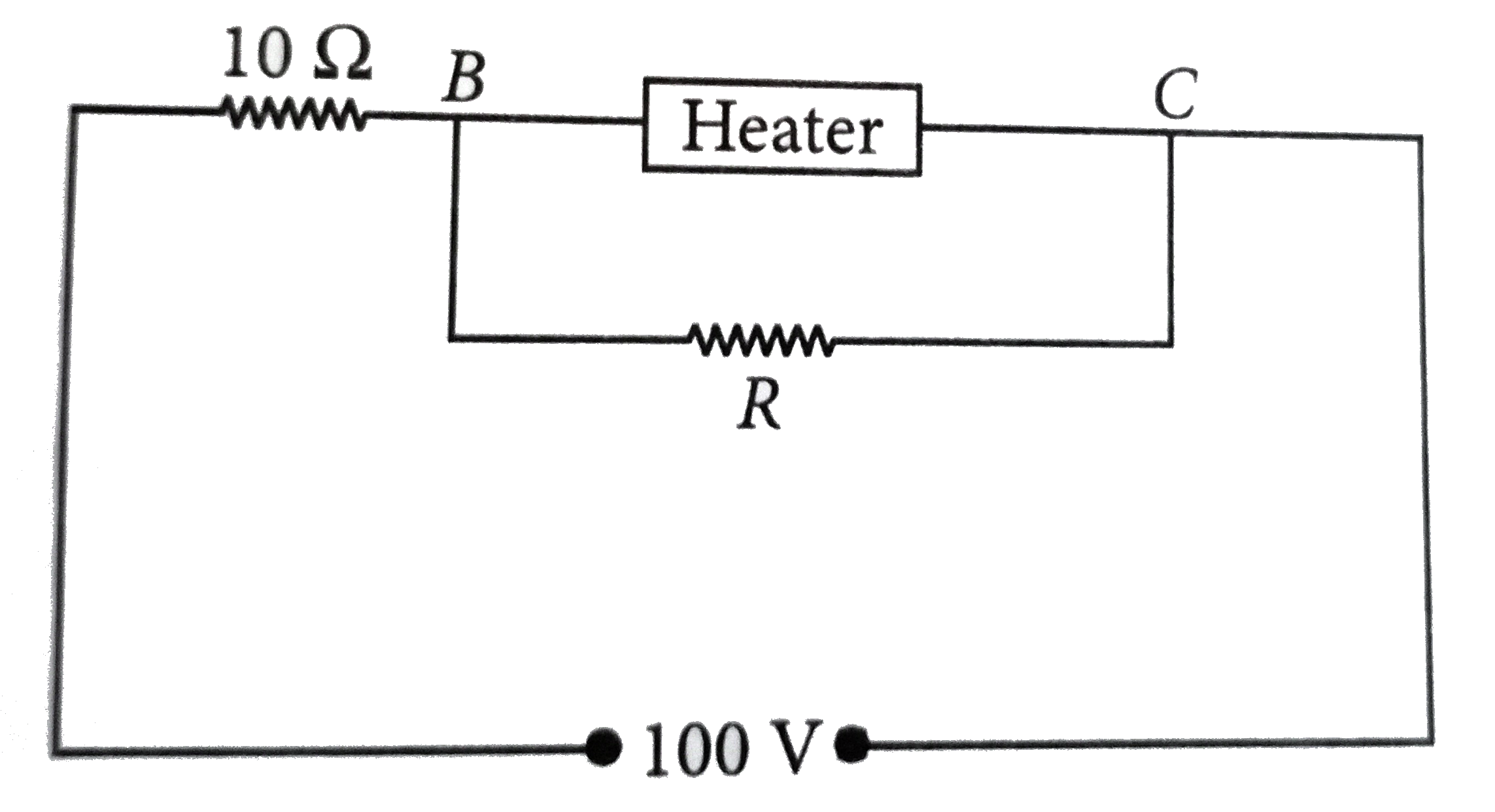
The resistance of the heater is
R=V2P
=100×1001000=10Ω
The power on which it operates is 62.5W. Therefore,
V=√R×P'=√10×62.5=√625=25V
So the potential drop across AB is 75V.
Therefore, the current in AB is
I=VR=7510=7.5A
This currents gets divided into two parts . Let I1 be the current that passes through the heater . Therefore,
25=I1×10orI1=2.5A
Hence, the current through R is 5A.
Applying ohm's law across R , we get
25=5×RorR=5Ω
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Exercise 7.1
22 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective
8 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
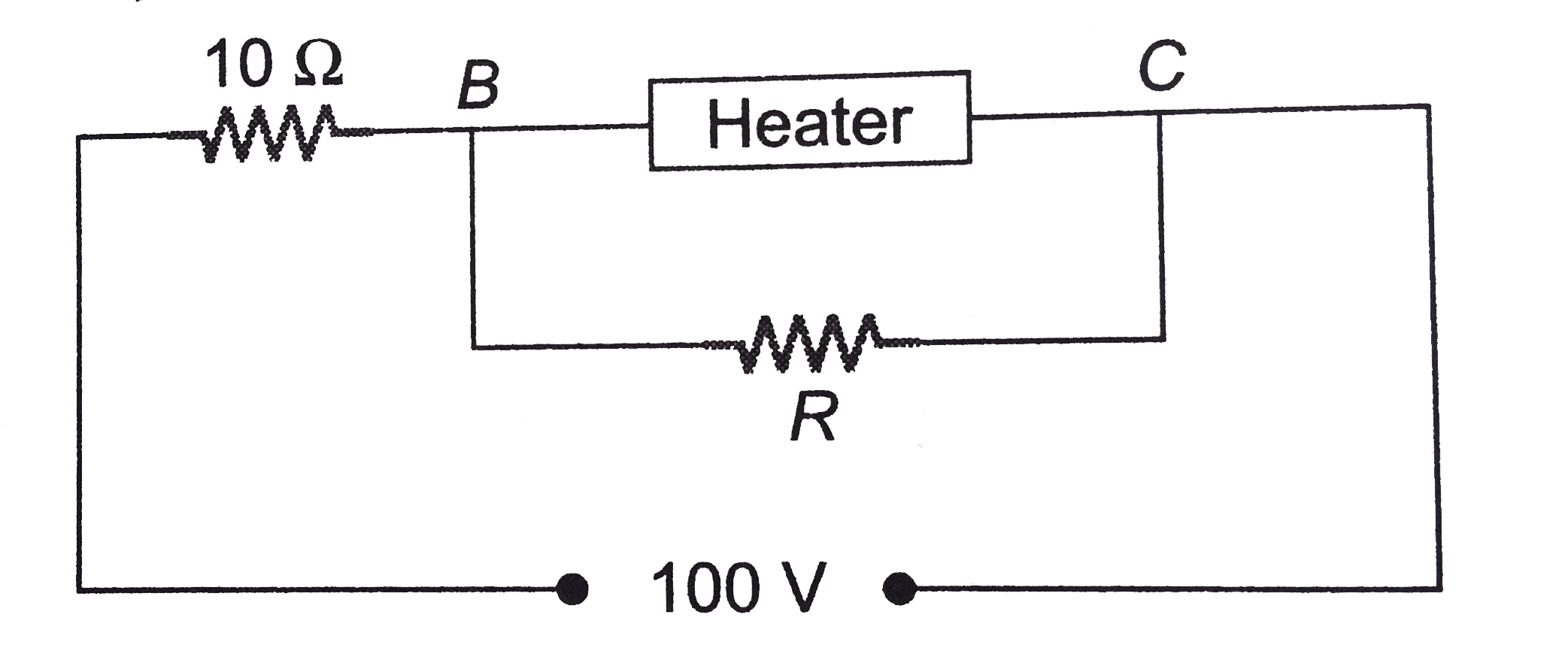
A heater is designed to operate with a power of 1000W in a 100V line. It is connected in combination with a resistance of 10Ω and a resistance R, to a 100V mains as shown in figure. What will be the value of R so that the heater operates with a power of 62.5W?
View SolutionThe power dissipated in the circuit shown in the figure is 30 W. The value of R is
View Solution
Knowledge Check
A heater is designed to operate with a power of 1000W in a 100V line. It is connected in combination with a resistance of 10Ω and a resistance R, to a 100V mains as shown in figure. What will be the value of R so that the heater operates with a power of 62.5W?
 A15ΩB10ΩC5ΩD25Ω
A15ΩB10ΩC5ΩD25Ω
Five identical lamps each of resistance R = 1500 Ω are connected to 300 V as shown in figure . The reading of ideal ammeter A is
View SolutionA 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

View SolutionA 10 V battery of negilgible internal resistance is connected across a 200V battery and a resistance of 38Ω as shown in figure.
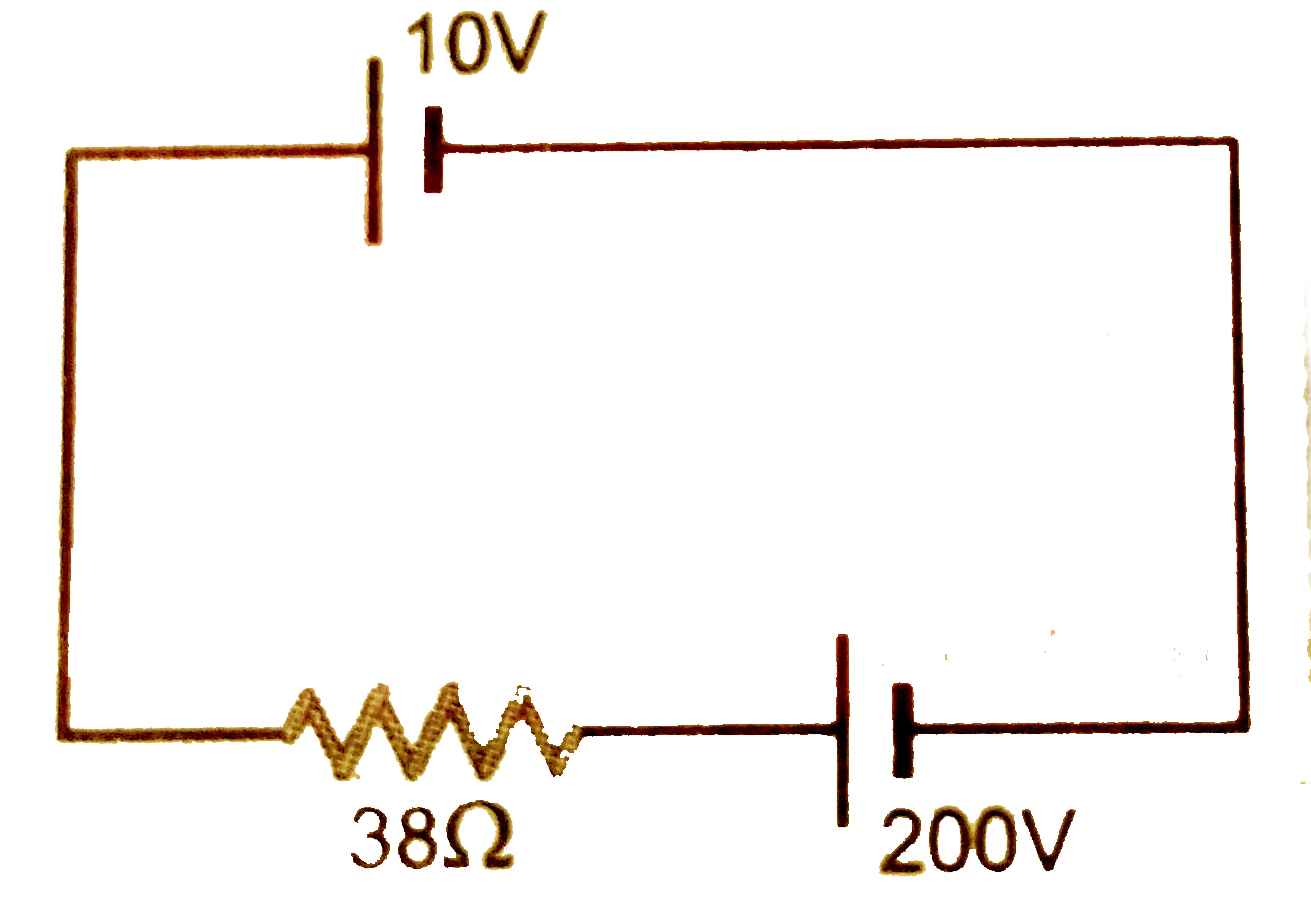 . Find the value of current in the circuit.
. Find the value of current in the circuit.
View SolutionA 100V voltmeter of internal resistance 20kΩ in series with a high resistance R is connected to a 110V line. The voltmeter reads 5V, the value of R is
View SolutionA 5V battery with internal resistance 2Ω and a 2V battery with internal resistance1Ω are connected to a 10Ω resistor as shown in the figure.
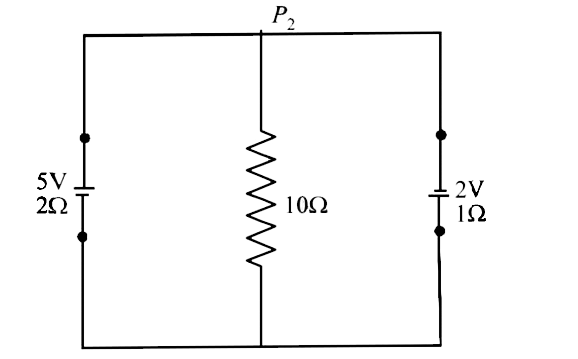
The current in the 10Ω resistor is
View SolutionThe resistance of a heater coil is 110Ω. A resistance R is connected in parallel with it and the combination is joined in series with a resistance of 11Ω to a 220V main line. The heater operates with a power of 110W. The value of R in Ω is
View SolutionA 100W bulb designed to operate on 100V is to be connected across a 500V source . Find the resistance to be put in series so that bulb consumes 100W only.
View Solution

