What amount of heat will be generated in a coil of resistance R due to a charge q passing through it if the current in the coil
a. decreases down to zero uniformly during a time interval t0?
b. decrases down to zero having its value every t0 seconds?
To solve the problem, we will break it down into two parts as per the question.
Part (a): Heat generated when current decreases uniformly to zero over time interval t0
1. Define the initial current: Let the initial current at t=0 be I0. At t=t0, the current becomes 0.
2. Express current as a function of time: Since the current decreases uniformly, we can express the current I(t) as:
I(t)=I0(1−tt0)
3. Calculate the charge q: The charge q that passes through the coil can be calculated by integrating the current over the time interval from 0 to t0:
q=∫t00I(t)dt=∫t00I0(1−tt0)dt
Evaluating this integral:
q=I0(t−t22t0)t00=I0(t0−t202t0)=I0(t0−t02)=I0t02
4. Relate current to charge: From the expression for charge, we can express I0:
I0=2qt0
5. Calculate heat generated H: The heat generated in the coil can be calculated using Joule's law:
H=∫t00I2Rdt=∫t00(I0(1−tt0))2Rdt
This simplifies to:
H=RI20∫t00(1−tt0)2dt
Evaluating the integral:
∫t00(1−tt0)2dt=(t−t22t0+t33t20)t00=t0−t202t0+t303t20=t0−t02+t03=t06
Therefore, substituting back:
H=RI20⋅t06
Replacing I0:
H=R(2qt0)2⋅t06=4q2R6t0=2q2R3t0
Part (b): Heat generated when current decreases to zero at intervals of t0
1. Define the current: The current decreases in discrete steps. We can express the current at each interval as:
I(t)=I0(12)tt0
2. Calculate the charge q: The charge can be calculated by integrating the current over the time interval:
q=∫t00I(t)dt=∫t00I0(12)tt0dt
This evaluates to:
q=I0t0⎛⎝−1ln(2)(12)tt0⎞⎠t00=I0t0(−1ln(2)(12)−(−1ln(2)))=I0t0ln(2)
3. Relate current to charge: From the expression for charge, we can express I0:
I0=qln(2)t0
4. Calculate heat generated H: The heat generated in the coil can be calculated using Joule's law:
H=∫t00I2Rdt=∫t00⎛⎝I0(12)tt0⎞⎠2Rdt
This simplifies to:
H=RI20∫t00(12)2tt0dt
Evaluating the integral:
∫t00(12)2tt0dt=−t02ln(2)(12)2tt0∣∣∣t00=−t02ln(2)(14−1)=t02ln(2)⋅34=3t08ln(2)
Therefore, substituting back:
H=RI20⋅3t08ln(2)
Replacing I0:
H=R(qln(2)t0)2⋅3t08ln(2)=3q2Rln(2)8t0
Final Answers:
- Part (a): The heat generated is H=2q2R3t0
- Part (b): The heat generated is H=3q2Rln(2)8t0
2. Express current as a function of time: Since the current decreases uniformly, we can express the current I(t) as:
I(t)=I0(1−tt0)
q=∫t00I(t)dt=∫t00I0(1−tt0)dt
Evaluating this integral:
q=I0(t−t22t0)t00=I0(t0−t202t0)=I0(t0−t02)=I0t02
I0=2qt0
H=∫t00I2Rdt=∫t00(I0(1−tt0))2Rdt
This simplifies to:
H=RI20∫t00(1−tt0)2dt
Evaluating the integral:
∫t00(1−tt0)2dt=(t−t22t0+t33t20)t00=t0−t202t0+t303t20=t0−t02+t03=t06
Therefore, substituting back:
H=RI20⋅t06
Replacing I0:
H=R(2qt0)2⋅t06=4q2R6t0=2q2R3t0
I(t)=I0(12)tt0
q=∫t00I(t)dt=∫t00I0(12)tt0dt
This evaluates to:
q=I0t0⎛⎝−1ln(2)(12)tt0⎞⎠t00=I0t0(−1ln(2)(12)−(−1ln(2)))=I0t0ln(2)
I0=qln(2)t0
H=∫t00I2Rdt=∫t00⎛⎝I0(12)tt0⎞⎠2Rdt
This simplifies to:
H=RI20∫t00(12)2tt0dt
Evaluating the integral:
∫t00(12)2tt0dt=−t02ln(2)(12)2tt0∣∣∣t00=−t02ln(2)(14−1)=t02ln(2)⋅34=3t08ln(2)
Therefore, substituting back:
H=RI20⋅3t08ln(2)
Replacing I0:
H=R(qln(2)t0)2⋅3t08ln(2)=3q2Rln(2)8t0
- Part (a): The heat generated is H=2q2R3t0
- Part (b): The heat generated is H=3q2Rln(2)8t0
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Exercise 7.1
22 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective
8 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
What will be genotypic ratio in the F2 generation of a monohybrid cross ?
View SolutionWhat amount of heat will be generated in a coil resistance R due to a charge q passing through it if the current in the coil decreases down to zero uniformly during a time interval Δt ?
View SolutionWhat amount of heat will be generated in a coil of resistance R due to a charge q passing through it if the current in the coil
a. decreases down to zero uniformly during a time interval t0?
b. exponentially decrases down to zero having its value every t0 seconds?
View SolutionA cell of emf ε and internal resistance r is charged by a current I, then
View SolutionA magnetic flux through a stationary loop with a resistance R varies during the time interval τ as ϕ=at(τ−t). Find the amount of heat the generated in the loop during that time
View SolutionTwo coil A and B have coefficient of mutual inductance M=2H. The magnetic flux passing through coil A charges by 4 Weber in 10 seconds due to the change in current in B. Then
View SolutionA capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
View SolutionA thermocol vessel contains 0.5kg of distilled water at 30∘C. A metal coil of area 5×10−3m2, number of turns 100, mass 0.06kg and resistance 1.6Ω is lying horizontally at the bottom of the vessel. A uniform time-varying magnetic field is set up to pass vertically through the coil at time t=0. The field is first increased from zero to 0.8T at a constant rate between 0 and 0.2s and then decreased to zero at the same rate between 0.2and0.4s. the cycle is repeated 12000 times. Make sketches of the current through the coil and the power dissipated in the coil as function of time for the first two cycles. Clearly indicate the magnitude of the quantities on the axes. Assumes that no heat is lost to the vessel or the surroundings. Determine the final tempreture of water under thermal equilibrium. Specific heat of metal =500jkg−1K−1 and the specific heat of water =4200jkg−1K−1. Neglect the inductance of coil.
View SolutionTwo concentric and coplanar coils have radii a and b(>>a) as shows in Fig. Resistance of the inner coil is R. Current in the outer coil is increased from 0 to i, then the total charge circulating the inner coil is

View SolutionA source of emf E=10V and having negligible internal resistance is connected to a variable resistance.The resistance varies as shown in figure. The total charge that has passed through the resistor R during the time interval from t1 or t2 is
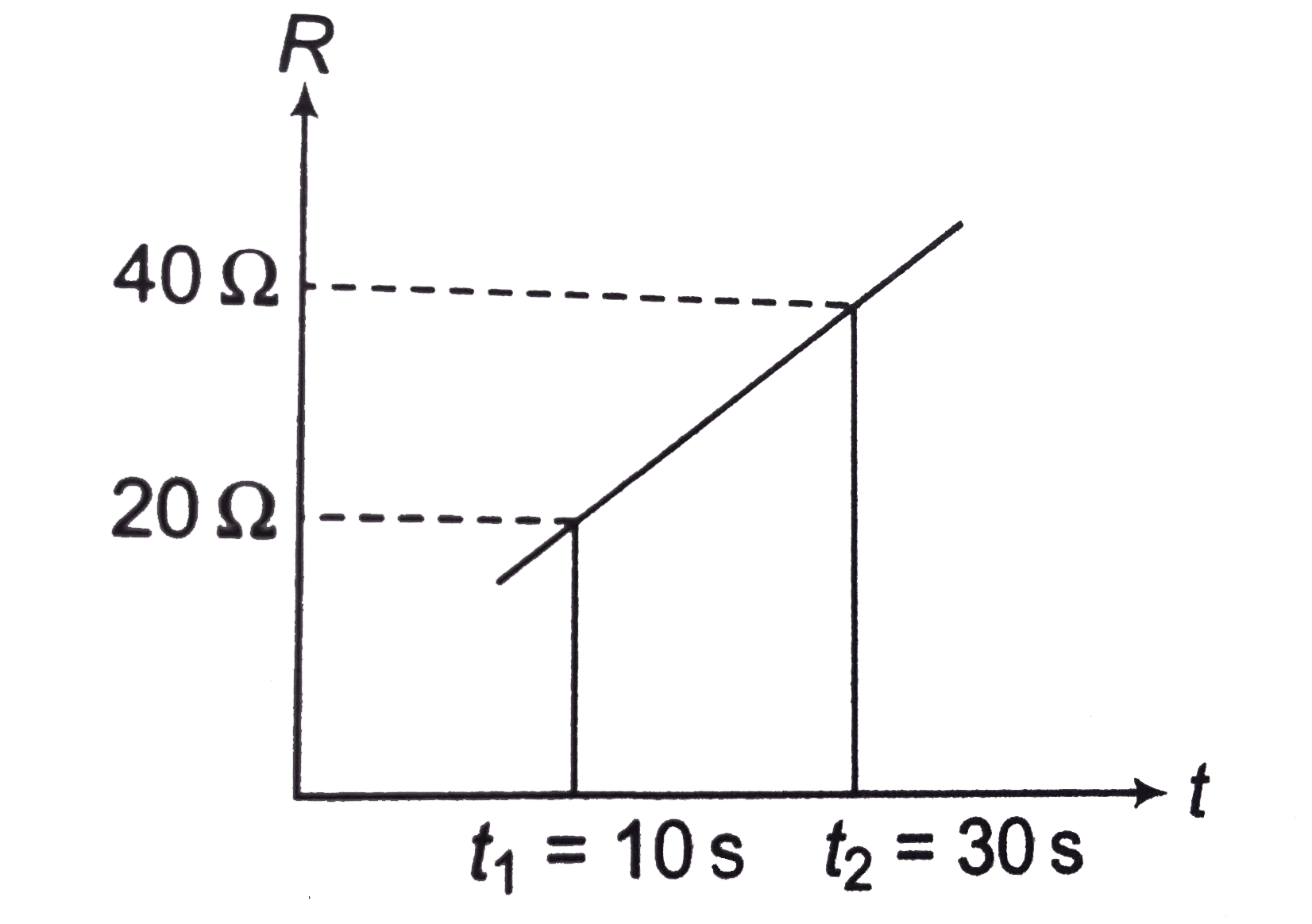
View Solution
