How will you connect ( series and parallel ) 24cells each of internal resistance 1Ω to get maximum power output across a load of 10Ω?
To solve the problem of how to connect 24 cells, each with an internal resistance of 1 ohm, to achieve maximum power output across a load of 10 ohms, we can follow these steps:
1. Understand the Condition for Maximum Power:
- The maximum power transfer theorem states that maximum power is transferred when the total internal resistance of the source (cells) equals the external load resistance.
- Therefore, we need to set the equivalent internal resistance of the cells equal to the load resistance (10 ohms).
2. Define the Configuration:
- Let’s denote:
- m = number of rows (parallel connections)
- n = number of cells in each row (series connections)
- The total number of cells is given by:
m×n=24
3. Calculate the Total Internal Resistance:
- If n cells are connected in series, the total internal resistance for one row is:
Rinternal, one row=n×1Ω=nΩ
- If there are m such rows in parallel, the equivalent internal resistance Req is given by:
Req=Rinternal, one rowm=nm
4. Set Up the Equation for Maximum Power:
- To achieve maximum power, we set the equivalent internal resistance equal to the load resistance:
nm=10
5. Substitute for n:
- From the first equation n=24m. Substitute this into the equation for maximum power:
24mm=10
- This simplifies to:
24m2=10
6. Solve for m:
- Rearranging gives:
m2=2410=2.4
- Taking the square root:
m=√2.4≈1.55
- Since m must be a whole number, we can consider m=1 or m=2.
7. Calculate Corresponding n:
- If m=1:
n=241=24
- If m=2:
n=242=12
8. Evaluate the Two Cases:
- Case 1: m=1, n=24
- All cells in series: Req=24Ω (not suitable since it's greater than 10 ohms).
- Case 2: m=2, n=12
- Each row has 12 cells in series: Req=12Ω for each row.
- Total equivalent resistance for two rows in parallel:
Req=122=6Ω(which is less than 10 ohms)
9. Conclusion:
- The best configuration to achieve maximum power output across a load of 10 ohms is to connect 2 rows of 12 cells in series.
- The maximum power transfer theorem states that maximum power is transferred when the total internal resistance of the source (cells) equals the external load resistance.
- Therefore, we need to set the equivalent internal resistance of the cells equal to the load resistance (10 ohms).
- Let’s denote:
- m = number of rows (parallel connections)
- n = number of cells in each row (series connections)
- The total number of cells is given by:
m×n=24
- If n cells are connected in series, the total internal resistance for one row is:
Rinternal, one row=n×1Ω=nΩ
- If there are m such rows in parallel, the equivalent internal resistance Req is given by:
Req=Rinternal, one rowm=nm
- To achieve maximum power, we set the equivalent internal resistance equal to the load resistance:
nm=10
- From the first equation n=24m. Substitute this into the equation for maximum power:
24mm=10
- This simplifies to:
24m2=10
- Rearranging gives:
m2=2410=2.4
- Taking the square root:
m=√2.4≈1.55
- Since m must be a whole number, we can consider m=1 or m=2.
- If m=1:
n=241=24
- If m=2:
n=242=12
- Case 1: m=1, n=24
- All cells in series: Req=24Ω (not suitable since it's greater than 10 ohms).
- Case 2: m=2, n=12
- Each row has 12 cells in series: Req=12Ω for each row.
- Total equivalent resistance for two rows in parallel:
Req=122=6Ω(which is less than 10 ohms)
- The best configuration to achieve maximum power output across a load of 10 ohms is to connect 2 rows of 12 cells in series.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Solved Examples
13 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Exercise 7.1
22 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
A cell of emf 16V and internal resistant 4Ω can deliver maximum power to a load of resistance R where R is equal to
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionA voltmeter of resistance 998Ω is connected across a cell of emf 2 V and internal resistance 2Ω. Find the p.d. across the voltmeter, that across the terminals of the cell and percentage error in the reading of the voltmeter.
View SolutionIn the situation shown each cell has e.m.f. 4V and internal resistance 1Ω. The maximum power that can be delivered to the variable load resistance R is

View SolutionA resistance of 4Ω and a wire of length 5 meters and resistance 5Ω are joined in series and connected to a cell of e.m.f. 10V and internal resistance 1Ω. A parallel combination of two identical cells is balanced across 300cm of wire. The e.m.f. E of each cell is
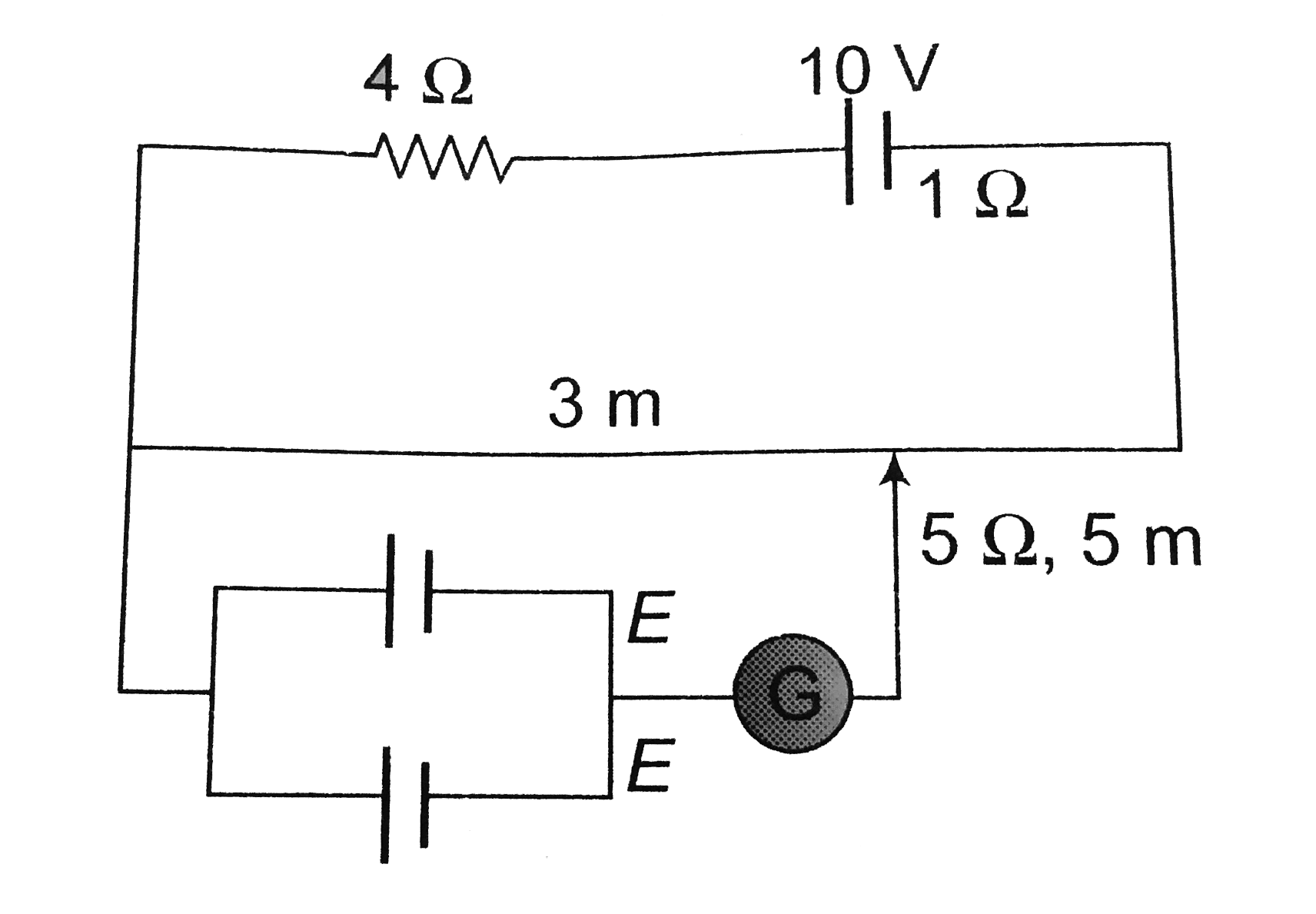
View SolutionFour equal resistance dissipated 5 W of power together when connected in series to a battery of negligible internal resistance . The total power dissipated in these resistance when connected in parallel across the same battery would be .
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionA capacitor of capacitance 1μF is connected in parallel with a resistance 10Ω and the combination is connected across the terminals of a battery of EMF 50 V and internal resistance 1Ω. The potential difference across the capacitor at steady state is (in Volt)
View Solutiontwo heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
View SolutionTwo cells having emf's of 10 V and 8 V, respectively, are connected in series with a resistance of 24Ω In the external circuit. Their internal resistances are 2Ω/V (proportional to their emf's). Find the current in the circuit

View Solution
