In the circuit shown in figure ,
a. find the current is each branch
b. find the potential difference Vab of point a relative to point b.
To solve the problem step-by-step, we will first find the current in each branch of the circuit and then calculate the potential difference Vab between points A and B.
Step 1: Identify the Circuit Components
- We have two batteries: a 10V battery and a 5V battery.
- The resistances are:
- R1=2Ω
- R2=3Ω
- R3=1Ω
- R4=4Ω
- R5=10Ω
Step 2: Assign Current Directions
- Let I1 be the current flowing through the branch with the 10V battery.
- Let I2 be the current flowing through the branch with the 5V battery.
- The total current flowing from point A to point B is I1+I2.
Step 3: Apply Kirchhoff's Voltage Law (KVL)
1. For the upper loop (A-D-C-B-A):
−I2⋅1−4I2+3I1−10=0
Rearranging gives:
5I2−5+3I1=0(Equation 1)
2. For the lower loop (D-E-F-C-D):
10I1+4I2−5−I2=0
Rearranging gives:
10I1+3I2=5(Equation 2)
Step 4: Solve the Equations
From Equation 1:
3I1=5−5I2⟹I1=5−5I23(Substituting into Equation 2)
Substituting I1 into Equation 2:
10(5−5I23)+3I2=5
Multiplying through by 3 to eliminate the fraction:
50−50I2+9I2=15
Combining like terms:
−41I2=−35⟹I2=3541≈0.85A
Now substitute I2 back into Equation 1 to find I1:
3I1=5−5⋅3541
Calculating:
3I1=5−17541=205−17541=3041
Thus,
I1=1041≈0.24A
Step 5: Calculate the Total Current
The total current flowing from A to B is:
Itotal=I1+I2=1041+3541=4541≈1.1A
Step 6: Calculate the Potential Difference Vab
Using the relation:
VA−VB=4I2−3I1
Substituting the values:
Vab=4⋅3541−3⋅1041
Calculating:
Vab=14041−3041=11041≈2.68V
Final Answers
- Current in each branch:
- I1≈0.24A
- I2≈0.85A
- Total current Itotal≈1.1A
- Potential difference Vab≈2.68V
- We have two batteries: a 10V battery and a 5V battery.
- The resistances are:
- R1=2Ω
- R2=3Ω
- R3=1Ω
- R4=4Ω
- R5=10Ω
- Let I1 be the current flowing through the branch with the 10V battery.
- Let I2 be the current flowing through the branch with the 5V battery.
- The total current flowing from point A to point B is I1+I2.
1. For the upper loop (A-D-C-B-A):
−I2⋅1−4I2+3I1−10=0
Rearranging gives:
5I2−5+3I1=0(Equation 1)
10I1+4I2−5−I2=0
Rearranging gives:
10I1+3I2=5(Equation 2)
From Equation 1:
3I1=5−5I2⟹I1=5−5I23(Substituting into Equation 2)
10(5−5I23)+3I2=5
Multiplying through by 3 to eliminate the fraction:
50−50I2+9I2=15
Combining like terms:
−41I2=−35⟹I2=3541≈0.85A
3I1=5−5⋅3541
Calculating:
3I1=5−17541=205−17541=3041
Thus,
I1=1041≈0.24A
The total current flowing from A to B is:
Itotal=I1+I2=1041+3541=4541≈1.1A
Using the relation:
VA−VB=4I2−3I1
Substituting the values:
Vab=4⋅3541−3⋅1041
Calculating:
Vab=14041−3041=11041≈2.68V
- Current in each branch:
- I1≈0.24A
- I2≈0.85A
- Total current Itotal≈1.1A
- Potential difference Vab≈2.68V
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Subjective
29 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Single Correct
72 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.1
28 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
Similar Questions
In the circuit shown in figure, find the current through the branch BD.
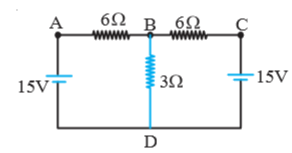
View SolutionIn the circuit shown in figure find Vab at 1s

View SolutionFind the current in each branches of the circuit.
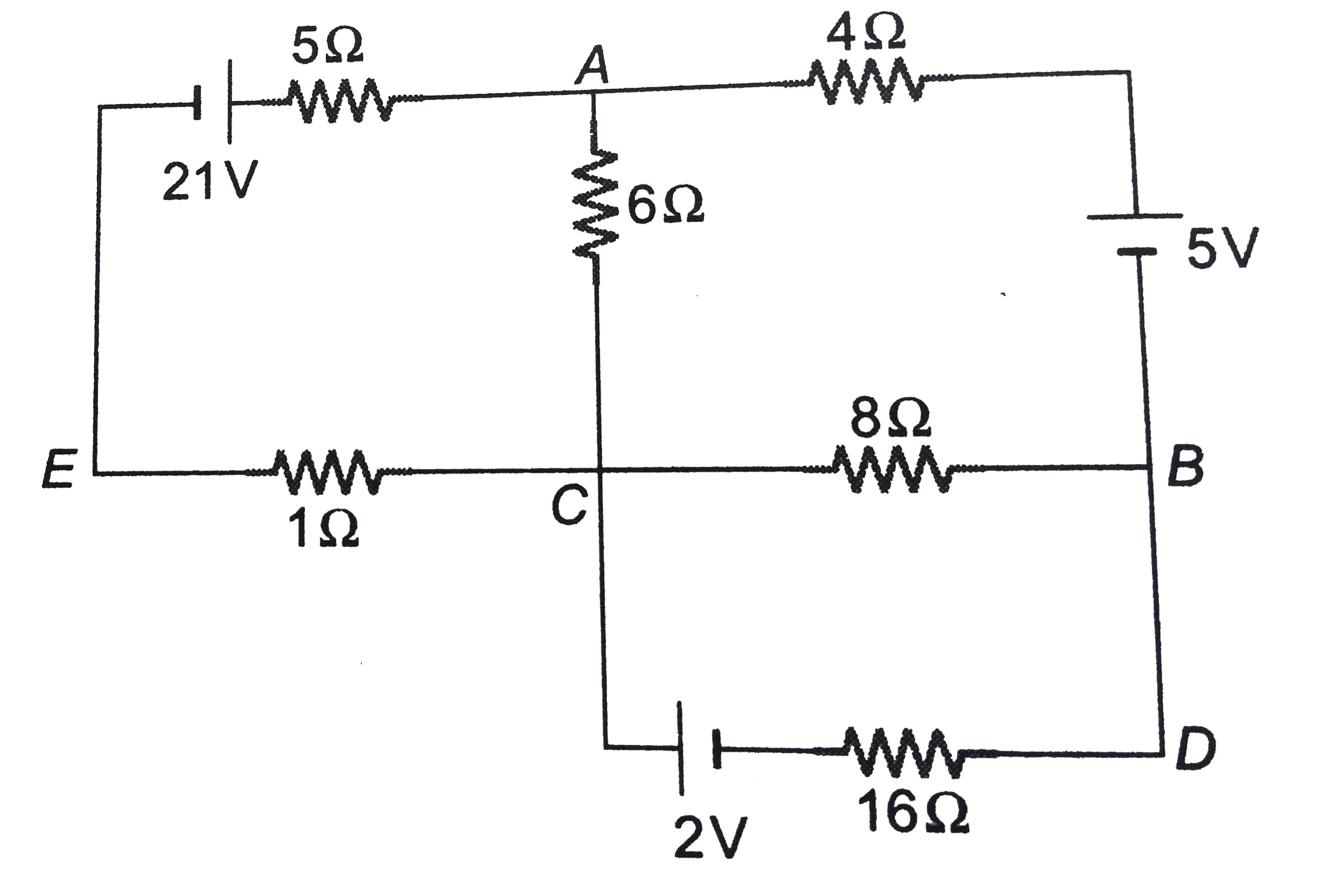
View SolutionFind theh potential difference between points a and b.
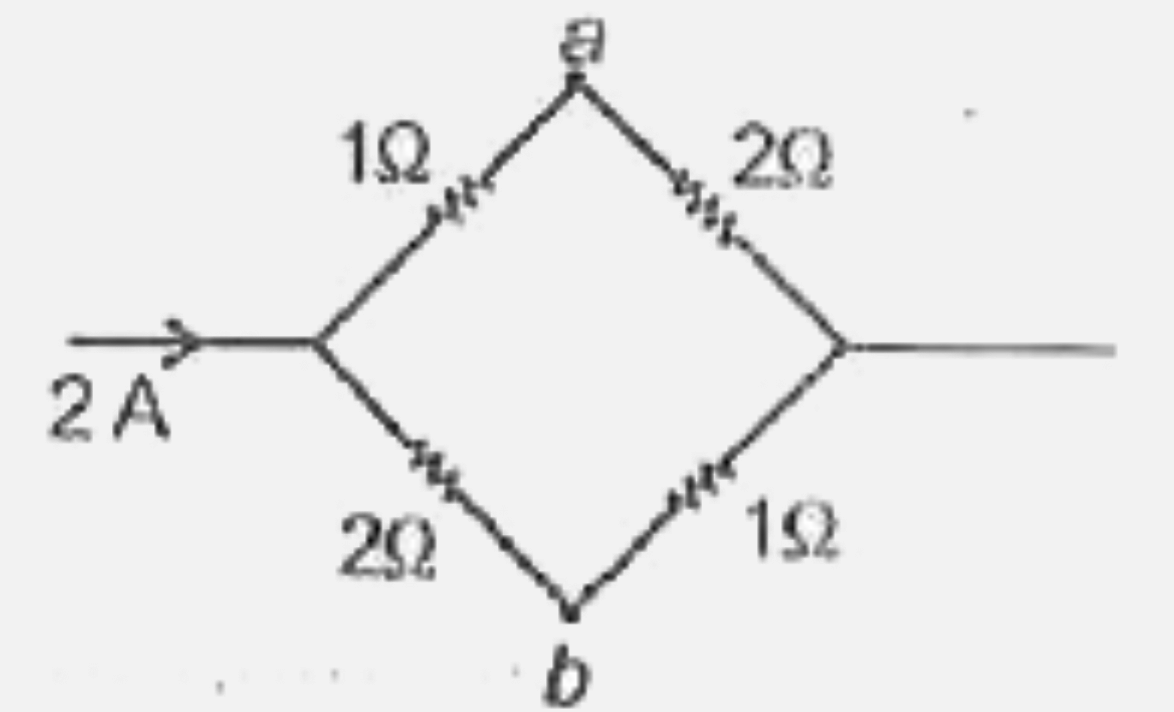
View SolutionFind the potential difference Va−Vbin the circutis shown in figure

View SolutionCalculate the value of the resistance R in the circuit shown in the figure so that the current in the circuit is 0.2 A. What would be the potential difference between points B and E?
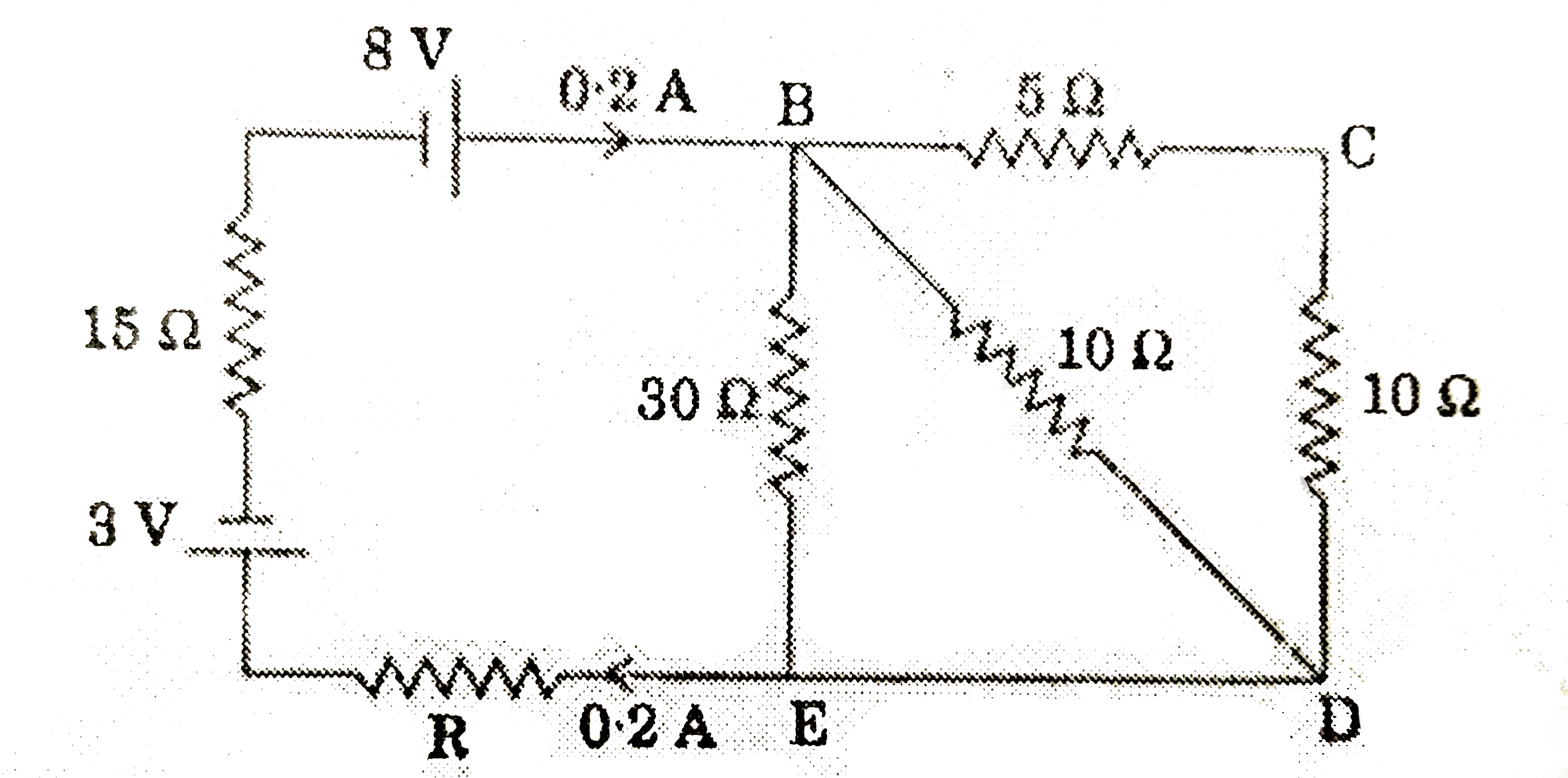
View SolutionCalculate the value of resistance R in the circuit shown in the figure so that the current in the circuits is 0.2A. What would be the potential difference between the points B and E ?
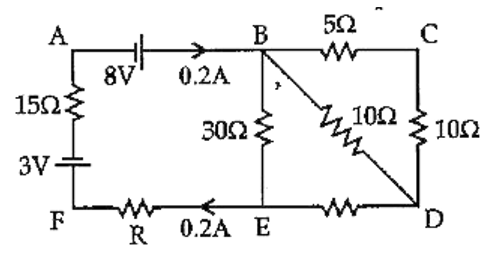
View SolutionFor the circuit in find the potential difference between points a and b.
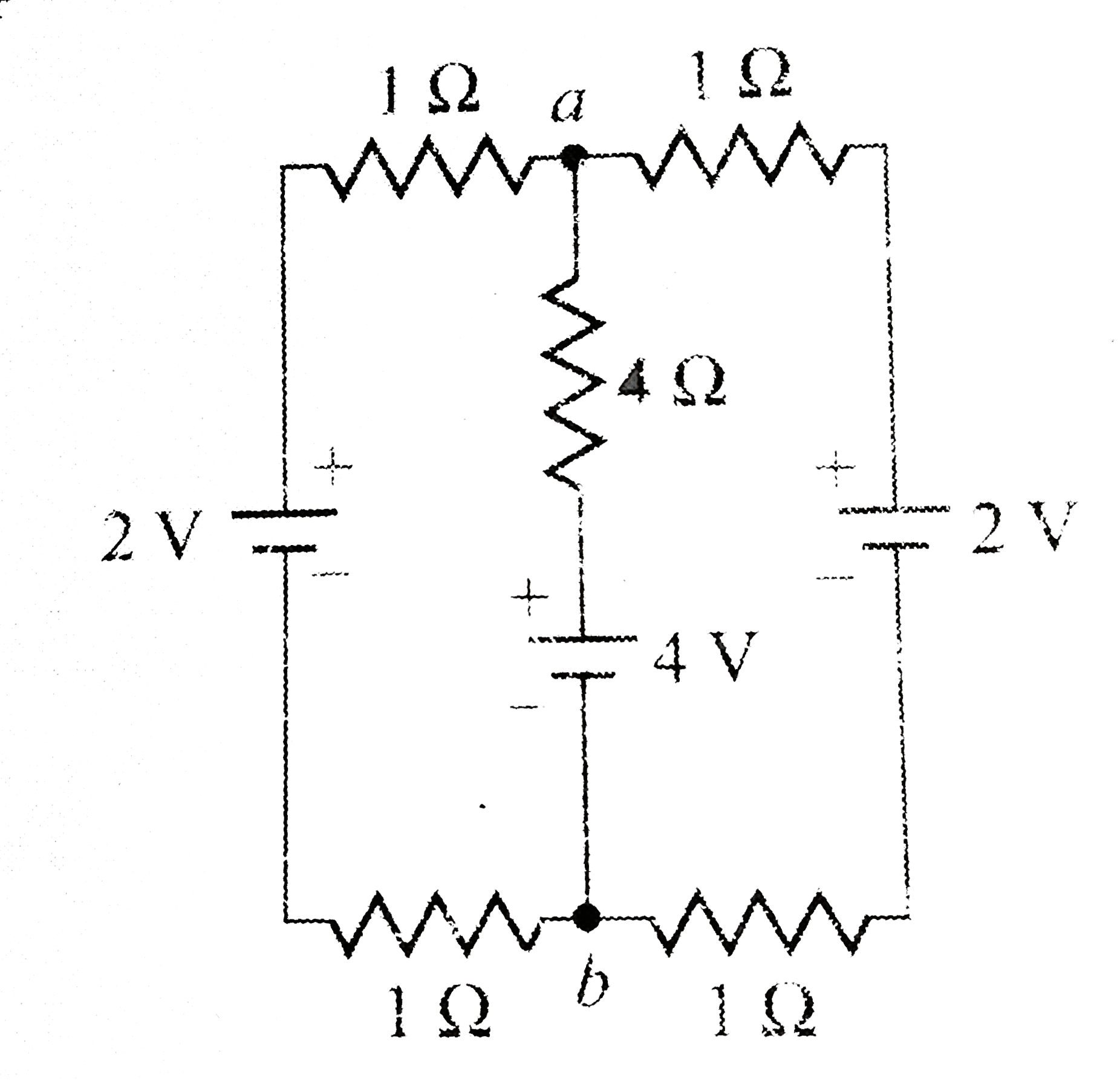
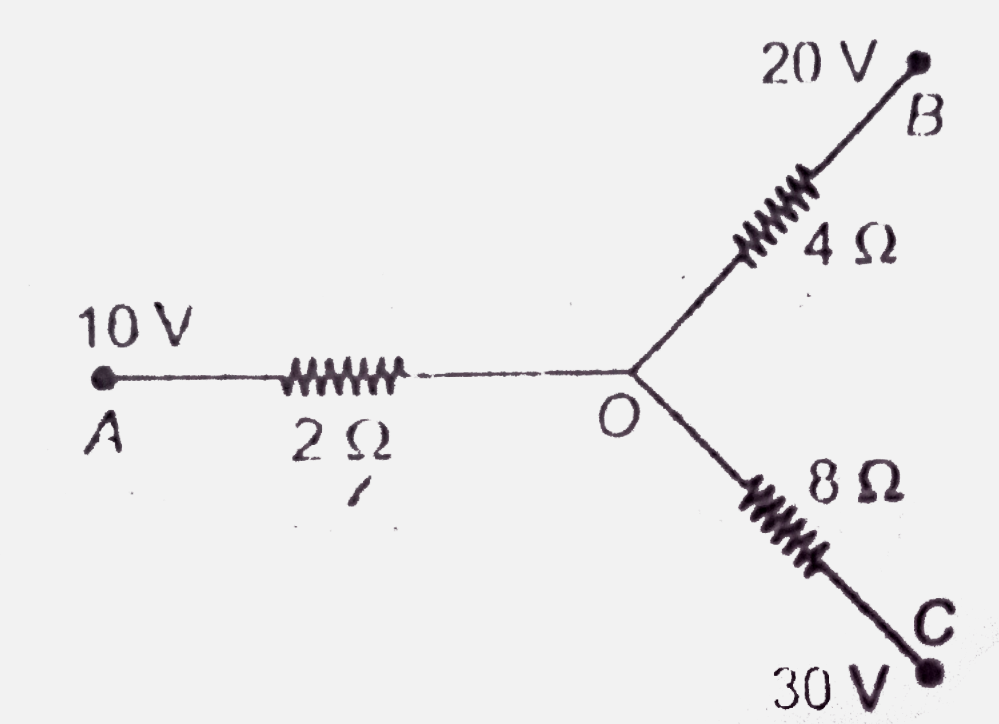
View SolutionConsider the circuit shown in the figure. Find the current in branch AO and OC . Potential of point A = 10 V of point B = 20 V and of C = 30 V.
View SolutionIn the circuit shown in the figure , no current flows through the 8Omega resistor, then the potential difference between points A and B(V_A - V_B) is
_PHY_E01_001_Q01.png)
View Solution
