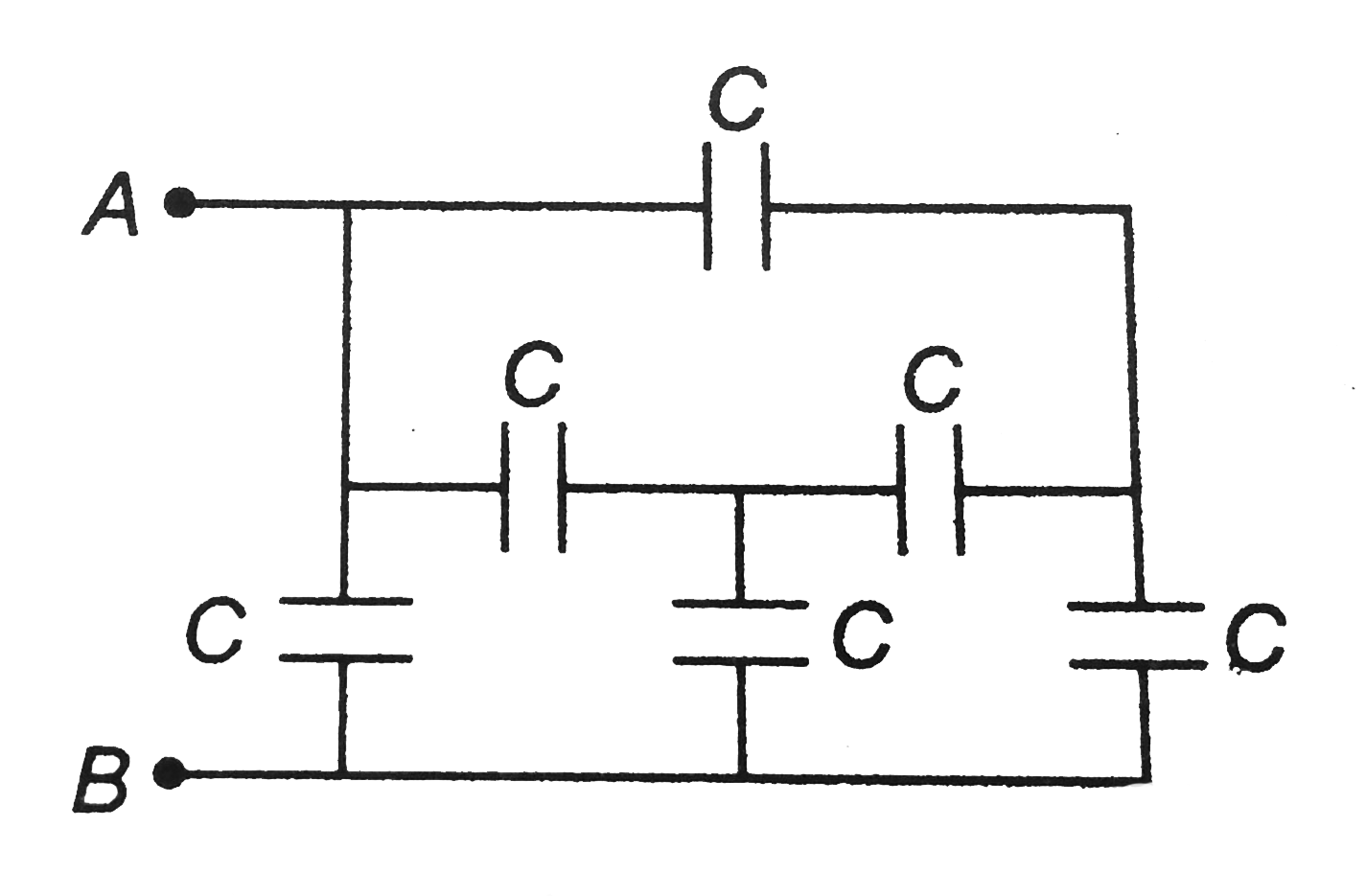
Six capacitors are arranged as shown in. Determine the equivalent capacitance between A and B.
To find the equivalent capacitance between points A and B for the given arrangement of six capacitors C1,C2,C3,C4,C5,C6 where each capacitor has a capacitance of C, we can follow these steps:
Step 1: Identify the Configuration
The capacitors are arranged in a way that forms a Wheatstone bridge configuration. In this arrangement, we can identify which capacitors are in series and which are in parallel.
Step 2: Simplify the Circuit
In a balanced Wheatstone bridge, we can ignore one of the branches. Here, we can ignore the capacitor C3 because it does not affect the overall capacitance between points A and B.
Step 3: Analyze the Remaining Capacitors
After ignoring C3, we have:
- Capacitors C1 and C6 in series.
- Capacitors C2 and C5 in series.
- Capacitor C4 is directly between points A and B.
Step 4: Calculate Series Capacitance
For capacitors in series, the equivalent capacitance Ceq is given by the formula:
1Ceq=1C1+1C6
Since C1=C and C6=C:
1Ceq1=1C+1C=2C⟹Ceq1=C2
Similarly, for capacitors C2 and C5:
1Ceq2=1C2+1C5=1C+1C=2C⟹Ceq2=C2
Step 5: Combine the Equivalent Capacitances
Now we have:
- Ceq1=C2 (from C1 and C6)
- Ceq2=C2 (from C2 and C5)
- C4=C (directly between A and B)
Now, these three capacitances Ceq1,Ceq2, and C4 are in parallel:
Ctotal=Ceq1+Ceq2+C4=C2+C2+C=C+C=2C
Final Answer
The equivalent capacitance between points A and B is:
Ceq=2C
The capacitors are arranged in a way that forms a Wheatstone bridge configuration. In this arrangement, we can identify which capacitors are in series and which are in parallel.
In a balanced Wheatstone bridge, we can ignore one of the branches. Here, we can ignore the capacitor C3 because it does not affect the overall capacitance between points A and B.
After ignoring C3, we have:
- Capacitors C1 and C6 in series.
- Capacitors C2 and C5 in series.
- Capacitor C4 is directly between points A and B.
For capacitors in series, the equivalent capacitance Ceq is given by the formula:
1Ceq=1C1+1C6
Since C1=C and C6=C:
1Ceq1=1C+1C=2C⟹Ceq1=C2
1Ceq2=1C2+1C5=1C+1C=2C⟹Ceq2=C2
Now we have:
- Ceq1=C2 (from C1 and C6)
- Ceq2=C2 (from C2 and C5)
- C4=C (directly between A and B)
Ctotal=Ceq1+Ceq2+C4=C2+C2+C=C+C=2C
The equivalent capacitance between points A and B is:
Ceq=2C
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Solved Examples
Explore 10 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Exercise 4.1
Explore 13 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
Similar Questions
Find the equivalent capacitance between C and B.
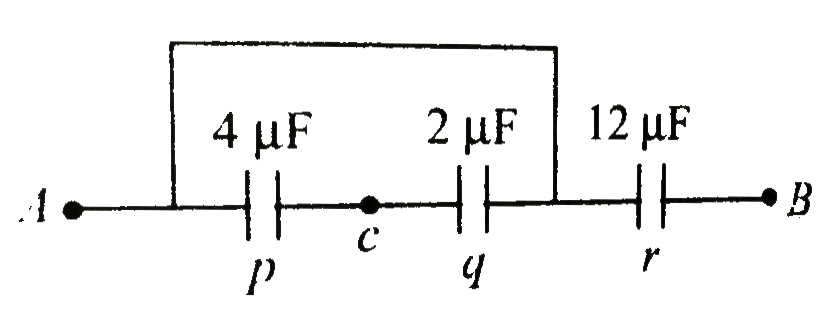
View SolutionIf each capacitor has capacitance C, then equivalent capacitance between A and B is

View SolutionEach capacitor has cpacitance C.
 .
.
The equivalent capacitance between 4 and 5 is .
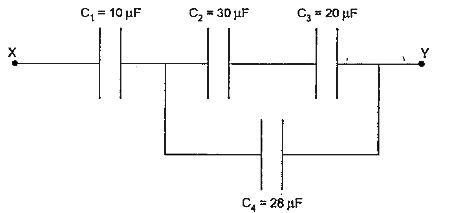
View SolutionFour capacitors, C1C2C3andC4 are connected as shown in figure below. Calculate • equivalent capacitance of the circuit between points X and Y.
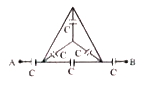
View SolutionSix identical capacitors of each capacitance .C. are arranged as shown in fig .The equivalent capacitance between A and B is KC8 . The value of .K. is ..........
View SolutionSix equal capacitors each of capacitance C are connected as shown in the figure. The equivalent capacitance between points A and B is
View SolutionIn the accompanying diagram , if C1=3μF,C2=6μF,C3=9μF,C4=12μF,C5=15μFandC6=18μF , then the equivalent capacitor between the ends A and B is
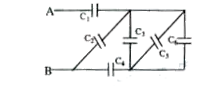
View SolutionFour capacitors C1=8μF,
C2=2μf,C3=6μF, and C4=6,μF are arranged as shown in. Find the charge on all the capacitors in the circuit.
 .
.
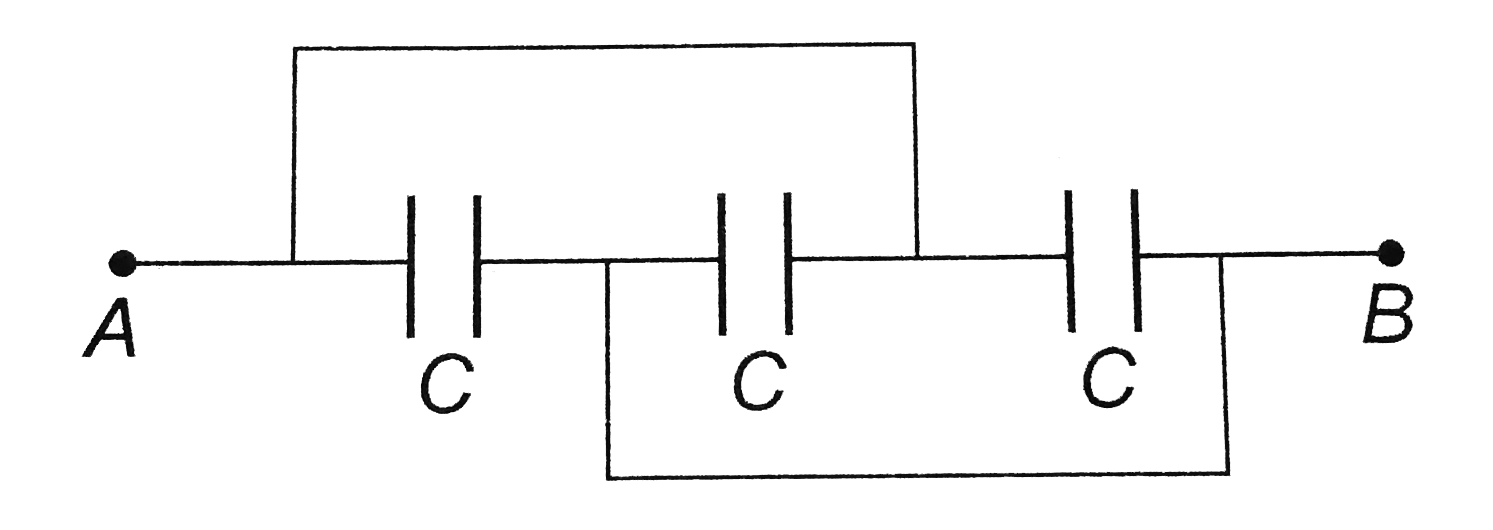
View SolutionThree equal capacitors, each with capacitance C are connected as shown in figure. Then the equivalent capacitance between A and B is
View SolutionA number of capacitors, each euqal capacitance C, are arranged as shown in . The equialent capacitance between A and B is
 .
.
View Solution
