A spherical drop of capacitance 12μF is broken into eight drops of equal radius. What is the capacitance of each small drop in μF?
The correct Answer is:6
To solve the problem, we need to find the capacitance of each small drop after a spherical drop of capacitance 12 µF is divided into eight smaller drops of equal radius.
1. Understand the relationship between capacitance and radius:
The capacitance C of a spherical conductor is given by the formula:
C=4πϵ0R
where R is the radius of the sphere.
2. Given capacitance of the large drop:
We know that the capacitance of the large drop is:
C=12μF
3. Volume conservation:
When the large drop is broken into 8 smaller drops, the total volume remains constant. The volume V of a sphere is given by:
V=43πR3
Let R be the radius of the large drop and r be the radius of each small drop. The volume of the large drop is:
Vlarge=43πR3
The volume of one small drop is:
Vsmall=43πr3
Since there are 8 small drops, the total volume of the small drops is:
Vtotal=8×Vsmall=8×43πr3
4. Setting volumes equal:
Since the volume is conserved:
43πR3=8×43πr3
We can cancel 43π from both sides:
R3=8r3
5. Solving for the radius of the small drops:
Taking the cube root of both sides gives:
R=2r
6. Finding the capacitance of the small drop:
The capacitance of each small drop can be calculated using the radius r:
Csmall=4πϵ0r
Since R=2r, we can substitute r=R2:
Csmall=4πϵ0(R2)=2⋅4πϵ0R
Now, substituting 4πϵ0R=12μF:
Csmall=2⋅12μF=6μF
Final Answer:
The capacitance of each small drop is 6μF.
---
The capacitance C of a spherical conductor is given by the formula:
C=4πϵ0R
where R is the radius of the sphere.
We know that the capacitance of the large drop is:
C=12μF
When the large drop is broken into 8 smaller drops, the total volume remains constant. The volume V of a sphere is given by:
V=43πR3
Let R be the radius of the large drop and r be the radius of each small drop. The volume of the large drop is:
Vlarge=43πR3
The volume of one small drop is:
Vsmall=43πr3
Since there are 8 small drops, the total volume of the small drops is:
Vtotal=8×Vsmall=8×43πr3
Since the volume is conserved:
43πR3=8×43πr3
We can cancel 43π from both sides:
R3=8r3
Taking the cube root of both sides gives:
R=2r
The capacitance of each small drop can be calculated using the radius r:
Csmall=4πϵ0r
Since R=2r, we can substitute r=R2:
Csmall=4πϵ0(R2)=2⋅4πϵ0R
Now, substituting 4πϵ0R=12μF:
Csmall=2⋅12μF=6μF
The capacitance of each small drop is 6μF.
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Comprhension
Explore 35 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
Similar Questions
A spherical drop of capacitance 1μF is broken into eight drop of equal radius. Then, the capacitance of each small drop is
View Solution1000 small water drops each of capacitance C join togethter to form one large spherical drop. The capacitance of bigge sphere is
View SolutionA spherical liquid drop of radius R is divided into eight equal droplets. If the surface tension is T, then the work done in this process will be
View SolutionThe effective capacitence in μF in between A and B will be
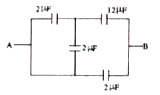
View SolutionA parallel plate capacitor 'A' of capacitance 1μF is charged to a potential drop 100 volt and then disconnected form the battery. Now the capacitor 'A' is completely filled with a dielectric slap of dielectric constant k=4. Another parallel plate capacitor 'B' of capacitance 2μF is charged to a potential drop 20 volt and then disconnected from the battery. Now the two capacitors 'A' and 'B' are connected with each other with opposite polarities. Then the heat dissipated after connecting the capacitors is
View SolutionA certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
View SolutionA capacitor of capacitor of capacitance 2.0μF is charge to a potential diffrence of 12V It is then connected of uncharged capacitor of capacitance 4.0μF as shown in figure . Find (a ) the charge on each of the two capacitors after the connection, (b ) the electrostatic energy stored in each of the two capacitors.

View SolutionThree capacitors 2μF,3μFand6μF are joined with each other. What is the minimum effective capacitance?
View SolutionThe minimum number of condensers each capacitance of 2μF, in order to obtain result capacitance of 5μF will be
View SolutionThe potential of a large liquid drop when eight liquid drops are combined is 20 V. Then, the potential of each single drop was
View Solution
