Two point charges are located on the x - axis : q1=−e at x=0 and q2=+e at x=a.
The work done by an external force to bring a third point charge q3=+e from infinity to x=2a is.
e24πε0a
e28πε0a
−e28πε0a
−e24πε0a
The correct Answer is:B
To solve the problem of finding the work done by an external force to bring a third point charge q3=+e from infinity to x=2a, we will follow these steps:
Step 1: Understand the System
We have two point charges:
- q1=−e located at x=0
- q2=+e located at x=a
We need to bring a third charge q3=+e from infinity to the position x=2a.
Step 2: Calculate Initial Potential Energy
The initial potential energy Ui of the system, which consists of q1 and q2, is given by the formula:
Ui=kq1q2r12
where k is Coulomb's constant, r12 is the distance between q1 and q2, which is a.
Substituting the values:
Ui=k(−e)(e)a=−ke2a
Step 3: Calculate Final Potential Energy
Now, we need to calculate the final potential energy Uf of the system when q3 is added at x=2a. The final potential energy includes contributions from all three charges:
Uf=kq1q2a+kq2q3a+kq1q32a
Calculating each term:
1. kq1q2a=−ke2a
2. kq2q3a=k(e)(e)a=ke2a
3. kq1q32a=k(−e)(e)2a=−ke22a
Adding these contributions together:
Uf=−ke2a+ke2a−ke22a
The first two terms cancel each other out:
Uf=−ke22a
Step 4: Calculate Work Done
The work done W by the external force is equal to the change in potential energy:
W=Uf−Ui
Substituting the values we found:
W=(−ke22a)−(−ke2a)
This simplifies to:
W=−ke22a+ke2a=ke22a
Step 5: Substitute the Value of k
Using k=14πϵ0:
W=12⋅e24πϵ0a=e28πϵ0a
Final Answer
The work done by the external force to bring the charge q3 from infinity to x=2a is:
W=e28πϵ0a
We have two point charges:
- q1=−e located at x=0
- q2=+e located at x=a
The initial potential energy Ui of the system, which consists of q1 and q2, is given by the formula:
Ui=kq1q2r12
where k is Coulomb's constant, r12 is the distance between q1 and q2, which is a.
Ui=k(−e)(e)a=−ke2a
Now, we need to calculate the final potential energy Uf of the system when q3 is added at x=2a. The final potential energy includes contributions from all three charges:
Uf=kq1q2a+kq2q3a+kq1q32a
1. kq1q2a=−ke2a
2. kq2q3a=k(e)(e)a=ke2a
3. kq1q32a=k(−e)(e)2a=−ke22a
Uf=−ke2a+ke2a−ke22a
The first two terms cancel each other out:
Uf=−ke22a
The work done W by the external force is equal to the change in potential energy:
W=Uf−Ui
Substituting the values we found:
W=(−ke22a)−(−ke2a)
This simplifies to:
W=−ke22a+ke2a=ke22a
Using k=14πϵ0:
W=12⋅e24πϵ0a=e28πϵ0a
The work done by the external force to bring the charge q3 from infinity to x=2a is:
W=e28πϵ0a
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Integer
5 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.1
14 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Two points charges are located on the x-axis, q1=−1μC at x=0andq2=+1μc at x=1m.
a. Find the work that must be done by an external force to bring a third point charge q3=+1μC from infinity to x=2m.
b. Find the total potential energy of the system of three charges.
View SolutionTwo points charges are located on the x-axis, q1=−1μC at x=0andq2=+1μc at x=1m.
a. Find the work that must be done by an external force to bring a third point charge q3=+1μC from infinity to x=2m.
b. Find the total potential energy of the system of three charges.
View SolutionTwo point charges are located on the x - axis : q1=−e at x=0 and q2=+e at x=a. A third charge q3=+e is brought to x=2a.
The total potential energy of the system of three charges.
View SolutionA charge Q is placed at the origin. The electric potential due to this charge at a given point in space is V. The work done by an external force in bringing another charge q from infinity up to the point is
View SolutionFind the work done by some external force in moving a charge q=2μC from infinity to a point where electric potential is 104 V.
View SolutionFind the work done by some external force in moving a charge q=4μC from infinity to a point, where electric potential is 104V
View SolutionTwo point charges Q and -Q/4 are separated by a distance x.

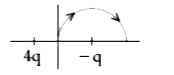
View SolutionA two point charges 4q and -q are fixed on the x - axis x=−d2andx=d2 , respectively. If a third point charge 'q' is taken from the origin to x = d along the semicircle as shown in the figure, the energy of the charge will
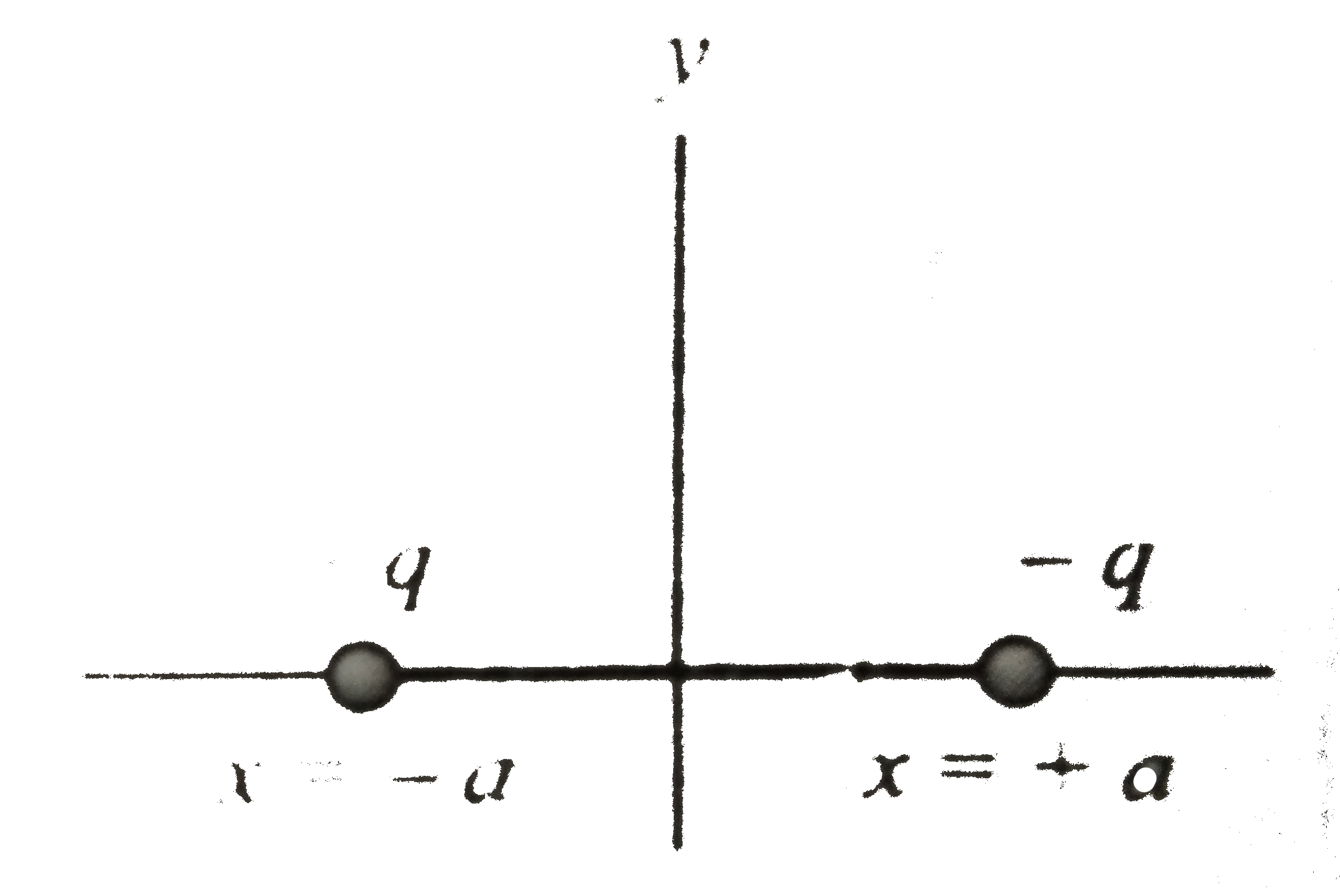
View SolutionTwo point charge ±q are placed on the axis at x=−a and x=+a, as shown in fig.
(i) Plot the variation of E along the x-axis.
(ii) Plot the variation of E along the y-axis.
View SolutionThe charges - q, Q, -q are placed along x-axis at x = 0, x = a and x = 2a. If the potential energy of the system is zero, then Q:q is
View Solution
