There is an infinite straight chain of alternating charges q and −q . The distance between the neighbouring charges is equal to a. Find the interaction energy of each charge with all the others.
Instruction . Make use of the expansion of In (1+α) in a power series in α.
−2q4πε0a
2q2loge24πε0a
−2q2loge24πε0a
none of these.
The correct Answer is:c
To find the interaction energy of each charge in an infinite straight chain of alternating charges +q and −q, we can follow these steps:
Step 1: Understanding the Configuration
We have an infinite chain of charges alternating between +q and −q, with a distance a between neighboring charges. The charges can be represented as follows:
…,+q,−q,+q,−q,+q,−q,…
Step 2: Calculating the Interaction Energy
The interaction energy U of a charge due to another charge is given by the formula:
U=kq1q2r
where k is Coulomb's constant, q1 and q2 are the magnitudes of the charges, and r is the distance between them.
For a charge +q (let's consider the first charge in the chain), the interaction energy with the neighboring charges can be calculated as follows:
1. First Neighbor (−q at distance a):
U1=kq⋅(−q)a=−kq2a
2. Second Neighbor (+q at distance 2a):
U2=kq⋅q2a=kq22a
3. Third Neighbor (−q at distance 3a):
U3=kq⋅(−q)3a=−kq23a
4. Fourth Neighbor (+q at distance 4a):
U4=kq⋅q4a=kq24a
Continuing this pattern, we can express the total interaction energy U for the charge +q as:
U=U1+U2+U3+U4+…
U=−kq2a+kq22a−kq23a+kq24a−…
Step 3: Factoring Out Common Terms
We can factor out kq2a:
U=kq2a(−1+12−13+14−…)
Step 4: Recognizing the Series
The series inside the parentheses is an alternating series:
S=−1+12−13+14−…
This series can be related to the logarithmic expansion:
log(1+x)=x−x22+x33−x44+…
For x=1:
log(2)=1−12+13−14+…
Thus, we can write:
S=−log(2)
Step 5: Final Expression for Interaction Energy
Substituting S back into the expression for U:
U=kq2a(−log(2))
Since k=14πϵ0:
U=−q2log(2)4πϵ0a
Step 6: Considering Both Sides of the Charge
Since the interaction energy is symmetric, we need to consider both sides of the charge:
Utotal=2U=−2q2log(2)4πϵ0a
Final Result
Thus, the total interaction energy of each charge with all the others is:
U=−q2log(2)2πϵ0a
---
We have an infinite chain of charges alternating between +q and −q, with a distance a between neighboring charges. The charges can be represented as follows:
…,+q,−q,+q,−q,+q,−q,…
The interaction energy U of a charge due to another charge is given by the formula:
U=kq1q2r
where k is Coulomb's constant, q1 and q2 are the magnitudes of the charges, and r is the distance between them.
U1=kq⋅(−q)a=−kq2a
U2=kq⋅q2a=kq22a
U3=kq⋅(−q)3a=−kq23a
U4=kq⋅q4a=kq24a
U=U1+U2+U3+U4+…
U=−kq2a+kq22a−kq23a+kq24a−…
We can factor out kq2a:
U=kq2a(−1+12−13+14−…)
The series inside the parentheses is an alternating series:
S=−1+12−13+14−…
This series can be related to the logarithmic expansion:
log(1+x)=x−x22+x33−x44+…
For x=1:
log(2)=1−12+13−14+…
Thus, we can write:
S=−log(2)
Substituting S back into the expression for U:
U=kq2a(−log(2))
Since k=14πϵ0:
U=−q2log(2)4πϵ0a
Since the interaction energy is symmetric, we need to consider both sides of the charge:
Utotal=2U=−2q2log(2)4πϵ0a
Thus, the total interaction energy of each charge with all the others is:
U=−q2log(2)2πϵ0a
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Multiple Correct
10 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension
31 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Subjective
28 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Two equal charges q are placed at a distance of 2a and a third charge −2q is placed at the midpoint. The potential energy of the system is
View SolutionTwo conducting plates A and B are placed parallel to each other. A is given a charge. Q1 and B a charge Q2. Find the distribution of charges on the four surface.
View SolutionFind the potential energy of a charge q0 placed at the centre of regular hexagon of side a, if charge q is placed at each vertex of regular hexagon ?
View SolutionTwo charges of equal magnitudes and at a distance r exert a force F on each other. If the charges are halved and distance between them is doubled, then the new force acting on each charge is
View SolutionCharges−q,Q,and−q are placed at an equal distance on a straight liner. If the total potential energy of the system of three charges is zero, then find the ratio Q/q.
 .
.
View SolutionThree identical dipoles with charges q and −q, and separation A between the charges, are placed at the corners of an equilateral triangle of side D as shown in (Fig. 3.123). Find the interaction energy of the system (a<<d).
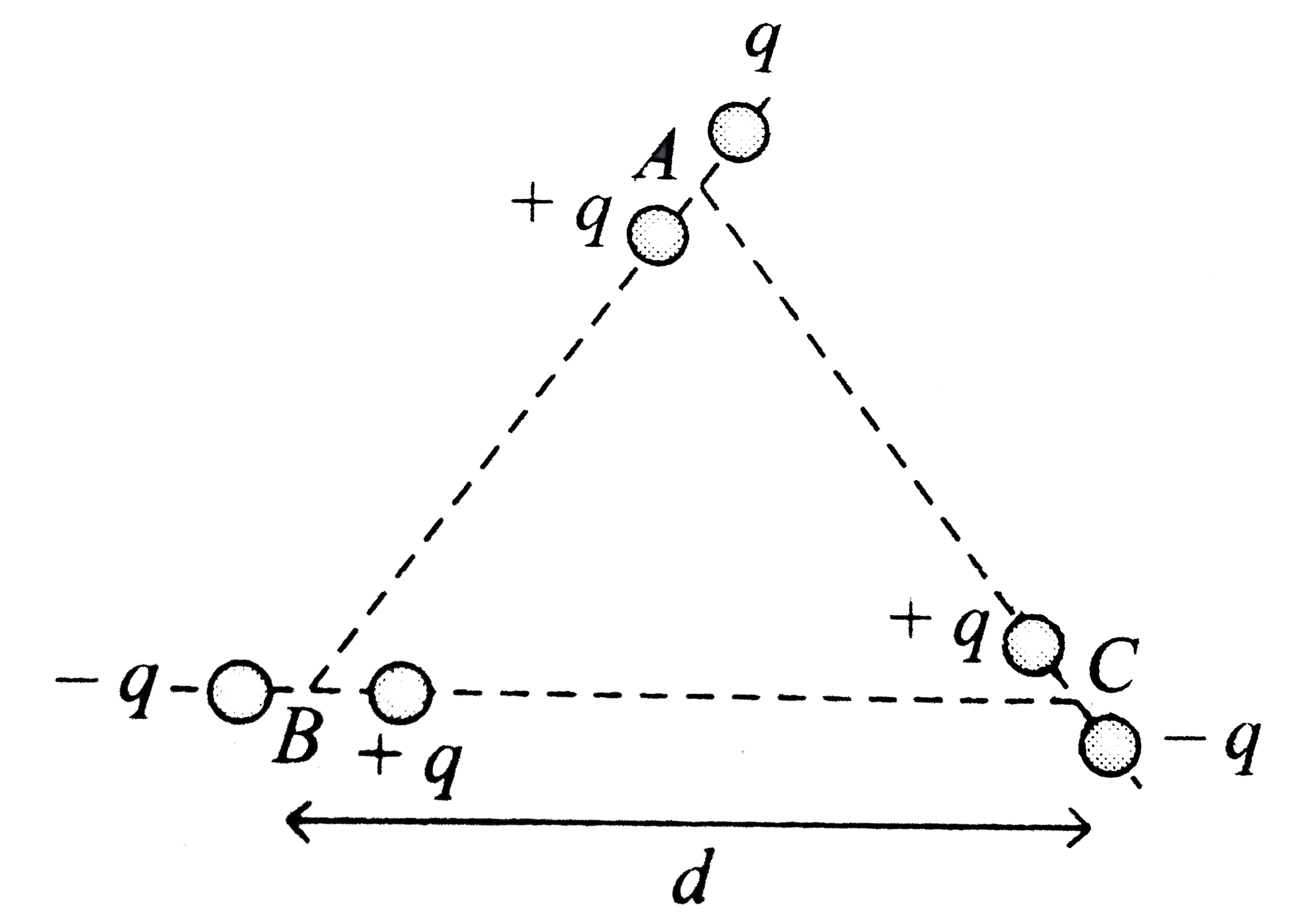 .
.
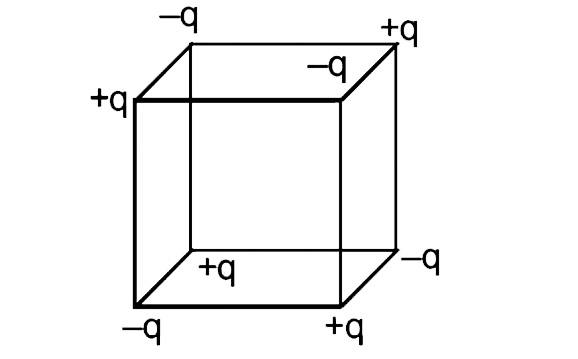
View SolutionCharges +q and −q are located at the corners of a cube of side as show in the figure. Find the work done to separate the charges to infinite distance
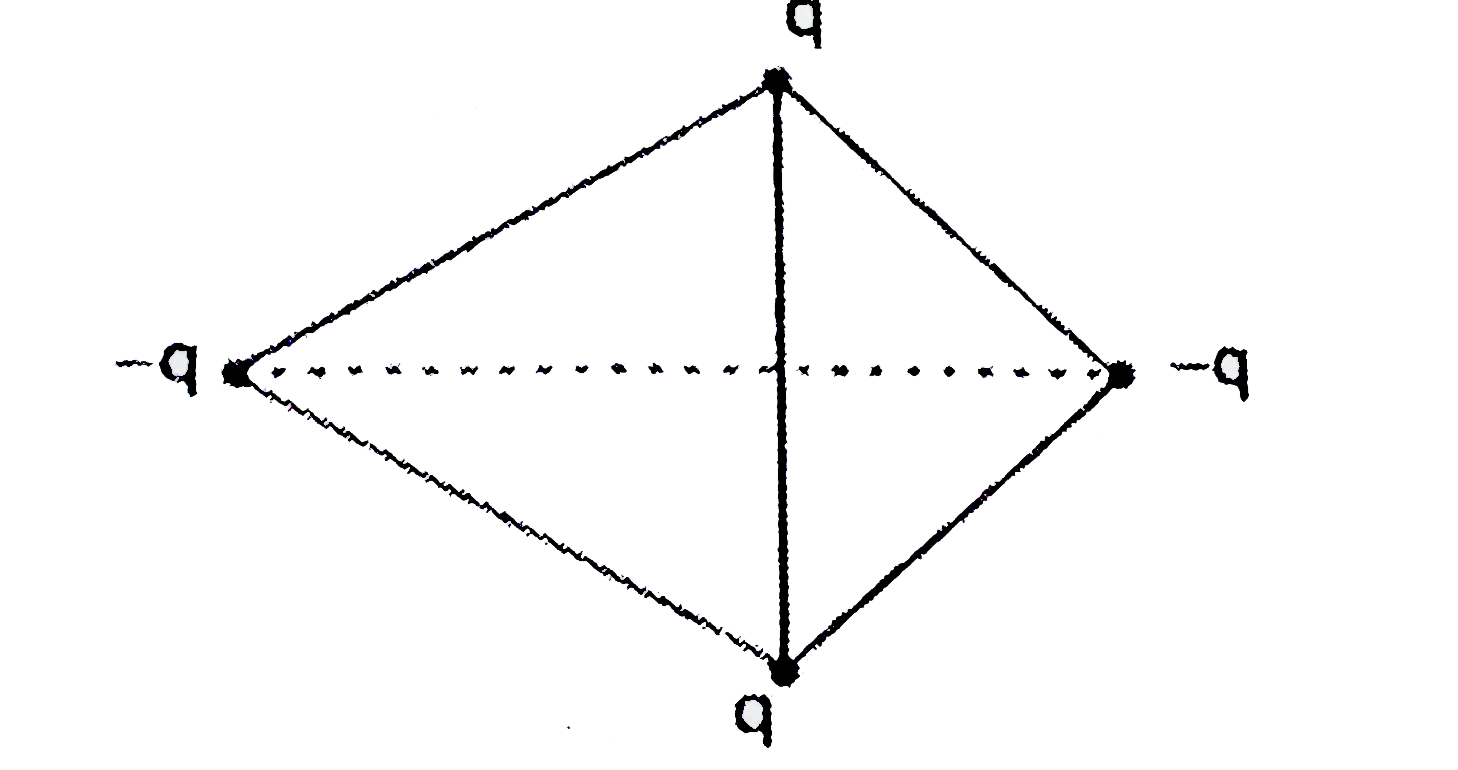
View SolutionFour small point charges (each of equal magnitude q) are placed at four corners of a regular tetrahedron of side a. find out potential energy of charge system
View SolutionThree equal charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out force acting on one of the charge due to other two charges ?
View SolutionTwo point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View Solution
