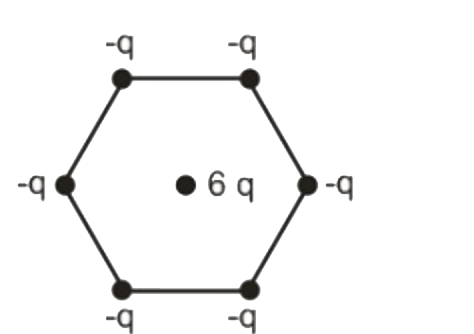
Find the potential energy of a charge q0 placed at the centre of regular hexagon of side a, if charge q is placed at each vertex of regular hexagon ?
The correct Answer is:6Kqq0a
To find the potential energy of a charge q0 placed at the center of a regular hexagon with charge q at each vertex, we can follow these steps:
Step 1: Understand the Geometry of the Hexagon
A regular hexagon has six equal sides. If the side length is a, the distance from the center of the hexagon to each vertex (where charge q is placed) can be determined. For a regular hexagon, this distance is equal to a.
Step 2: Identify the Charges and Their Positions
We have:
- Charge q0 at the center of the hexagon.
- Charge q at each of the six vertices.
Step 3: Use the Formula for Electric Potential Energy
The potential energy U due to a point charge is given by the formula:
U=kq1q2r
where:
- k is Coulomb's constant,
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
Step 4: Calculate the Potential Energy Contribution from Each Vertex Charge
Since all vertex charges are at the same distance r=a from the charge q0, the potential energy contributed by one charge q at a vertex is:
Usingle=kq0qa
Step 5: Calculate Total Potential Energy from All Vertex Charges
Since there are six vertex charges, the total potential energy Utotal is:
Utotal=6×Usingle=6(kq0qa)
Thus, we can write:
Utotal=6kq0qa
Final Answer
The potential energy of the charge q0 placed at the center of the regular hexagon is:
U=6kq0qa
---
A regular hexagon has six equal sides. If the side length is a, the distance from the center of the hexagon to each vertex (where charge q is placed) can be determined. For a regular hexagon, this distance is equal to a.
We have:
- Charge q0 at the center of the hexagon.
- Charge q at each of the six vertices.
The potential energy U due to a point charge is given by the formula:
U=kq1q2r
where:
- k is Coulomb's constant,
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
Since all vertex charges are at the same distance r=a from the charge q0, the potential energy contributed by one charge q at a vertex is:
Usingle=kq0qa
Since there are six vertex charges, the total potential energy Utotal is:
Utotal=6×Usingle=6(kq0qa)
Thus, we can write:
Utotal=6kq0qa
The potential energy of the charge q0 placed at the center of the regular hexagon is:
U=6kq0qa
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (E)
Explore 2 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (F)
Explore 4 Videos
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Exercise-1 Section (C)
Explore 14 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
Knowledge Check
Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
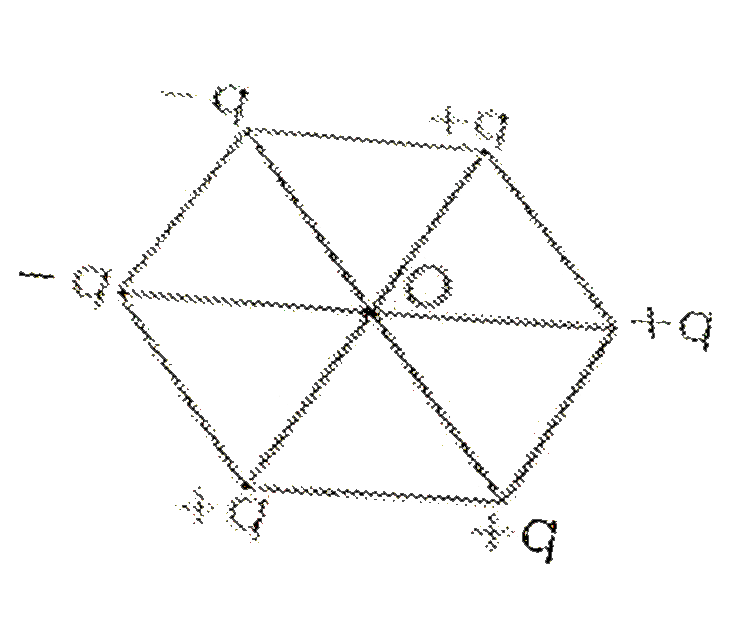
Find the magnitude of electric field at the centre of regular hexagon.A−qB−q6C+1.83qD−1.83q
Five equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is
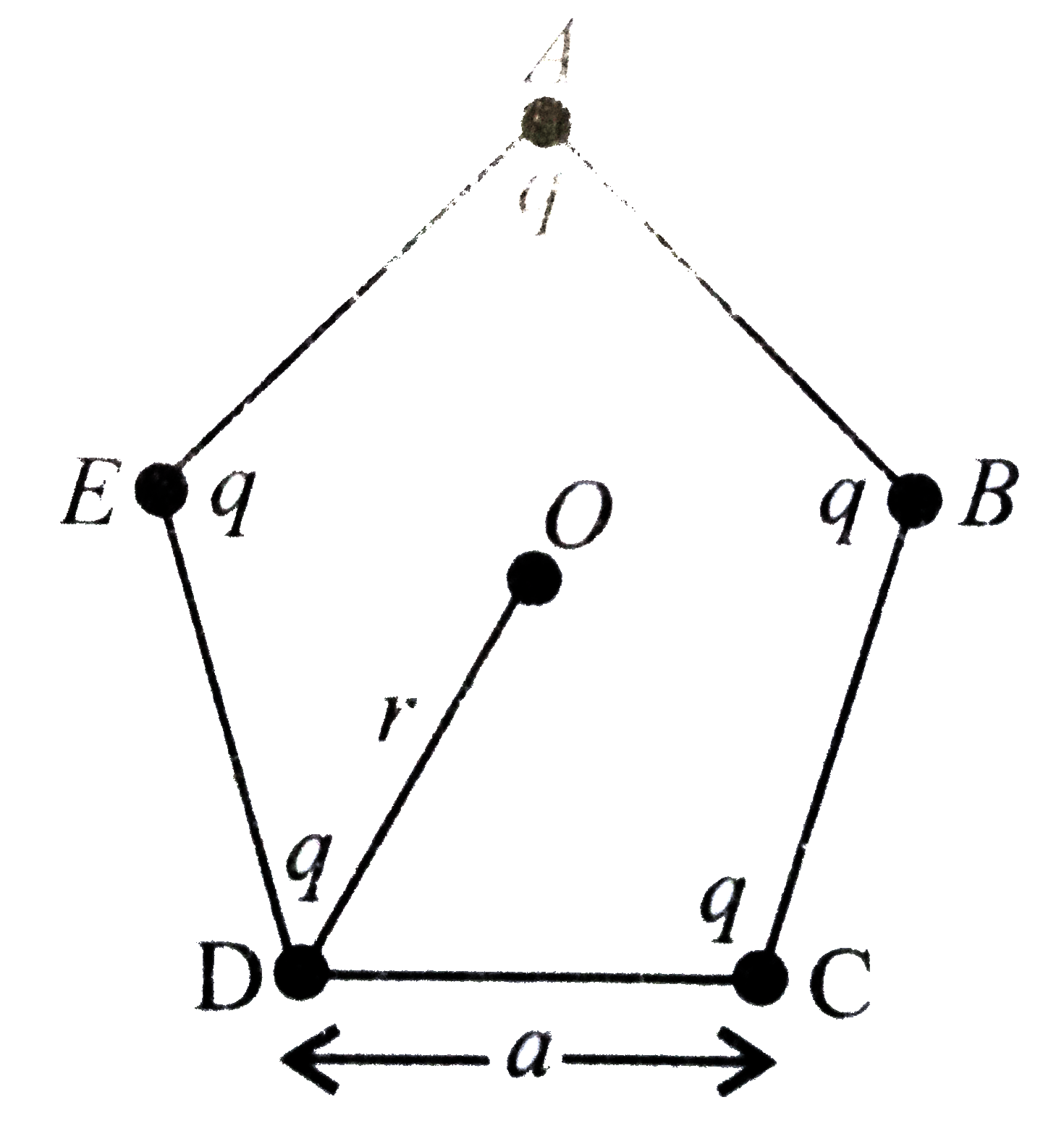
View SolutionFive charges, q each are placed at the coreners of a regular pentagone of side.
(a) (i) What will be the electric field at O, the centre of the pentagon ?
(ii) What will be the electric field 0 if the charge from one of the corners (say A) is removed ?
(iii) What will be the electric field at 0 if the charge q at A is replaced by −q ?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its coreners ?
View SolutionSix negative equal charge are placed at the vertical of a regular hexagon . 6q charge is placed at the centre of the hexagon . Find the electric dipole moment of the system.
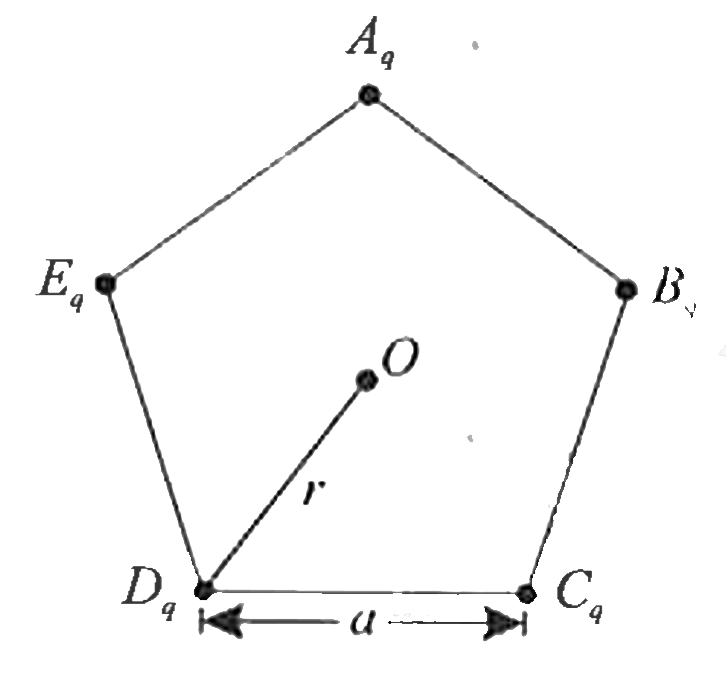
View SolutionFive point charges each of charge +q are placed on five vertices of a regular hexagon of side h as shown in the figure. Then
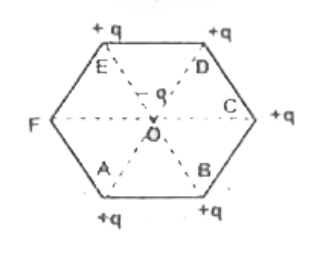
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionA point charge +Q is placed at the centroid of an equilateral triangle. When a second charge +Q is placed at a vertex of the triangle, the magnitude of the electrostatic force on the central charge is 8 N. The magnitude of the net force on the central charge when a third charge +Q is placed at another vertex of the triangle is
View SolutionFour identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
View Solution

