Two circular loops of radii 0.05 and 0.09m, respectively, are put such that their axes coincide and their centers are 0.12m apart. A charge of 10−6C is spread uniformly on each loop. Find the potential difference between the centers of the loops.
To find the potential difference between the centers of two circular loops with given parameters, we can follow these steps:
Step 1: Understand the Problem
We have two circular loops with radii r1=0.05m and r2=0.09m. The distance between their centers is x=0.12m. Each loop has a uniform charge of Q=10−6C. We need to find the potential difference between the centers of the two loops.
Step 2: Calculate the Potential at Center C1
The potential VC1 at the center of the first loop (with radius r1) due to its own charge is given by:
VC1=k⋅Q⋅⎛⎜
⎜⎝1r1+1√r22+x2⎞⎟
⎟⎠
Where k=9×109N⋅m2/C2.
Substituting the values:
- r1=0.05m
- r2=0.09m
- x=0.12m
Calculating VC1:
VC1=9×109⋅10−6⋅(10.05+1√(0.09)2+(0.12)2)
Calculating √(0.09)2+(0.12)2:
√0.0081+0.0144=√0.0225=0.15m
Now substituting back:
VC1=9×109⋅10−6⋅(10.05+10.15)
Calculating 10.05=20 and 10.15≈6.67:
VC1=9×109⋅10−6⋅(20+6.67)=9×109⋅10−6⋅26.67
VC1=9×26.67≈240V
Step 3: Calculate the Potential at Center C2
Similarly, the potential VC2 at the center of the second loop (with radius r2) is given by:
VC2=k⋅Q⋅⎛⎜
⎜⎝1r2+1√r21+x2⎞⎟
⎟⎠
Calculating VC2:
VC2=9×109⋅10−6⋅(10.09+1√(0.05)2+(0.12)2)
Calculating √(0.05)2+(0.12)2:
√0.0025+0.0144=√0.0169=0.13m
Now substituting back:
VC2=9×109⋅10−6⋅(10.09+10.13)
Calculating 10.09≈11.11 and 10.13≈7.69:
VC2=9×109⋅10−6⋅(11.11+7.69)=9×109⋅10−6⋅18.8
VC2=9×18.8≈169.2V
Step 4: Calculate the Potential Difference
The potential difference ΔV between the centers of the loops is:
ΔV=VC1−VC2=240V−169.2V≈70.8V
Final Answer
The potential difference between the centers of the loops is approximately 70.8V.
---
We have two circular loops with radii r1=0.05m and r2=0.09m. The distance between their centers is x=0.12m. Each loop has a uniform charge of Q=10−6C. We need to find the potential difference between the centers of the two loops.
The potential VC1 at the center of the first loop (with radius r1) due to its own charge is given by:
VC1=k⋅Q⋅⎛⎜
⎜⎝1r1+1√r22+x2⎞⎟
⎟⎠
Where k=9×109N⋅m2/C2.
- r1=0.05m
- r2=0.09m
- x=0.12m
VC1=9×109⋅10−6⋅(10.05+1√(0.09)2+(0.12)2)
√0.0081+0.0144=√0.0225=0.15m
VC1=9×109⋅10−6⋅(10.05+10.15)
Calculating 10.05=20 and 10.15≈6.67:
VC1=9×109⋅10−6⋅(20+6.67)=9×109⋅10−6⋅26.67
VC1=9×26.67≈240V
Similarly, the potential VC2 at the center of the second loop (with radius r2) is given by:
VC2=k⋅Q⋅⎛⎜
⎜⎝1r2+1√r21+x2⎞⎟
⎟⎠
VC2=9×109⋅10−6⋅(10.09+1√(0.05)2+(0.12)2)
√0.0025+0.0144=√0.0169=0.13m
VC2=9×109⋅10−6⋅(10.09+10.13)
Calculating 10.09≈11.11 and 10.13≈7.69:
VC2=9×109⋅10−6⋅(11.11+7.69)=9×109⋅10−6⋅18.8
VC2=9×18.8≈169.2V
The potential difference ΔV between the centers of the loops is:
ΔV=VC1−VC2=240V−169.2V≈70.8V
The potential difference between the centers of the loops is approximately 70.8V.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
Two rings of radii 5m and 10m move in opposite directions with velocity 20 m/s and 10 m/s respectively, on a conducting curface S. There is a uniform magnetic field of magnitude 0.1T perpendicular to the plane of the rings. Find the potential difference between the highest points of the two rings.
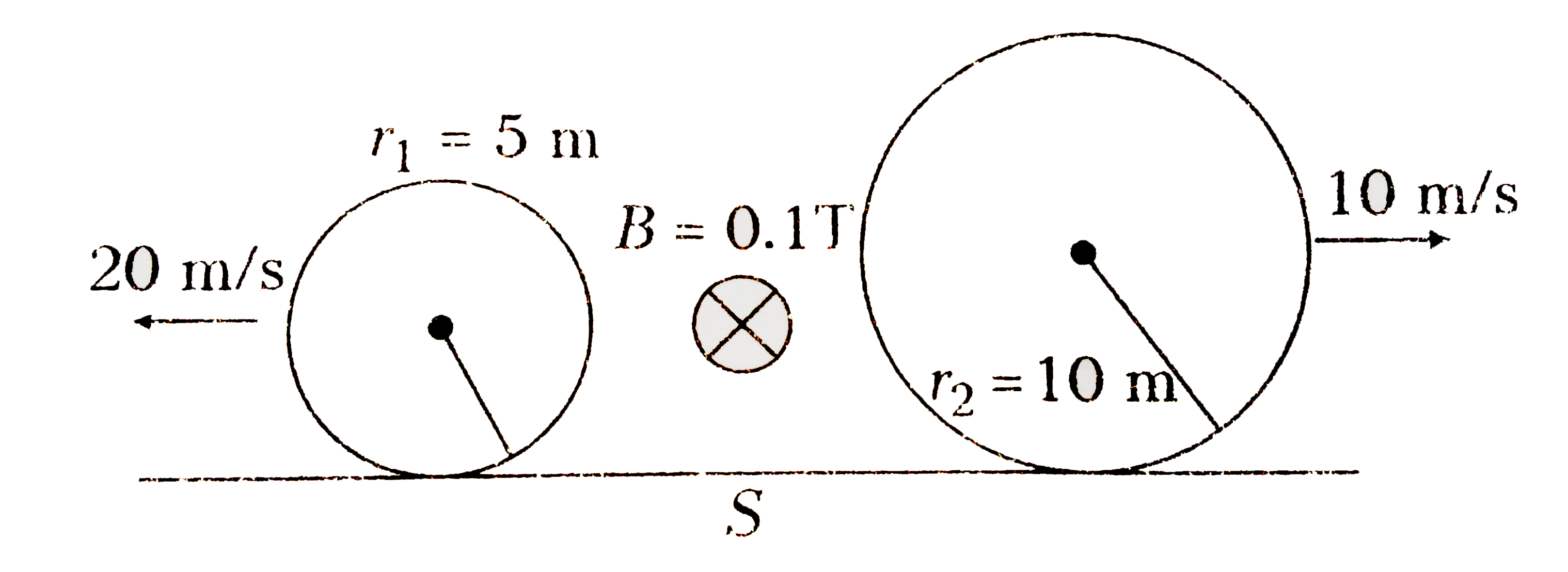
View SolutionTwo thin wire rings each having radius R are placed at distance d apart with their axes coinciding. The charges on the two are +Q and −Q. The potential difference between the centre so the two rings is
View SolutionA chrage of 5C is given a displacement of 0.5m. The work done in the process is 10J. The potetnial difference between the two points will be
View SolutionThe force between two charges 0.06m apart is 5N. If each charge is moved towards the other by 0.01 m, then the force between them will become
View SolutionRadii of two conducting circular loops are b and a respectively, where b>>a Centres of both loops coincide but planes of both loops are perpendicular each other. The value of mutual inductance for these loops
View SolutionThe plane of a rectangular loop of wire with sides 0.05 m and 0.08 m is parallel to a uniform magnetic field of induction 1.5×10−2T. A current of 10.0 ampere flows through the loop. If the side of length 0.08 m is normal and the side of length 0.05 m is parallel to the lines of induction, then the torque acting on the loop is
View SolutionA circular loop of radius r moves with a constant velocity v in a region with uniform magnetic field B. Calculate the potential difference between two points (A,B), (C,D), and (E,F) located on the loop.

View SolutionTwo metal spheres of radii 0.01 m and 0.02 m are given a charge of 15 mC and 45 mC, respectively. They are then connected by a wire. The final charge on the first is …×10−3C.
View SolutionA circular loop of area 0.01m2 carrying a current of 10A, is held perpendicular to a magnetic field of intensity 0.1T. The torque acting on the loop is
View SolutionB0 is the magnetic field at point P fir s given straight wire as shown in figure. If this wire is bent into a circular loop,then magnetic field at the center of the loop is
_PHY_E06_051_Q01.png)
View Solution
