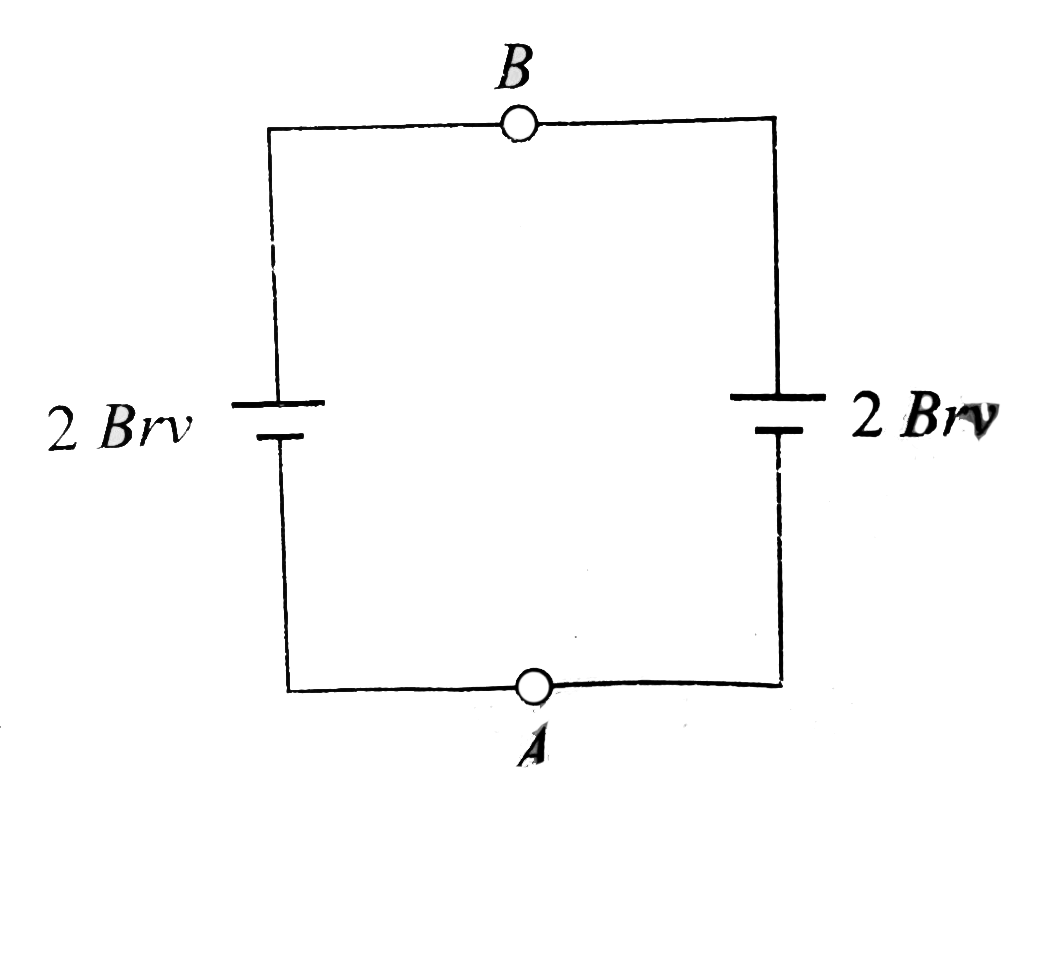
A circular loop of radius r moves with a constant velocity v in a region with uniform magnetic field B. Calculate the potential difference between two points (A,B), (C,D), and (E,F) located on the loop.

This illustration highlights a very common misconception in students. We know that when a closed loop translates in a uniform magnetic field, the net emf induced in the loop is zero. Students jump to the conclusion that the potential difference acroos any two points on the loop should also be zero. This are on a diameter that is oriented perpendicular to the direction of motion of the loop. Since net induced emf is zero there will be no induced currents in the loop. we can, therefore, cut the loop along the diameter AB and divided it into two semicircular loop without affectiving the physics of the problem. Each of these loop can in turn be replaced by straight conductors of length 2r. The induced emf across each of these conductors is B(2r)v and the potential difference across AB is B(2r)v. Note that when we travel through the whole circuit, the net induced emf is still zero as the two emf s cancel each other. In a similar manner, we can show that the potential difference between E and F is 2Brvsinθ where θ is the angle between line EF and the difference between C and D will be zero because θ=0∘ for this case.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Solved Example
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A conducting rod is moved with a constant velocity v in a magnetic field. A potential difference appears across the two ends
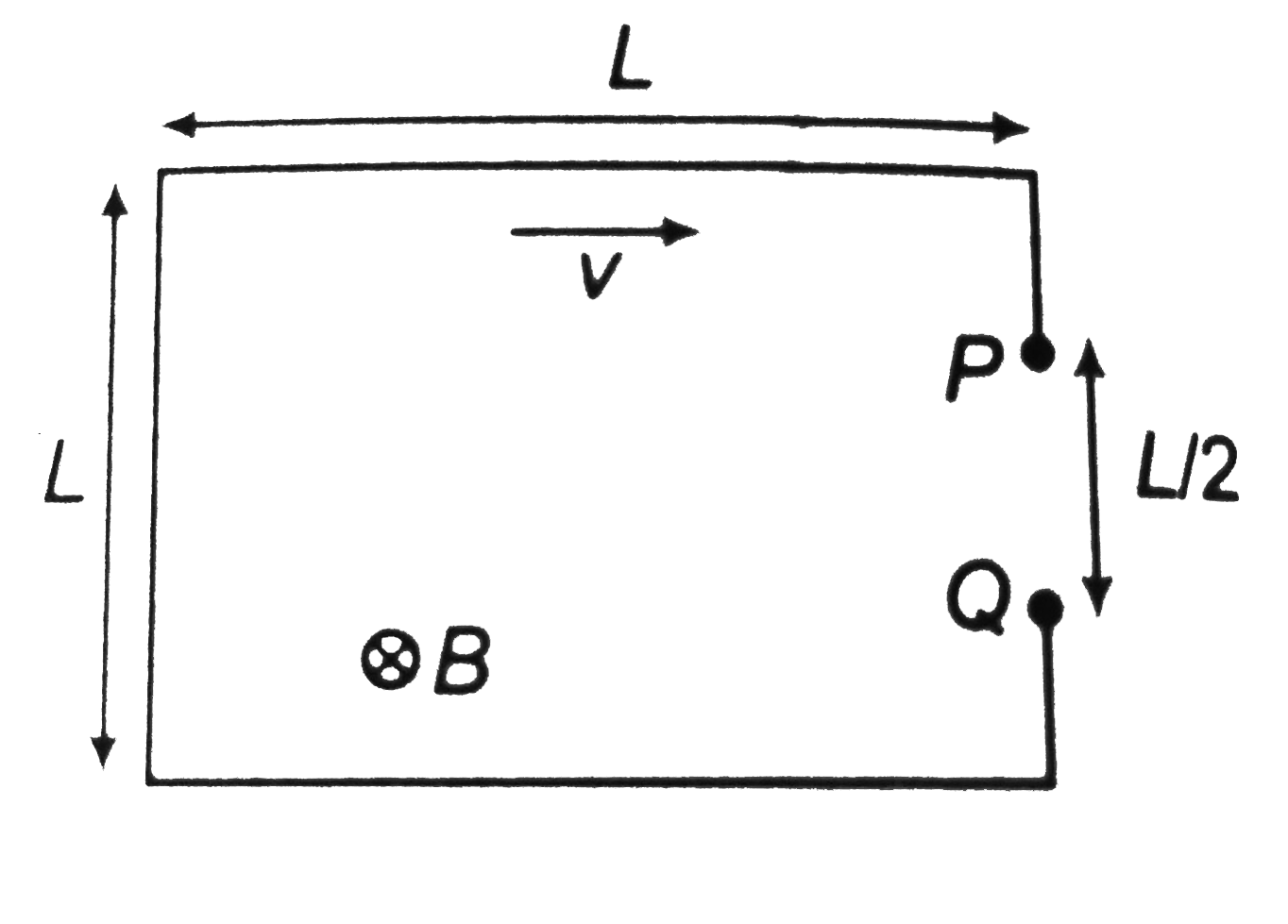
View SolutionThe loop shown moves with a velocity v in a uniform magnetic field of magnitude B, directed into the paper. The potential differene between point P and Q is e. Then
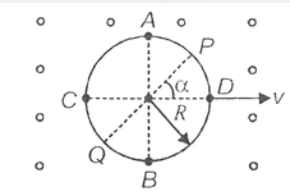
View SolutionA conducting ring of radius R is being moved in a region of uniform magnetic field as shown. Let EAB represent the potential difference between A and B then
View SolutionA ring of radius R moves with a velocity v in a uniform static magnetic field B as shown in diagram. The emf between P and Q is
View SolutionIn the figure shown a T−shaped conductor moves with constant angular velocity ω in a plane perpendicular to uniform magnetic field B. The potential difference VA−VB is

View SolutionIn figure two points A and B are located in a region of electric field . The potential difference VB−VA is
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA semicircular loop of radius R is rotated with an angular velocity ω perpendicular to the plane of a magnetic field B as shown in the figure. Emf Induced in the loop is

View SolutionThe loop shown moves with a velocity v in a uniform magnetic field of magnitude B, directed into the paper. The potential differene between point P and Q is e. Then

A e=12BLv
B e=BLv
C P is positive with respect to Q
D Q is positive with respect to P
View SolutionA uniform circular loop of radius a and resistance R is pulled at a constant velocity v out of a region of a uniform plane of the loop and the velocity are both perpendicular to B. Then the electrical power in the circular loop at the instant when the arc (of the circular loop) outside the region of magnetic field subtends an angle π3 at the centre of the loop is
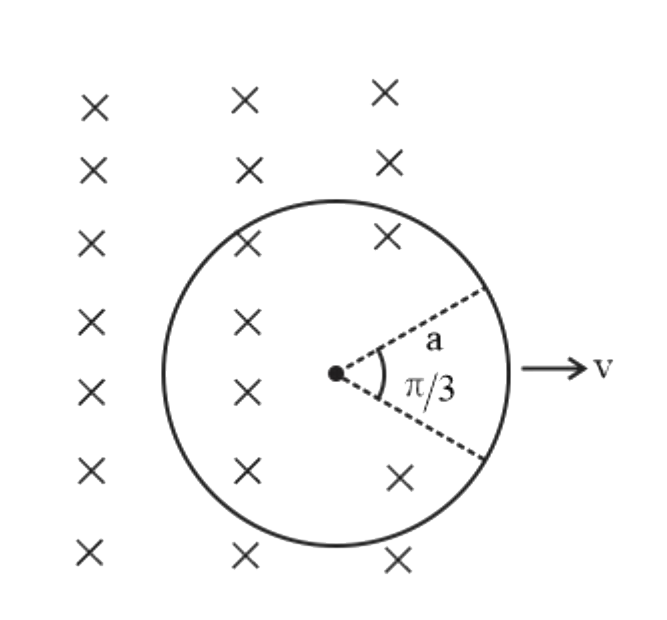
View Solution
