Figure shows a path followed by a particle and position of a particle at any instant. Four different students have represented the velocity vectors and acceleration vectors at the given instant. Which vector diagram cannot be true in any situation? (In each figure, velocity is tangential to the trajectory).

The correct Answer is:D
→anet in curved path is always within the curvature of trajectory.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
Figure shows path followed by a particle and position of a particle at any instant. Four different students have represented the velocity vectors and acceleration vectors at the given instant. Which vector diagram can not be true in any situation? (In each figure velocity is tangential to the trajectory).
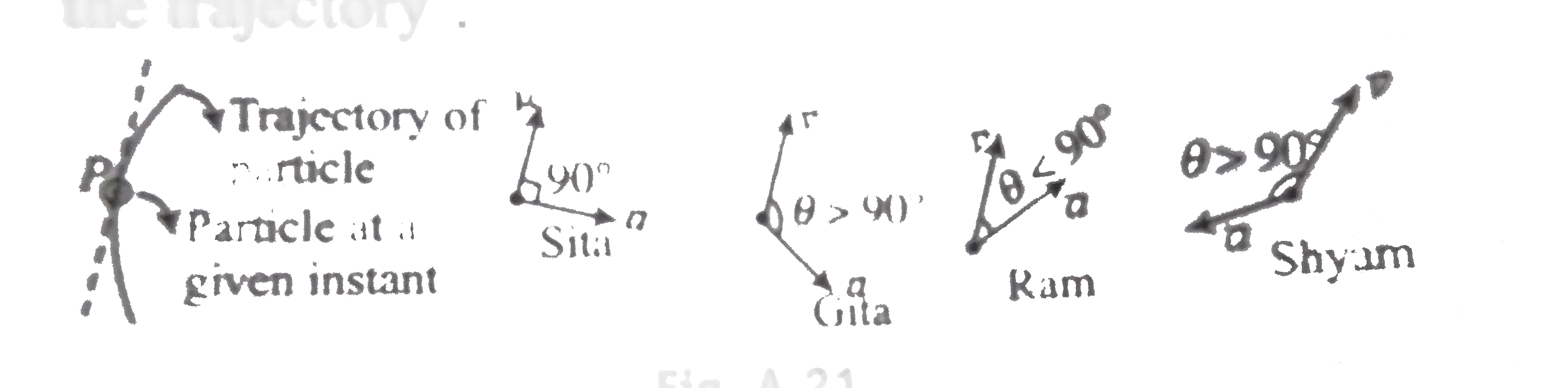
View SolutionThe position of a particle at any point instant is x . Find the velocity and acceleration at any instant .
View SolutionA particle starts traveling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track, is
View SolutionA particle starts travelling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track. Is
View SolutionFor a particle executing SHM, x = displacement from mean position, v = velocity and a = acceleration at any instant, then
View SolutionTwo particles A and B are projected from the same point in different direction in such a manner that their velocity vectors are shown in the diagram :−
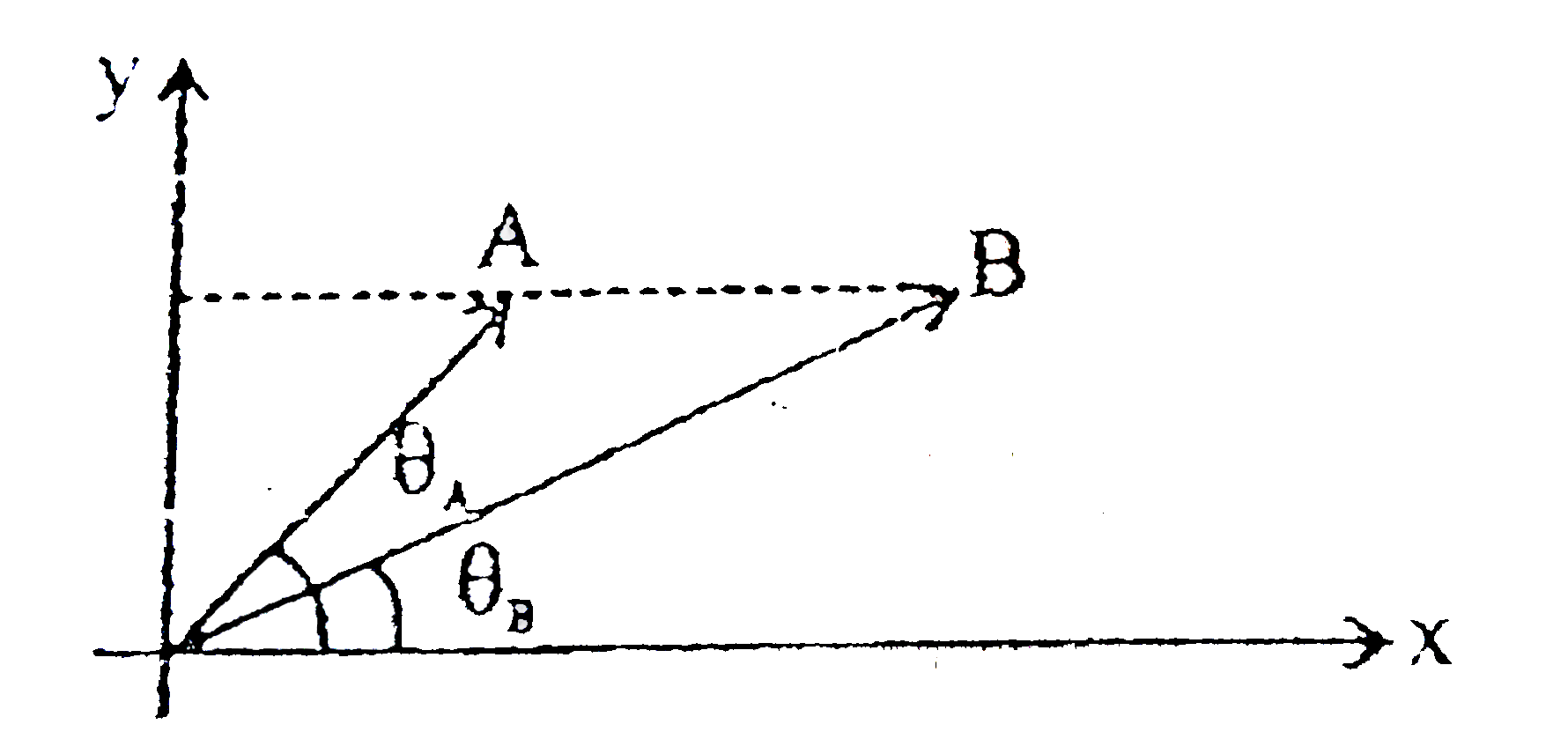 .
.
View SolutionThe position vector of a aprticle is given as →r=(t2−4t+6)ˆi+(t2)ˆj. The time after which the velocity vector and acceleration vector becomes perpendicular to each other is equal to
View SolutionThe position vector of a aprticle is given as →r=(t2−4t+6)ˆi+(t2)ˆj. The time after which the velocity vector and acceleration vector becomes perpendicular to each other is equal to
View SolutionPosition of a particle at any instant is given by x=3t2+1 , where x is in m and t in sec. Its average velocity in the time interval t=2 sec to t=3 sec will be :
View SolutionShow here are the velocity and acceleration vectors for an object in several different types of motion. In which case is the object slowing down and turning to the left ?
View Solution
