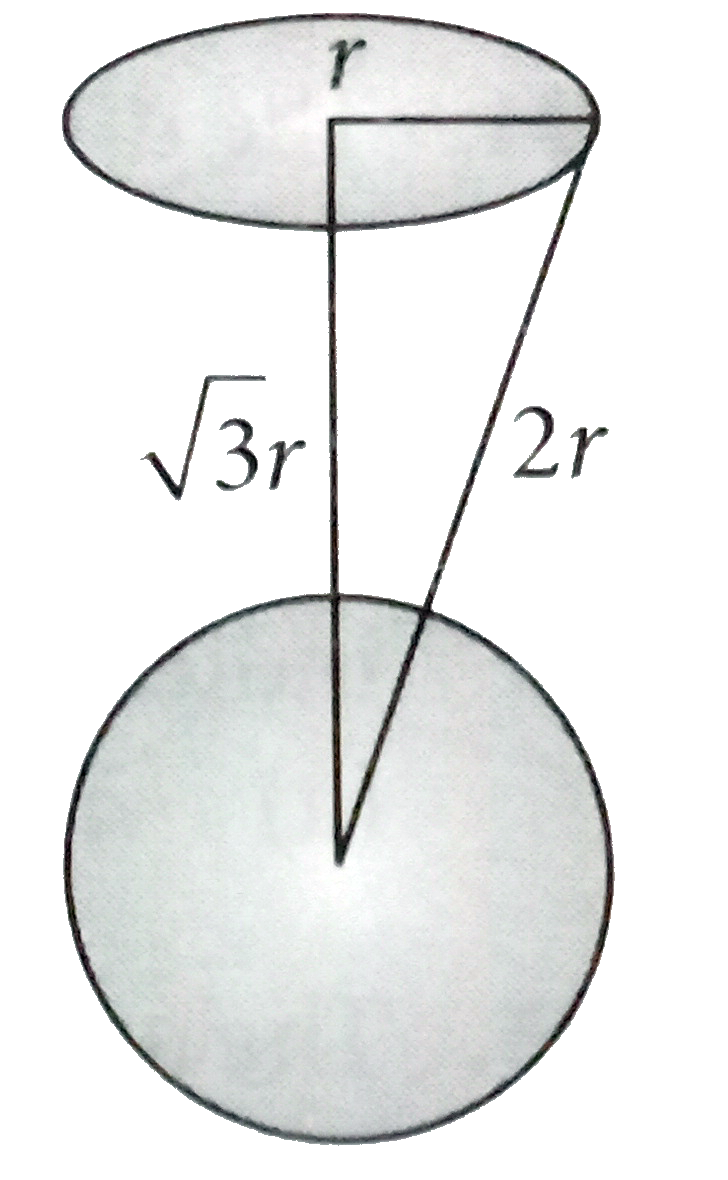
A uniform ring of mass m and radius r is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is directly above the centre of the sphere at a distance r√3 as shown in the figure. The gravitational force exerted by the sphere on the ring will be
GMm8r2
GMm4r2
√3GMm8r2
GMm8r3√3
The correct Answer is:C
dF=GMdm4r2
F=ΣdFcosθ
=ΣGMdm4r2cosθ
=GM4r2×√3r2rΣdm
=√3GMm8r2 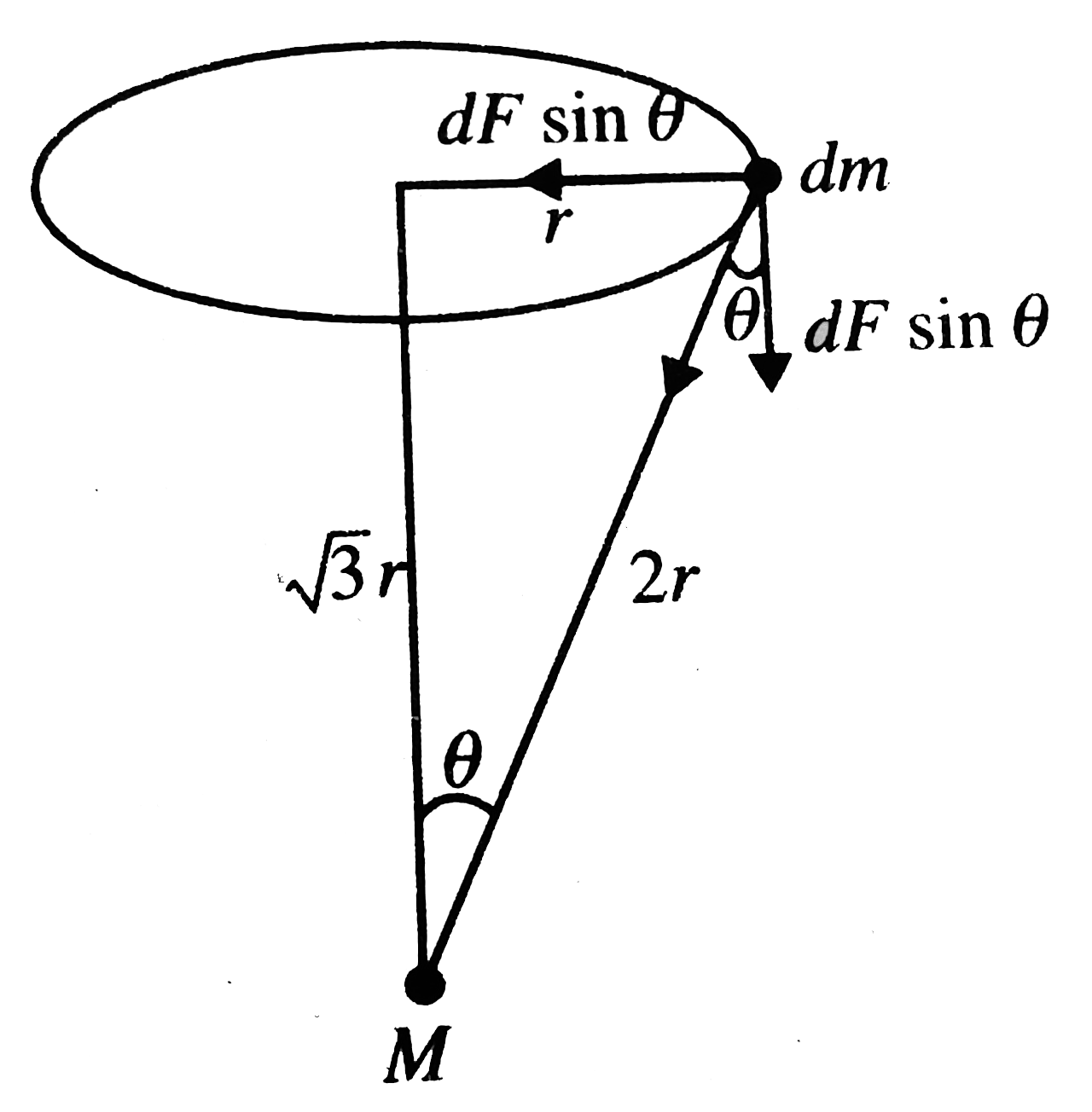
Alternative solution:
The gravitational field due to the ring at a distance √3r is given by
E=Gm(√3r)[r2+(√3r)2]32 or E=√3Gm8r2
The required force is EM i.e., (√3Gm)M/(8r2)
Topper's Solved these Questions
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:Multiple Correct
Explore 24 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:Assertion- Reasoning
Explore 13 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:Subjective
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
Similar Questions
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance √3a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View Solution
Knowledge Check
A uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at distance √3a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
AGMm8r2BGMm4r2C√3GMm8r2DGMm8r3√3
For a uniform ring of mass M and radius R at its centre
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionA uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and redius 4a. The centre of the shell falls on the surface of the iner sphere
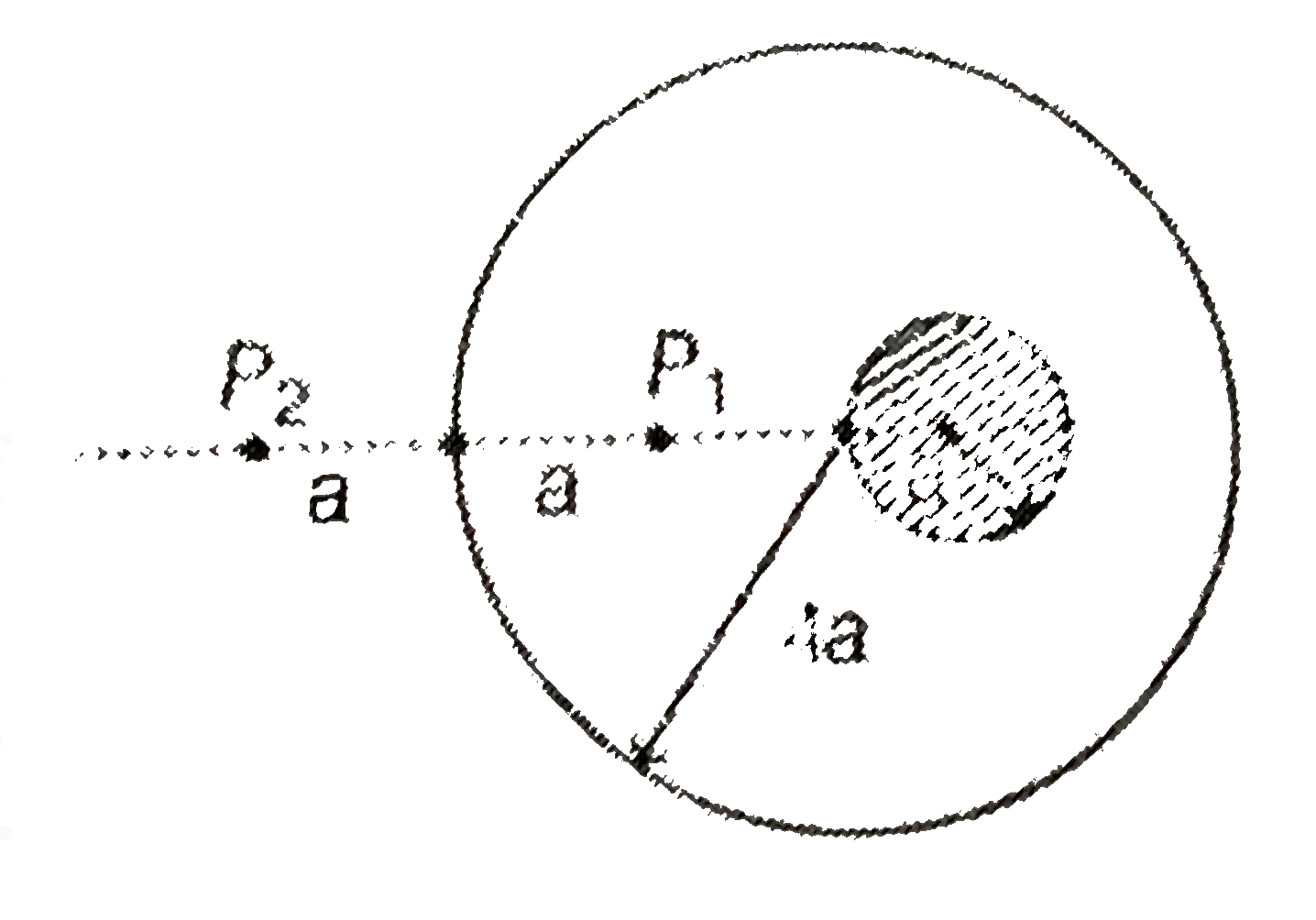
View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
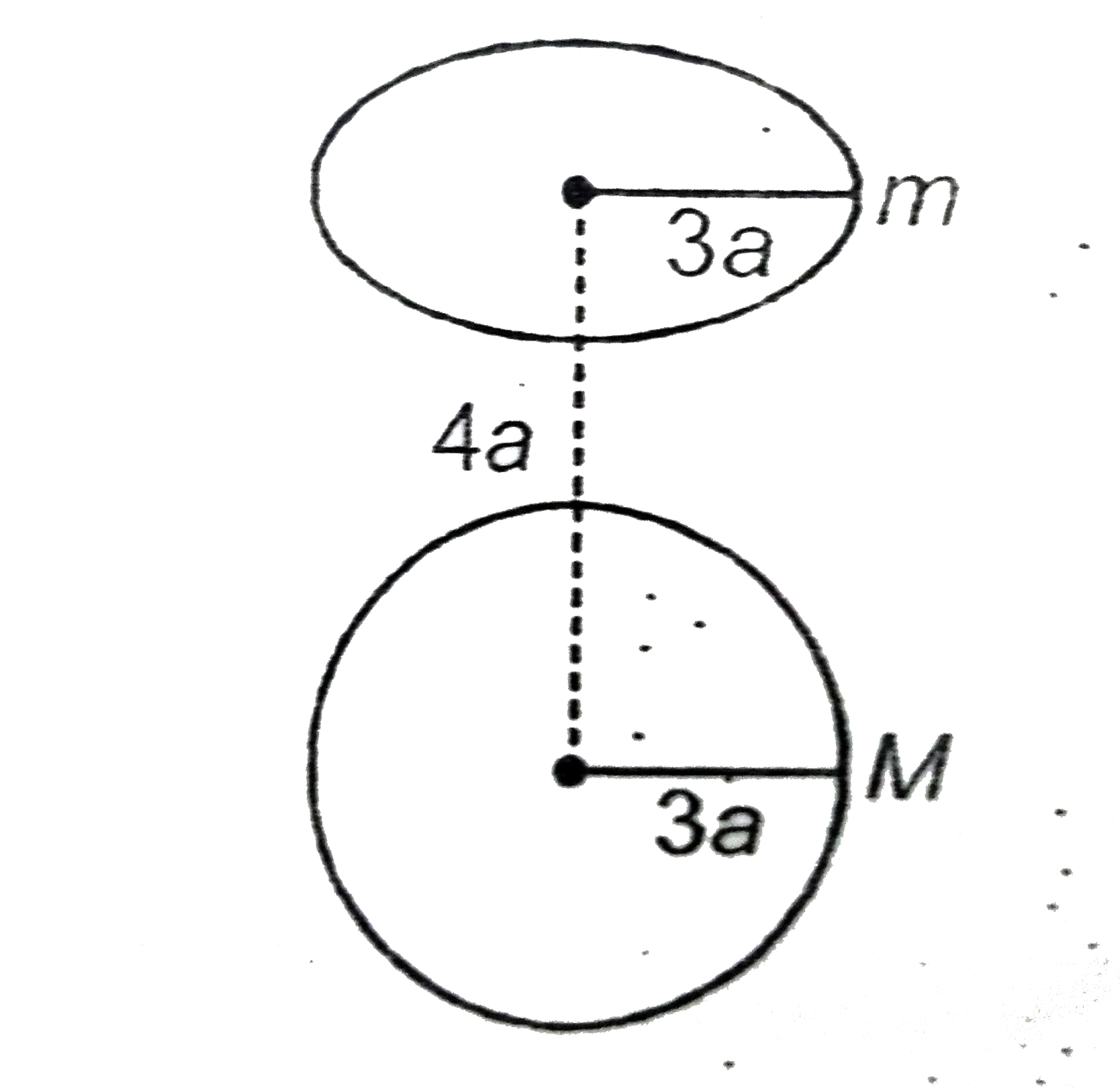
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionA uniform sphere of mass M and radius R is surrounded by a concentric spherical shell of same mass but radius 2R. A point mass is kept at a distance x(>R) in the region bounded by spheres as shown in the figure . The net gravitational force on the particle is

View Solution

