A body starts from rest from a point distant r0 from the centre of the earth. It reaches the surface of the earth whose radius is R. The velocity acquired by the body is
2GM√1R−1r0
√2GM(1R−1r0)
GM√1R−1r0
√GM(1R−1R0)
The correct Answer is:B
To solve the problem of finding the velocity acquired by a body starting from rest at a distance r0 from the center of the Earth and reaching the surface of the Earth (radius R), we can use the principle of conservation of mechanical energy. Here’s a step-by-step solution:
Step 1: Understand the Energy Conservation Principle
The total mechanical energy (potential energy + kinetic energy) of the system remains constant if only conservative forces (like gravity) are acting on it.
Step 2: Write the Initial and Final Energy Expressions
1. Initial Energy (at distance r0):
- Gravitational Potential Energy (U_i):
Ui=−GMmr0
- Kinetic Energy (K_i):
Ki=0(since it starts from rest)
- Total Initial Energy (E_i):
Ei=Ui+Ki=−GMmr0+0=−GMmr0
2. Final Energy (at the surface of the Earth):
- Gravitational Potential Energy (U_f):
Uf=−GMmR
- Kinetic Energy (K_f):
Kf=12mv2
- Total Final Energy (E_f):
Ef=Uf+Kf=−GMmR+12mv2
Step 3: Set Initial Energy Equal to Final Energy
Using the conservation of energy:
Ei=Ef
−GMmr0=−GMmR+12mv2
Step 4: Simplify the Equation
1. Cancel m from both sides (assuming m≠0):
−GMr0=−GMR+12v2
2. Rearranging gives:
12v2=GMR−GMr0
3. Factor out GM:
12v2=GM(1R−1r0)
Step 5: Solve for v2
Multiply both sides by 2:
v2=2GM(1R−1r0)
Step 6: Take the Square Root to Find v
v=√2GM(1R−1r0)
Final Answer
The velocity acquired by the body when it reaches the surface of the Earth is:
v=√2GM(1R−1r0)
The total mechanical energy (potential energy + kinetic energy) of the system remains constant if only conservative forces (like gravity) are acting on it.
1. Initial Energy (at distance r0):
- Gravitational Potential Energy (U_i):
Ui=−GMmr0
- Kinetic Energy (K_i):
Ki=0(since it starts from rest)
- Total Initial Energy (E_i):
Ei=Ui+Ki=−GMmr0+0=−GMmr0
- Gravitational Potential Energy (U_f):
Uf=−GMmR
- Kinetic Energy (K_f):
Kf=12mv2
- Total Final Energy (E_f):
Ef=Uf+Kf=−GMmR+12mv2
Using the conservation of energy:
Ei=Ef
−GMmr0=−GMmR+12mv2
1. Cancel m from both sides (assuming m≠0):
−GMr0=−GMR+12v2
2. Rearranging gives:
12v2=GMR−GMr0
3. Factor out GM:
12v2=GM(1R−1r0)
Multiply both sides by 2:
v2=2GM(1R−1r0)
v=√2GM(1R−1r0)
The velocity acquired by the body when it reaches the surface of the Earth is:
v=√2GM(1R−1r0)
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
A body is released from a point of distance R' from the centre of earth. Its velocity at the time of striking the earth will be (R’>Re)
View SolutionA body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is
View Solution
Knowledge Check
The escape velocity from the surface of the earth is (where RE is the radius of the earth )
A√2gREB√gREC2√gRED√3gRE
The escape velocity of a body from the surface of the earth is equal to
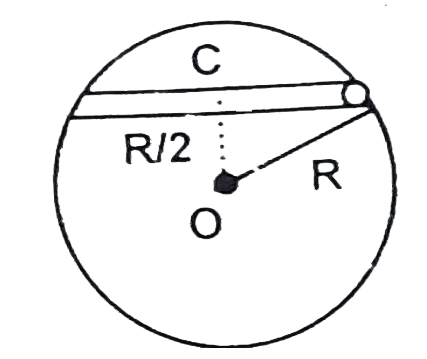
View SolutionA tunnel is dug across the earth of mass 'M' and radius 'R' at a distance R/2 from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is
View SolutionA body projected from the surface of the earth attains a height equal to the radius of the earth. The velocity with which the body was projected is
View SolutionAn asteroid of mass m(m<<mE) is approaching with a velocity 12 km/s when it is at distance of 10 R from the centre of earth (where R is radius of earth). When it reaches at the surface of Earth, its velocity is (Nearest Integer) in km/s
View SolutionThe distance of geostationary satellite from the centre of the earth (radius R) is nearest to
View SolutionGravitational potential at a height R from the surface of the earth will be [Take M = mass of the earth, R = radius of the earth]
View SolutionA man weighs 'W' on the surface of the earth and his weight at a height 'R' from surface of the earth is (R is Radius of the earth )
View Solution
