Two masses m1 and m2 at an infinite distance from each other are initially at rest, start interacting gravitationally. Find their velocity of approach when they are at a distance r apart.
Since they move under mutual attraction and no external force acts on them, their momentum and energy are conserved. Therefore,
∴0=12M1v21+12M2v22−GM1M2s
It is zero because in the beginning, both kinetic energy and potential energy are zero.
0=M1v1+M2v2
Solving the equations
v21=2GM22s(M1+M2)
and v22=2GM21s(M1+M2)
V (velocity of approach) =v1−(−v2)=v1+v2
=√2G(M1+M2)s
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.1
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.2
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Two particles of masses m1andm2 are intially at rest at an infinite distance apart. If they approach each other under their mutual interaction given by F=−Kr2. Their speed of approach at the instant when they are at a distance d apart is
View Solution10 Two particles of masses m1 and m2 initially at rest start moving towards each other under their mutual force of attraction. The speed of the centre of mass at any time t, when they are at a distance r apart, is
View SolutionTwo masses m1andm2 are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
View SolutionTwo particles of mass m and M are initialljy at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when d is their separation at any instant
View SolutionTwo particles of masses m and M are initially at rest at an infinite distance apart. They move towards each other and gain speeds due to gravitational attraction. Find their speeds when the separation between the masses becomes equal to d.
View SolutionBinary stars of comparable masses m1 and m2 rotate under the influence of each other's gravity with a time period T. If they are stopped suddenly in their motions, find their relative velocity when they collide with each constant of gravitation.
View SolutionTwo bodies of mass m1andm2 are initially at rest placed infinite distance apart. They are then allowed to move towards each other under mutual gravitational attraction. Show that their relative velocity of approach at separation r between them is:
View SolutionTwo points mass m and 2m are kept at a distance a. Find the speed of particles and their relative velocity of approach when separation becomes a/2.
View SolutionFind the force of interaction of two dipoles , if the two dipole moments are parallel to each other and placed at a distance x apart
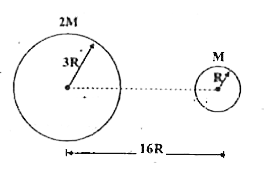
View SolutionTwo spherical bodies of masses 2M and M and radii 3R and R respectively are held at a distance 16R from each other in free space. When they are released they start approaching each other due to the gravitational force of attraction , then find
(a) the ratio of their accelerations during their motion
(b) their velocitites at the time of impact.
View Solution
