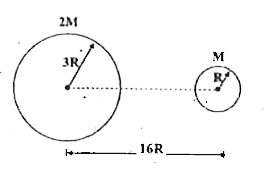
Two spherical bodies of masses $2 M$ and $M$ and radii $3 R$ and $R$ respectively are held at a distance $16 R$ from each other in free space. When they are released they start approaching each other due to the gravitational force of attraction , then find
$(a)$ the ratio of their accelerations during their motion
$(b)$ their velocitites at the time of impact.

Video Solution

Text Solution

Verified by Experts

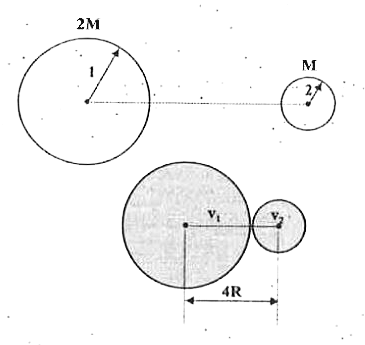
Taking both the bodies as a system, from conserving momentum of the system
$m_{1} v_{1} - m_{2} v_{2} = 0 \Rightarrow \frac{m_{1}}{m_{2}} = \frac{v_{2}}{v_{1}} = 2$
again , if the accelerations are $a_{1}$ and $a_{2}$ , the net external force on the system $= 0$
$\Rightarrow {\vec{a}}_{C M} = 0 \Rightarrow m_{1} a_{1} - m_{2} a_{2} = 0$
$\frac{m_{1}}{m_{2}} = \frac{a_{2}}{a_{1}} = 2$
Now conserving the total mechanical energy, we have
$- \frac{G (2 M) M}{16 R} = - \frac{G (2 M) M}{4 R} + \frac{1}{2} (2 M) v_{1}^{2} + \frac{1}{2} (M) v_{2}^{2}$
$v_{1} = \sqrt{\frac{G M}{8 R}}$ , $v_{2} = 2 \sqrt{\frac{G M}{8 R}}$
Note : The velocities and accelerations are w.r.t. the inertial reference frame (i.e. the centre of mass of the system).

Updated on:21/07/2023