Two spherical bodies of masses m and 5m and radii R and 2R respectively, are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, the distance covered by smaller sphere just before collision is
2.5 R
4.5 R
7.5 R
1.5 R
The correct Answer is:C
To solve the problem, we need to find the distance covered by the smaller sphere (mass m) just before it collides with the larger sphere (mass 5m).
1. Identify the Initial Conditions:
- Mass of the smaller sphere, m
- Mass of the larger sphere, 5m
- Radius of the smaller sphere, R
- Radius of the larger sphere, 2R
- Initial separation between their centers, 12R
2. Determine the Distance Between Their Surfaces:
- The distance between the surfaces of the spheres is given by:
Distance between surfaces=Distance between centers−(Radius of smaller sphere+Radius of larger sphere)
- Thus,
Distance between surfaces=12R−(R+2R)=12R−3R=9R
3. Use the Center of Mass Concept:
- The center of mass (COM) of the system does not move since there are no external forces acting on it. The position of the center of mass can be calculated as:
xCOM=m⋅x+5m⋅(9R−x)m+5m
- Here, x is the distance covered by the smaller sphere before collision.
4. Set Up the Center of Mass Equation:
- Since the center of mass remains stationary, we can set the equation for the center of mass to equal its initial position:
m⋅x+5m⋅(9R−x)=0
- Simplifying this gives:
x+5(9R−x)=0
- This simplifies to:
x+45R−5x=0
- Rearranging gives:
4x=45R⟹x=45R4=11.25R
5. Calculate the Distance Covered by the Smaller Sphere:
- The distance covered by the smaller sphere just before collision is x:
x=7.5R
Final Answer:
The distance covered by the smaller sphere just before collision is 7.5R.
- Mass of the smaller sphere, m
- Mass of the larger sphere, 5m
- Radius of the smaller sphere, R
- Radius of the larger sphere, 2R
- Initial separation between their centers, 12R
- The distance between the surfaces of the spheres is given by:
Distance between surfaces=Distance between centers−(Radius of smaller sphere+Radius of larger sphere)
- Thus,
Distance between surfaces=12R−(R+2R)=12R−3R=9R
- The center of mass (COM) of the system does not move since there are no external forces acting on it. The position of the center of mass can be calculated as:
xCOM=m⋅x+5m⋅(9R−x)m+5m
- Here, x is the distance covered by the smaller sphere before collision.
- Since the center of mass remains stationary, we can set the equation for the center of mass to equal its initial position:
m⋅x+5m⋅(9R−x)=0
- Simplifying this gives:
x+5(9R−x)=0
- This simplifies to:
x+45R−5x=0
- Rearranging gives:
4x=45R⟹x=45R4=11.25R
- The distance covered by the smaller sphere just before collision is x:
x=7.5R
The distance covered by the smaller sphere just before collision is 7.5R.
Topper's Solved these Questions
Similar Questions
Two spherical bodies of masses m and 6m and radii R and 2R respectively are released in free space with initial separation between their centres equal to 10 R . If they attract each other due to gravitational force only , then the distance covered by smaller sphere just before collisions will be
View SolutionTwo spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is
View Solution
Knowledge Check
Two spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
A−GMrB−2GMrC−GM2rD−4GMr
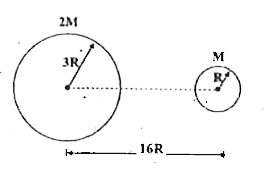
Two spherical bodies of masses 2M and M and radii 3R and R respectively are held at a distance 16R from each other in free space. When they are released they start approaching each other due to the gravitational force of attraction , then find
(a) the ratio of their accelerations during their motion
(b) their velocitites at the time of impact.
View SolutionTwo concentric shells have masses M and m and their radii are R and r, respectively, where R>r. What is the gravitational potential at their common centre?
View SolutionTwo homogeneous spheres A and B of masses m and 2m having radii 2a and a respectively are placed in touch . The distance of the centre of mass from the first sphere is
View SolutionTwo concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is

View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View SolutionTwo spherical bodies of mass m1 & m2 are having radius 1 m & 2 m respectively. The gravitational field of the two bodies with their radial distance is shown below. The value of m1m2 is
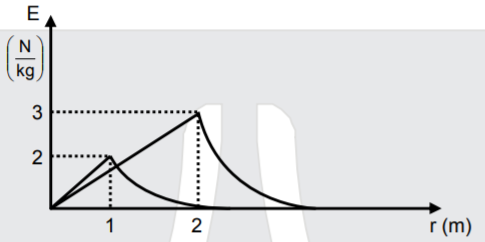 -
-
View SolutionTwo objects of masses m and 4m are at rest at an infinite separation. They move towards each other under mutual gravitational attraction. If G is the universal gravitaitonal constant, then at separation r
View Solution

