Two vertical rods of equal lengths, one of steel and the other of copper, are suspended from the ceiling at a distance l apart and are connected rigidly to a rigid horizontal bar at their lower ends. If AS and AC be their respective cross-sectional areas, and YS and YC,their respective Young's moduli of elasticities, where should a vertical force F be applied to the horizontal bar in order that the bar remains horizontal?
To solve the problem, we need to determine where to apply a vertical force F on a horizontal bar connected to two vertical rods made of steel and copper, such that the bar remains horizontal. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have two vertical rods (one steel and one copper) of equal lengths suspended from the ceiling. They are connected at their lower ends to a rigid horizontal bar. The rods are at a distance l apart.
Step 2: Define Variables
Let:
- AS = Cross-sectional area of the steel rod
- AC = Cross-sectional area of the copper rod
- YS = Young's modulus of steel
- YC = Young's modulus of copper
- FS = Force in the steel rod
- FC = Force in the copper rod
- F = Applied vertical force on the horizontal bar
- x = Distance from the steel rod to the point where force F is applied
Step 3: Apply Equilibrium Conditions
Since the horizontal bar remains horizontal, the sum of the forces in the vertical direction must equal zero:
FS+FC=F
Step 4: Relate Forces to Young's Modulus
The extension produced in both rods must be the same for the bar to remain horizontal. Therefore, we can use the relationship:
FSASYS=FCACYC
From this, we can express FS in terms of FC:
FS=FCASYSACYC
Step 5: Substitute into the Force Equation
Substituting FS into the equilibrium equation:
FCASYSACYC+FC=F
Factoring out FC:
FC(ASYSACYC+1)=F
Thus, we can solve for FC:
FC=FASYSACYC+1
Step 6: Find FS
Now substituting FC back to find FS:
FS=F⋅ASYSACYC(ASYSACYC+1)
Step 7: Take Moments About the Steel Rod
Taking moments about the steel rod:
FC⋅l=F⋅x
Substituting FC:
FASYSACYC+1⋅l=F⋅x
Cancelling F from both sides (assuming F≠0):
lASYSACYC+1=x
Step 8: Solve for x
Rearranging gives us:
x=l1+ASYSACYC=lACYCACYC+ASYS
Final Answer
Thus, the distance x from the steel rod where the force F should be applied is:
x=lACYCACYC+ASYS
We have two vertical rods (one steel and one copper) of equal lengths suspended from the ceiling. They are connected at their lower ends to a rigid horizontal bar. The rods are at a distance l apart.
Let:
- AS = Cross-sectional area of the steel rod
- AC = Cross-sectional area of the copper rod
- YS = Young's modulus of steel
- YC = Young's modulus of copper
- FS = Force in the steel rod
- FC = Force in the copper rod
- F = Applied vertical force on the horizontal bar
- x = Distance from the steel rod to the point where force F is applied
Since the horizontal bar remains horizontal, the sum of the forces in the vertical direction must equal zero:
FS+FC=F
The extension produced in both rods must be the same for the bar to remain horizontal. Therefore, we can use the relationship:
FSASYS=FCACYC
From this, we can express FS in terms of FC:
FS=FCASYSACYC
Substituting FS into the equilibrium equation:
FCASYSACYC+FC=F
Factoring out FC:
FC(ASYSACYC+1)=F
Thus, we can solve for FC:
FC=FASYSACYC+1
Now substituting FC back to find FS:
FS=F⋅ASYSACYC(ASYSACYC+1)
Taking moments about the steel rod:
FC⋅l=F⋅x
Substituting FC:
FASYSACYC+1⋅l=F⋅x
Cancelling F from both sides (assuming F≠0):
lASYSACYC+1=x
Rearranging gives us:
x=l1+ASYSACYC=lACYCACYC+ASYS
Thus, the distance x from the steel rod where the force F should be applied is:
x=lACYCACYC+ASYS
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Solved Examples
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A composite tube is made by striking a thin steel tube on a brass tube. If AS and AB are the respective sectional areas of the steel and brass tubes and YS and YB their Young's moduli, then find the Young's modulus of single tube of the same length and total sectional area, which would behave in the same fashion as that of the composite tube.
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
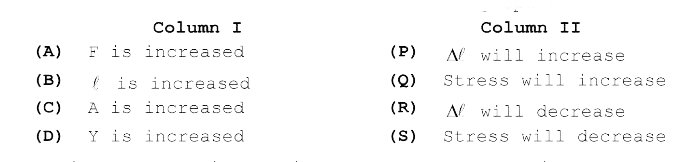
View Solution
Knowledge Check
Let Ys and YA represent Young's modulus for steel and aluminium respectively. It is said that steel is more elastic than aluminium.Therefore, it follows that
AYs=YABYs<YACYs>YADYSYA=0A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The differnece in the levels of the liquid in the two vertical tubes is h. then
 Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
Av22−v21=2ghBv22+v21=2ghCv22−v21=ghDv22+v21=gh
A copper rod length L and radius r is suspended from the ceiling by one of its ends. What will be elongation of the rod due to its own weight when p andYare the density and Young's modulus of the copper respectively?
View SolutionA smooth uniform, string of natural length l, cross-sectional area A and Young’s modulus Y is pulled along its length by a force F on a horizontal surface. Find the elastic potential energy stored in the string.
View SolutionA metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y,then the work done is proportional to
View SolutionA liquid flows through a horizontal tube. The velocities of the liquid in the two sections, which have areas of cross section A1 and A2 are v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h. Then

View SolutionA uniform bar of square cross-section is lying along a frictionless horizontal surface. A horizontal force is applied to pull it from one of its ends then

View SolutionA uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
View Solution
