A uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
To determine the elongation of a uniform rod of length L and mass M when pulled horizontally with a force F, we can follow these steps:
Step 1: Understand the Setup
We have a uniform rod of length L and mass M being pulled horizontally on a smooth surface with a force F. The rod is uniform, so its mass is evenly distributed along its length.
Step 2: Calculate the Acceleration
The acceleration a of the rod can be calculated using Newton's second law:
a=FM
Step 3: Consider an Element of the Rod
Let’s consider a small element of the rod of length dx located at a distance x from the free end. The force acting on this elemental section due to the applied force F can be expressed as:
F′=F⋅xL
This is because the force is distributed along the length of the rod.
Step 4: Calculate the Stress in the Element
The stress σ in the elemental section can be calculated using the formula:
σ=F′A=F⋅xLA
where A is the cross-sectional area of the rod.
Step 5: Calculate the Elongation of the Element
The elongation dδ of the differential element dx can be expressed using Young's modulus Y:
dδ=σ⋅dxY=F⋅xL⋅dxA⋅Y
Step 6: Integrate to Find Total Elongation
To find the total elongation δ of the rod, we need to integrate dδ from 0 to L:
δ=∫L0F⋅xL⋅dxA⋅Y
This simplifies to:
δ=FA⋅Y⋅L∫L0xdx
Calculating the integral:
∫L0xdx=L22
Thus, we have:
δ=FA⋅Y⋅L⋅L22=F⋅L2⋅A⋅Y
Final Result
The elongation of the rod when pulled by a force F is given by:
δ=F⋅L2⋅A⋅Y
We have a uniform rod of length L and mass M being pulled horizontally on a smooth surface with a force F. The rod is uniform, so its mass is evenly distributed along its length.
The acceleration a of the rod can be calculated using Newton's second law:
a=FM
Let’s consider a small element of the rod of length dx located at a distance x from the free end. The force acting on this elemental section due to the applied force F can be expressed as:
F′=F⋅xL
This is because the force is distributed along the length of the rod.
The stress σ in the elemental section can be calculated using the formula:
σ=F′A=F⋅xLA
where A is the cross-sectional area of the rod.
The elongation dδ of the differential element dx can be expressed using Young's modulus Y:
dδ=σ⋅dxY=F⋅xL⋅dxA⋅Y
To find the total elongation δ of the rod, we need to integrate dδ from 0 to L:
δ=∫L0F⋅xL⋅dxA⋅Y
This simplifies to:
δ=FA⋅Y⋅L∫L0xdx
Calculating the integral:
∫L0xdx=L22
Thus, we have:
δ=FA⋅Y⋅L⋅L22=F⋅L2⋅A⋅Y
The elongation of the rod when pulled by a force F is given by:
δ=F⋅L2⋅A⋅Y
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Solved Examples
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A uniform rod of length L and density ρ is being pulled along a smooth floor with a horizontal acceleration α (see Fig.) The magnitude of the stress at the transverse cross-section through the mid-point of the rod is……..
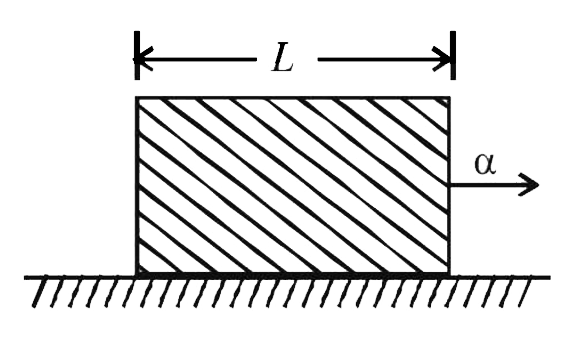
View SolutionA uniform rod of length L and density ρ is being pulled along a smooth floor with a horizontal acceleration α (see Fig.) The magnitude of the stress at the transverse cross-section through the mid-point of the rod is……..

View Solution
Knowledge Check
A wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAl
A 5kg rod of square cross section 5cm on a side and 1m long is pulled along a smooth horizontal surface by a force applied at one end. The rod has a constant acceleration of 2ms−12. Determine the elongation in the rod. (Young's modulus of the material of the rod is 5×103N/m9).
View SolutionA rod of uniform cross sectional area 5mm2 weighing5kg and length 1m is suspended vertically from a fixed support the elongation produced in the rod if [Young's modulus of material, Y=2x1011Nm2 and g=10ms−2]
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.

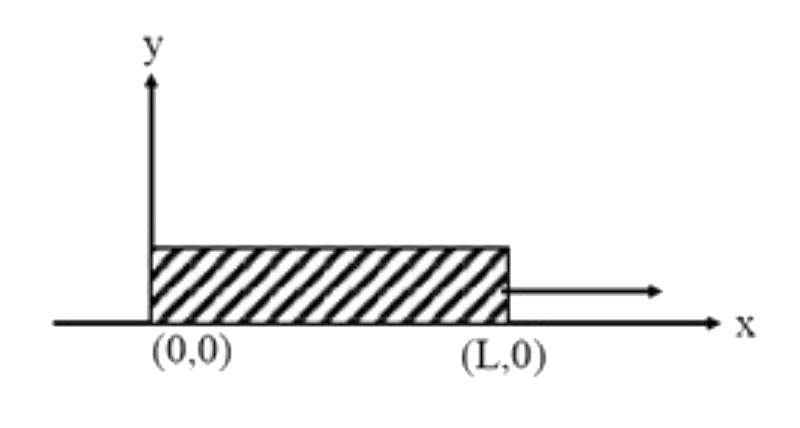
View SolutionA uniform rod of length L and mass M has been placed on a rough horizontal surface as shown in the figure. The rod is pulled by applying a horizontal force. The coefficient of friction μ between the surface and the rod is given by
μ={μ0x0≤x≤L0x>L, where μ0 is a positive constant. The heat generated due to friction as the rod moves by a distance L is
View SolutionA rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is

View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
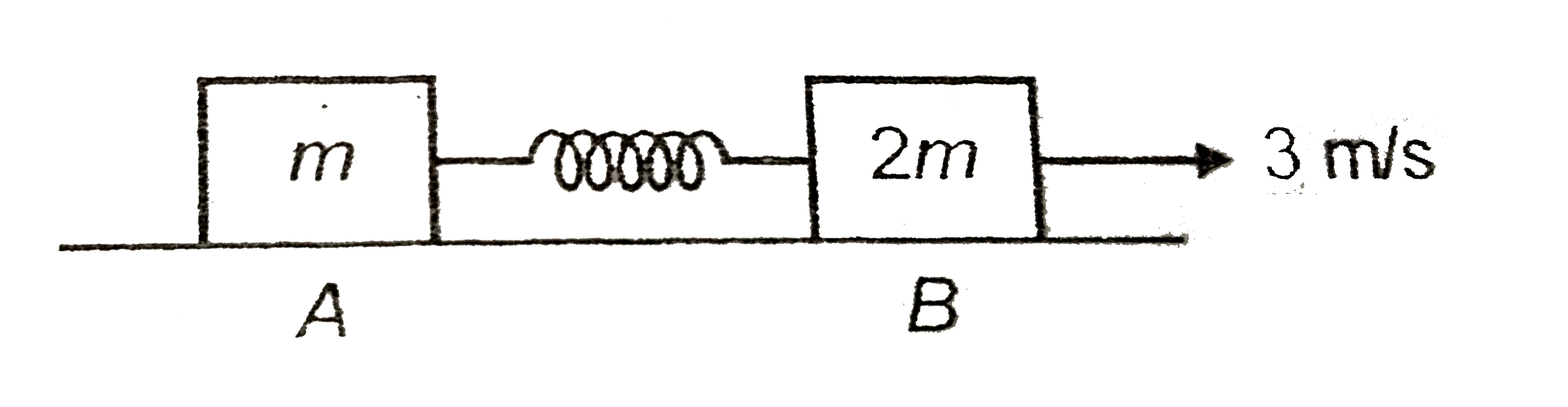
View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View Solution
