A uniform rod of length L and density ρ is being pulled along a smooth floor with a horizontal acceleration α (see Fig.) The magnitude of the stress at the transverse cross-section through the mid-point of the rod is……..
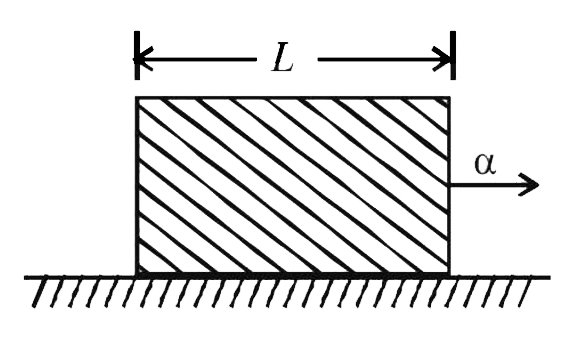
The correct Answer is:(ρLα2)
(ρLα2)
Let A be area of cross - section of the rod.

Mass of half rod , m= volume× density =(L2A)ρ
FBD of rod at mid - point

∴T=mα=(L2Aρα)∴Stress=TA=12ραL
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Main (Archive) Level - 2 (TRUE /FALSE TYPE)
3 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (NUMBERICAL VALUE TYPE)
7 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
A uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
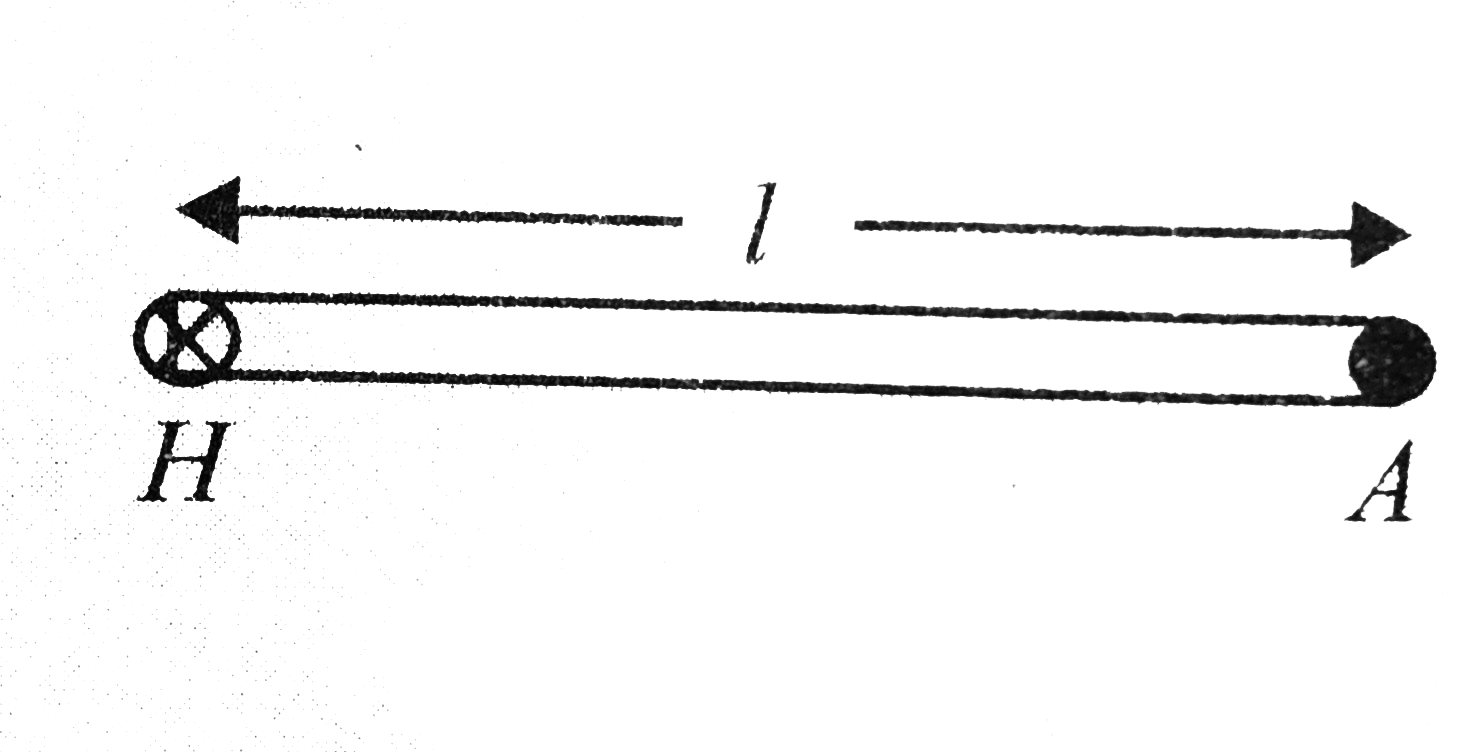
View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
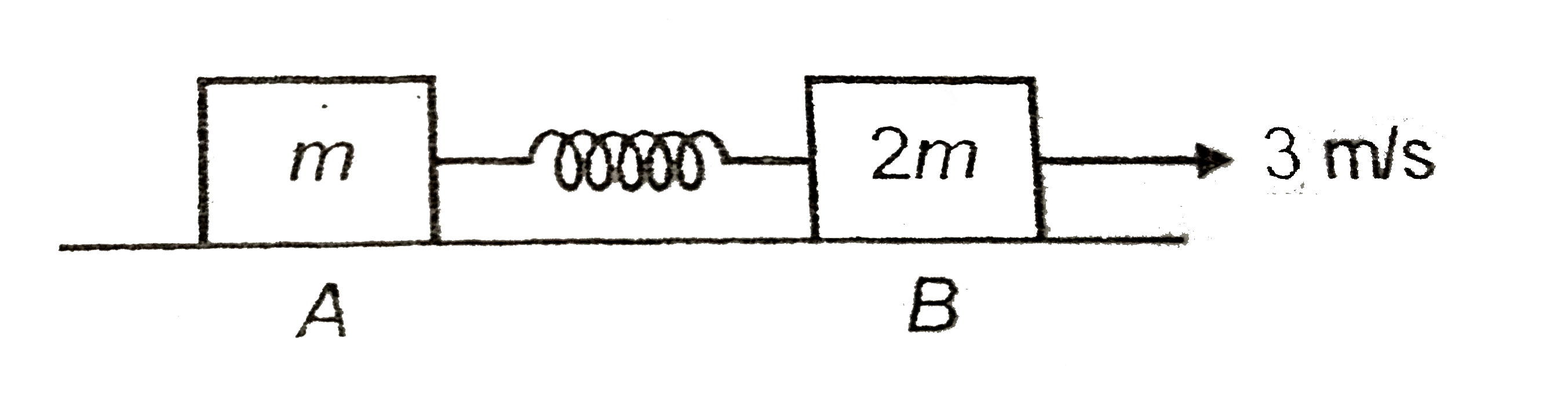
View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionA uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
View SolutionA uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
View SolutionA uniform rod of mass m and length L is kept on a horizontal table with L4 length on the table as shown in figure. As the string attached to the end B is cut, the angular acceleration of the rod about point C will be
_PHY_E05_242_Q01.png)
View Solution
