When a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
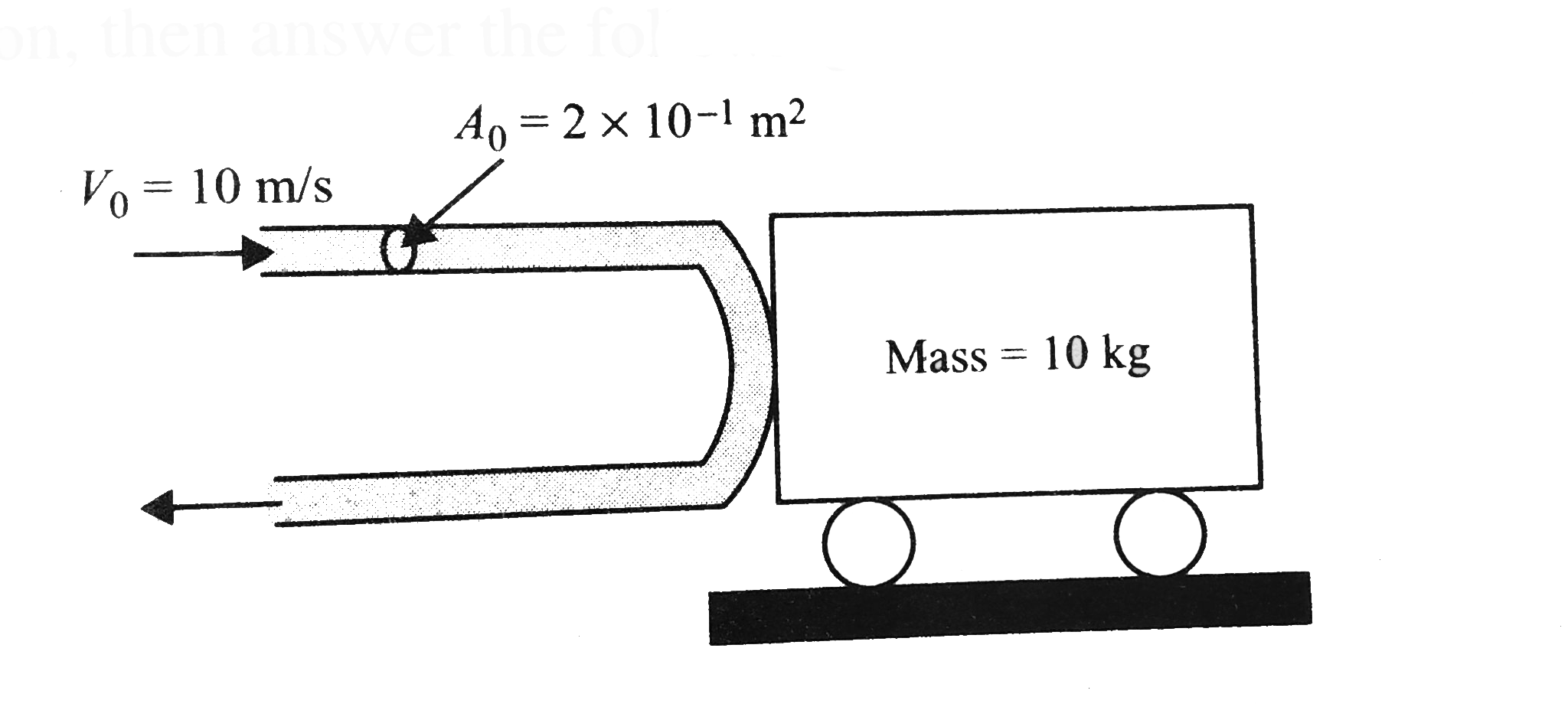
![When a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum. F=(rhoAV(0))V(0)-(rhoAV(0))V(0)costheta=rhoAV(0)^(2)[1-costheta] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u. Then the above equation becomes F=rhoA(V(0)-u)^(2)[1-costheta] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following. Given that cross sectional area of jet =2xx10^(-4)m^(2) velocity of jet V(0)=10m//s density of liquid =1000kg//m^(3) ,mass of cart M=10 kg. The time at which velocity of cart becomes 2 m/s is equal to](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_VOL2_C04_E01_201_Q01.png)
F=(ρAV0)V0−(ρAV0)V0cosθ=ρAV20[1−cosθ] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u. Then the above equation becomes <br>F=ρA(V0−u)2[1−cosθ] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
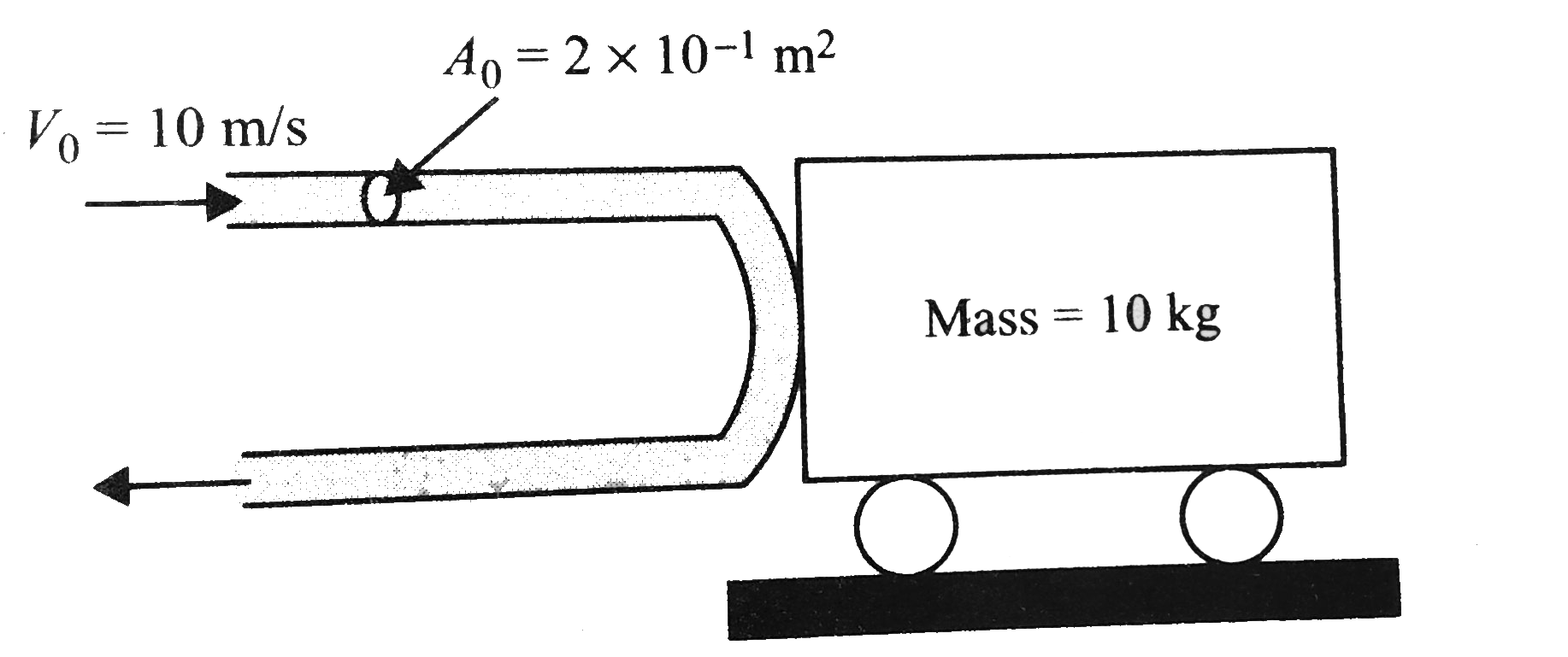
Given that cross sectional area of jet =2×10−4m2 velocity of jet V0=10m/s density of liquid =1000kg/m3 ,mass of cart M=10kg.
The time at which velocity of cart becomes 2ms is equal to
1.6s
2s
3.2s
4s
The correct Answer is:A
From eqn i 1V0−u−1V0=4t100
⇒18+110=4t100
⇒280=4t100
t=1.6s
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
When a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
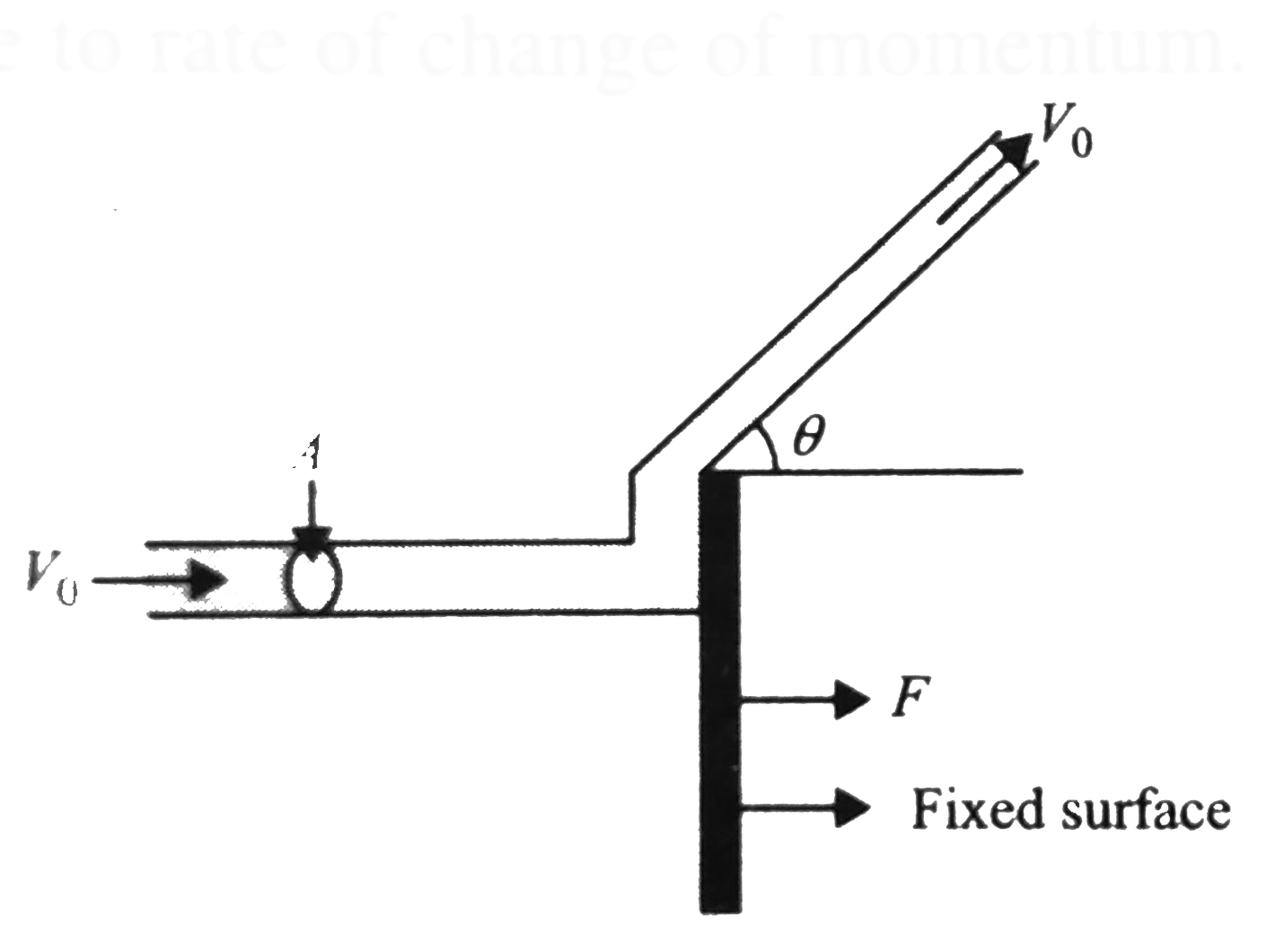
F=(ρAV0)V0−(ρAV0)V0cosθ=ρAV20[1−cosθ] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u. Then the above equation becomes <br>F=ρA(V0−u)2[1−cosθ] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
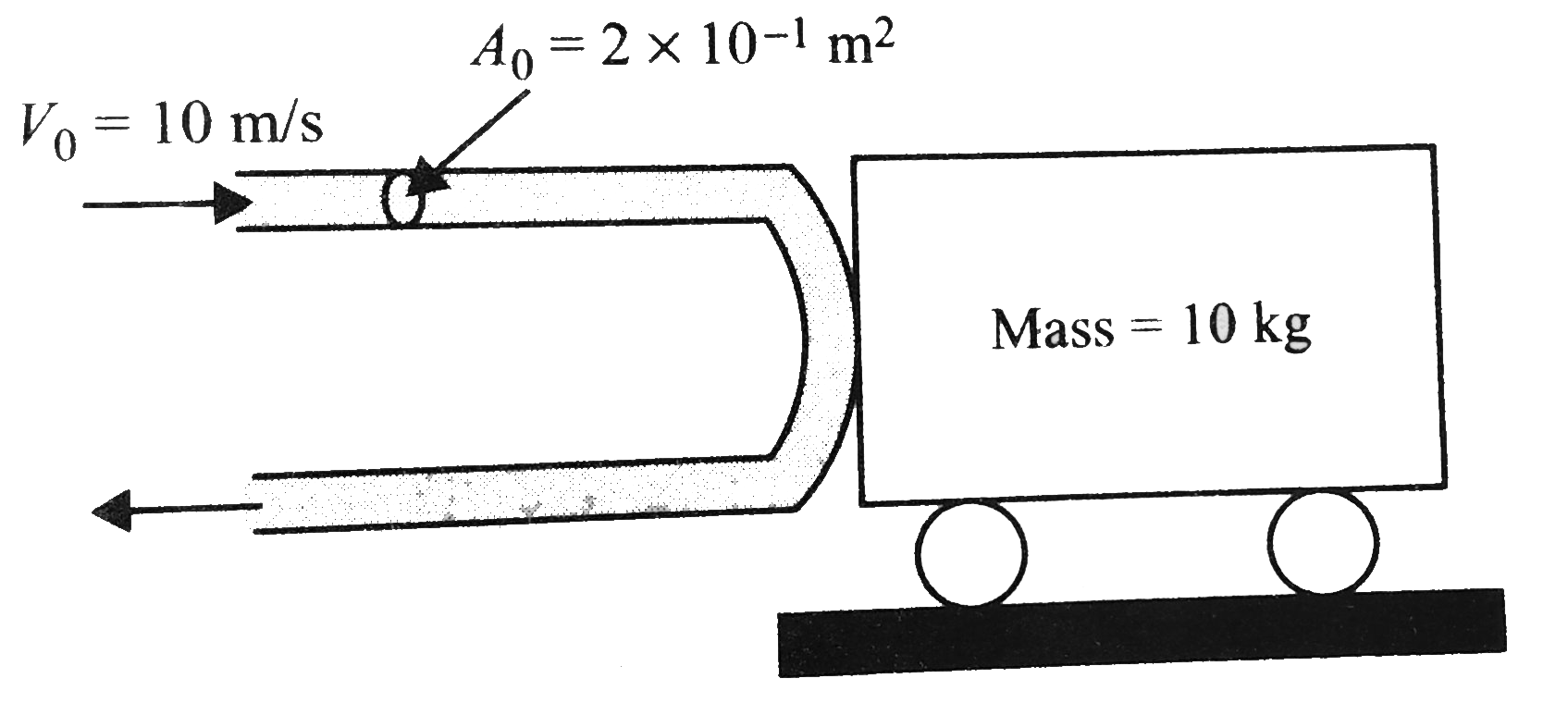
Given that cross sectional area of jet =2×10−4m2 velocity of jet V0=10m/s density of liquid =1000kg/m3 ,mass of cart M=10kg.
The power supplied to the cart when its velocity becomes 5m/s is equal to
View SolutionWhen a jet of liquid strikes a fixed or moving surface, it exerts thrust on it due to rate of change of momentum.
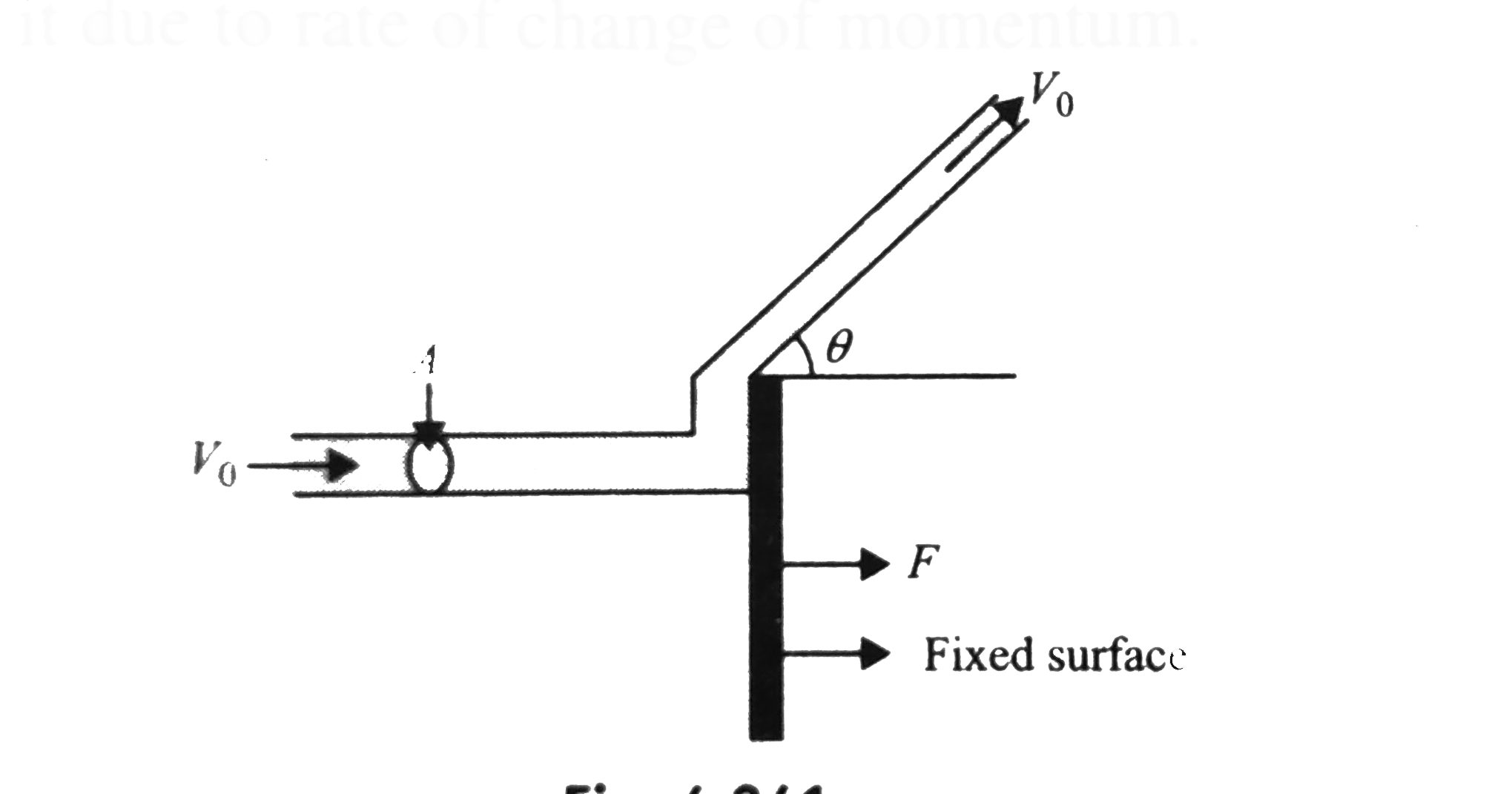
F=(ρAV0)V0−(ρAV0)V0cosθ=ρAV20[1−cosθ] If surface is free and starts moving due to thrust of the liquid, then at any instant, the above equation gets modified based on relative change of momentum with respect to surface. Let, at any instant, the velocity of surface be u. Then the above equation becomes <br>F=ρA(V0−u)2[1−cosθ] Based on the above concept, as shown in the following figure, if the cart is frictionless and free to move in the horizontal direction, then answer the following.
Given that cross sectional area of jet =2×10−4m2 velocity of jet V0=10m/s density of liquid =1000kg/m3 ,mass of cart M=10kg.
Initially (l=0) the force on the cart is equal to
View SolutionA spherical rain drop evaporates at a rate proportional to its surface area at any instant t. The differential equation giving the rate of change of the radius of the rain drop is _____
View SolutionA spherical rain drop evaporates at a rate proportional to its surface area at any instant t. The differential equation giving the rate of change of the radius of the rain drop is _____
View SolutionA conducting rod AB of length l is projected on a frictionless frame PSRQ with velocity v0 at any instant. The velocity of the rod after time t is
View SolutionWedge of 10kg is free to move on horizontal surface. At the given instant, acceleration of wedge is (string and pulleys are ideal)
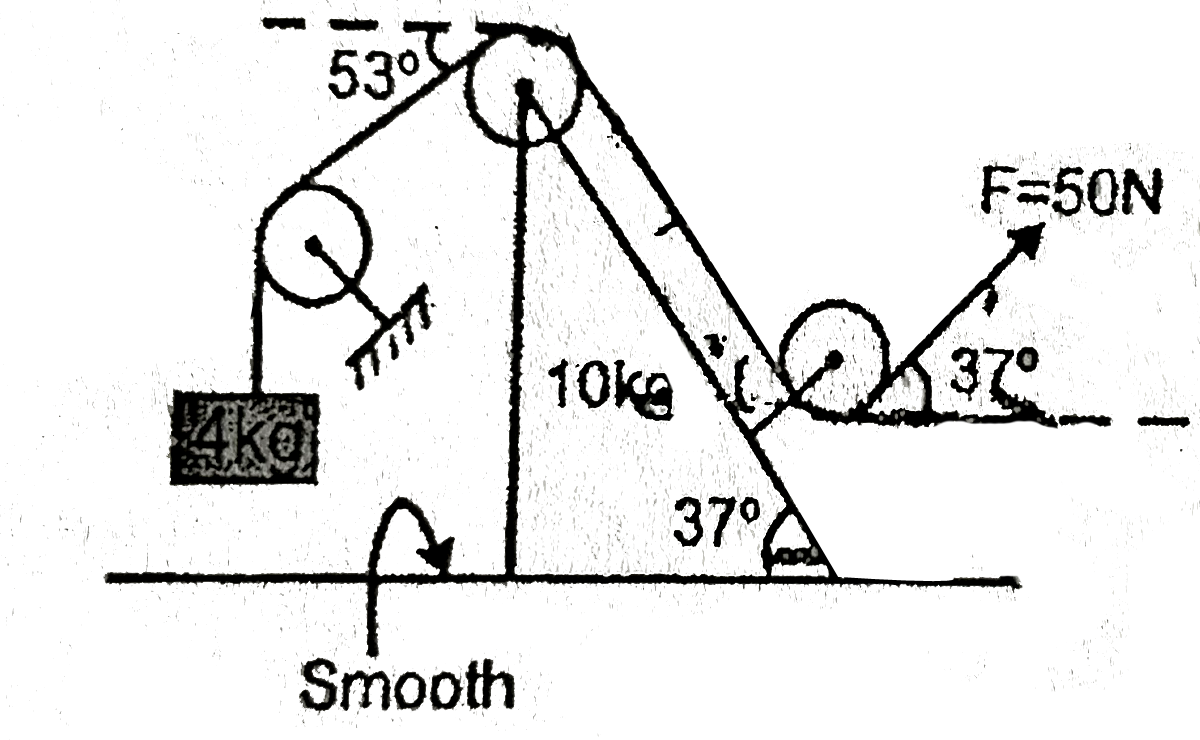View SolutionThe volume of a spherical balloon is increasing at the rate of 20 cm3/sec . Find the rate of change of its surface area at the instant when radius is 5 cm.
View SolutionA uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
View SolutionThe momentum of a particle of mass of m moving with a velocity v is p= mv. What is the rate of change of momentum ? Assume that m is constant .
View SolutionAt the instant t=0, a force F=kt (k is a constant) acts on a small body of mass m resting on a smooth horizontal surface. The time, when the body leaves the surface is
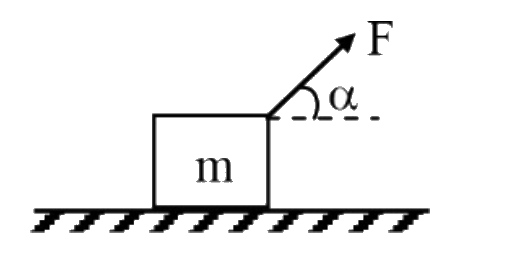View Solution