Figure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the height h2 of the water in the long tube above top initially.
3p0ρg−h03
2p0ρg−h02
p0ρg−h0
p02ρg−2h0
The correct Answer is:C
2P0=(h2+h0)ρg+p0
(since liquids at the same level have the same pressure)
P0=h2ρg+h0ρg
h2ρg=P0−h0ρg
h2=P0ρg−h0ρgρg=P0ρg−h0
KE of the water = Pressure energy of the water at that layer
12mV2=m×Pρ
V2=2Pρ=2ρ[P0+ρg(h1−h2)]
V=[2ρ{P0+ρg(h1−h0)}]12
We know 2P0+ρg(h1−h0)=P0=ρgX
⇒X=P0ρg+(h1−h0)=h2+h1
i.e., X is h1 metre below the top or X is −h1 above the top.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Figure shows a large closed cylindrical tank containing water, Initially the air trapped above the water surface has a height h0and pressure 2p0 where p0is the atmospheric pressure. There is a hole in the wall of tank at a depth h1below the top from which water comes out. A long vertical tube is connected as shown. (a) Find the height h2 of the water in the long tube above the top initially. (b) Find the speed with which water comes out of hole.(c)Find the height of the water in the long tube above the top when the water stops coming out of the hole.

View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the height of the water in the long tube above the top when the water stops coming out of the hole.
View Solution
Knowledge Check
The height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
AHBH2C3H2D√3H2The pressure P1 at the top of a dam and P2 at a depth h from the top inside water (density ρ) are related as :
AP1>P2BP1=P2CP1−P2=hρgDP2−P1=hρg
Figure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the speed with which water comes out of the hole
View SolutionThe pressure at the bottom of an open tank of water is 3p where p is the atmospheric pressure. If the water is drawn out till the level of water remains one fifth, the pressure at the bottom of the tank will now be
View SolutionThe pressure at the bottom of a tank of water is 2P, where P is the atmospheric pressure.If the water is drawn out till the level of water is lowered by one half of initial,the pressure at the bottom of the tank will now be
View SolutionFigure shows a capillary tube of radius r dipped into water. If the atmosphere pressure is P0, the pressure at point A is
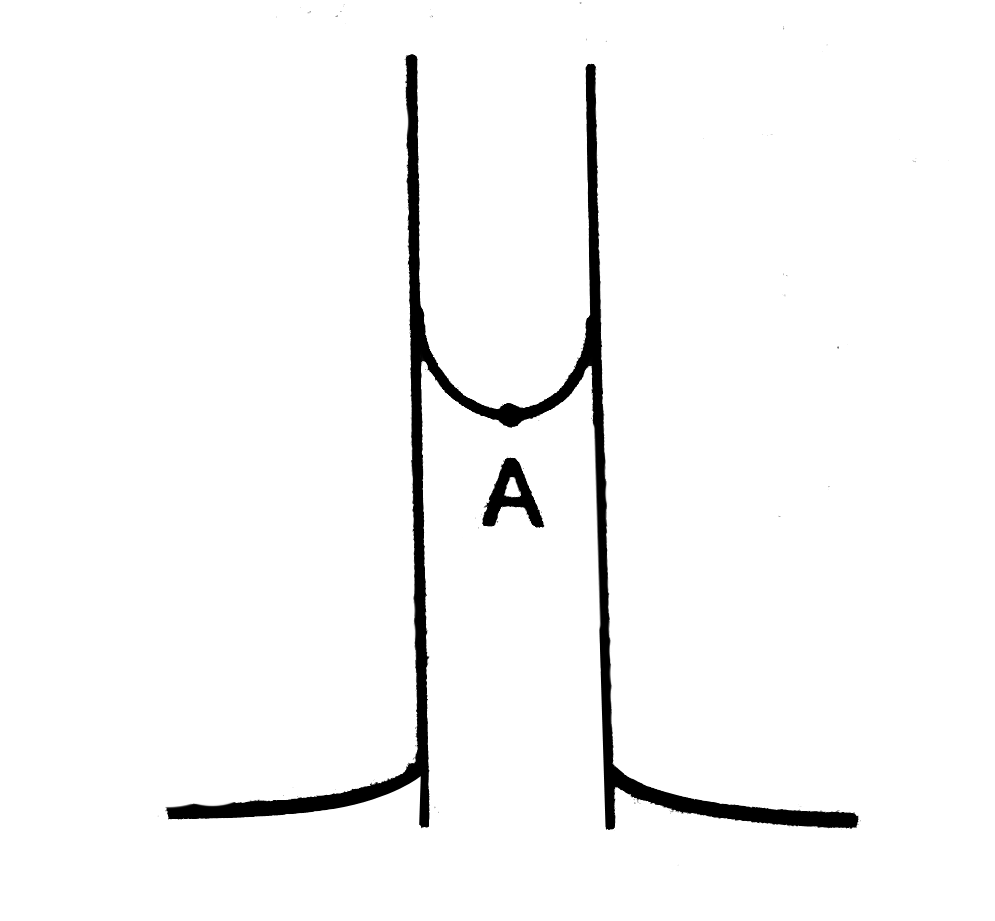
View SolutionP is the atmospheric pressure and the pressure at the bottom of a tank of water is 3P. If the water is drawn out to lower the level of water by one fifth, then the pressure at the bottom of the tank will be
View SolutionThe pressure at the bottom of a water tank is 4 P, where P is .atmospheric pressure. If water is drawn out till the water level decreases by —35th, then pressure at the bottom of the tank is
View Solution
