The difference of pressure between two points along a horizontal pipe through which water is flowing is of . If due to non-uniform cross section the speed of flow at a point of greater cross section is , speed of flow at the other point is
less than
not affected by non-uniform cross section
greater than
The correct Answer is:A, D
To solve the problem, we will use Bernoulli's equation and the concept of fluid flow in a pipe. Here are the steps to find the speed of flow at the other point in the horizontal pipe:
Step 1: Understand the Given Information
We are given:
- Pressure difference (ΔP) between two points = 14 cm of Hg
- Speed of flow at the point of greater cross-section (V1) = 60 cm/s
Step 2: Convert Pressure Difference to SI Units
We need to convert the pressure difference from cm of Hg to Pascals (Pa).
1. The density of mercury (ρ_Hg) = 13,600 kg/m³.
2. The acceleration due to gravity (g) = 9.81 m/s².
3. Convert 14 cm of Hg to meters: 14 cm = 0.14 m.
Using the formula for pressure:
ΔP=ρHg⋅g⋅h
ΔP=13600kg/m3⋅9.81m/s2⋅0.14m
Calculating ΔP:
ΔP=13600⋅9.81⋅0.14
ΔP≈18850.4Pa
Step 3: Apply Bernoulli's Equation
For a horizontal pipe, Bernoulli's equation states:
P1+12ρV21=P2+12ρV22
Rearranging gives us:
P1−P2=12ρV22−12ρV21
ΔP=12ρ(V22−V21)
Step 4: Substitute Known Values
We know ΔP and V1. We can express V2 in terms of V1:
18850.4=12⋅1000⋅(V22−(0.6)2)
(Note: The density of water (ρ) = 1000 kg/m³, and V1 = 60 cm/s = 0.6 m/s)
Step 5: Solve for V2
Rearranging the equation:
18850.4=500(V22−0.36)
37.7=V22−0.36
V22=37.7+0.36
V22=38.06
Taking the square root:
V2=√38.06
V2≈6.17m/s
Step 6: Convert to cm/s
Convert V2 back to cm/s:
V2≈617cm/s
Final Answer
The speed of flow at the other point is approximately 617 cm/s.
---
We are given:
- Pressure difference (ΔP) between two points = 14 cm of Hg
- Speed of flow at the point of greater cross-section (V1) = 60 cm/s
We need to convert the pressure difference from cm of Hg to Pascals (Pa).
1. The density of mercury (ρ_Hg) = 13,600 kg/m³.
2. The acceleration due to gravity (g) = 9.81 m/s².
3. Convert 14 cm of Hg to meters: 14 cm = 0.14 m.
ΔP=ρHg⋅g⋅h
ΔP=13600kg/m3⋅9.81m/s2⋅0.14m
ΔP=13600⋅9.81⋅0.14
ΔP≈18850.4Pa
For a horizontal pipe, Bernoulli's equation states:
P1+12ρV21=P2+12ρV22
P1−P2=12ρV22−12ρV21
ΔP=12ρ(V22−V21)
We know ΔP and V1. We can express V2 in terms of V1:
18850.4=12⋅1000⋅(V22−(0.6)2)
(Note: The density of water (ρ) = 1000 kg/m³, and V1 = 60 cm/s = 0.6 m/s)
Rearranging the equation:
18850.4=500(V22−0.36)
37.7=V22−0.36
V22=37.7+0.36
V22=38.06
V2=√38.06
V2≈6.17m/s
Convert V2 back to cm/s:
V2≈617cm/s
The speed of flow at the other point is approximately 617 cm/s.
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Linked Comprehension
Explore 43 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICS ENGLISHChapter:FLUID MECHANICSExercise:Single Correct
Explore 95 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
Current is flowing through a wire of non-uniform cross section. Cross section of wire at A is les than the cross section of wire at B. Then match the following
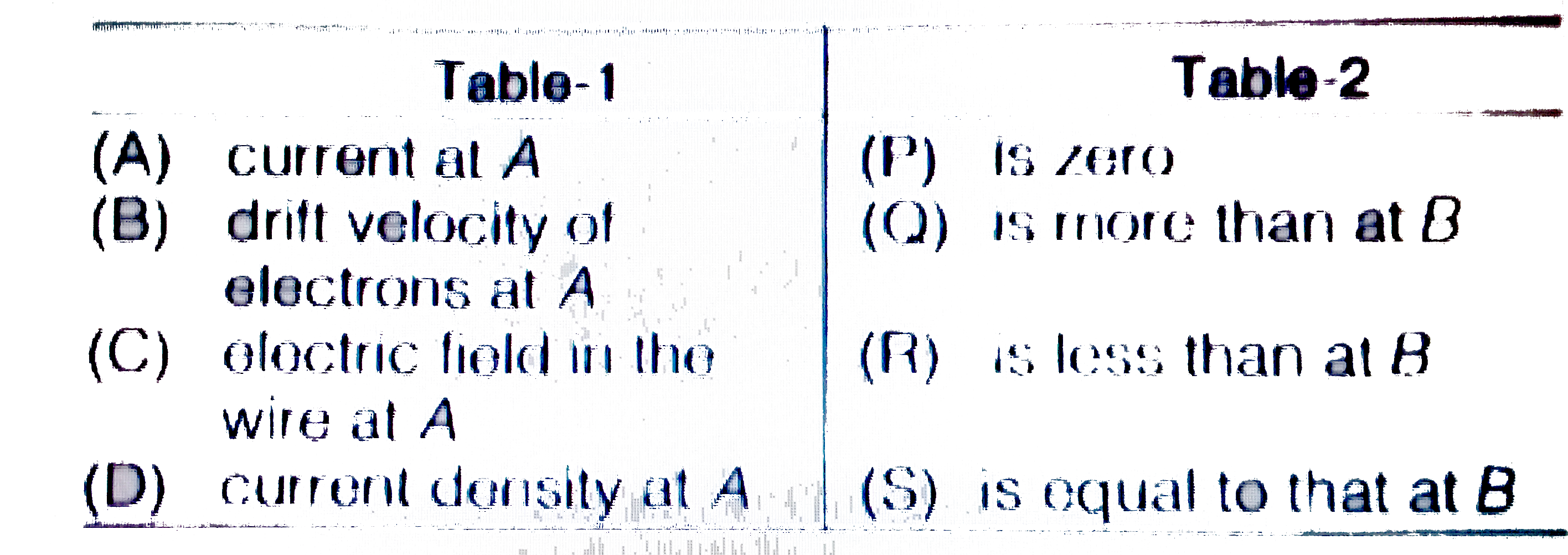
View SolutionA stready current i is flowing through a conductor of uniform cross-section. Any segment of the conductor has
View SolutionWater is flowing steadily through a horizontal pipe of non - uniform cross - section . If the velocity of water cross - section is 0.02m2 is 2m/s , what is the velocity of water at another point where the cross - section is 0.01m2 ?
View SolutionA steady current is set up in a metalic wire of non- uniform cross-section. How is the rate of flow free electrons related
View SolutionA liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.

View SolutionWhen a steady current flows through a metal conductor of non-uniform cross-section , then drift velocity is
View SolutionA liquid is flowing in a horizontal pipe of non-uniform cross section. Which of the following quantities may remain unchanged with respect to time?
View SolutionThe water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionA non viscous inconpressible liquid is flowing from a horizontal pipe of non-uniform cross section as shown, Choose the correct option
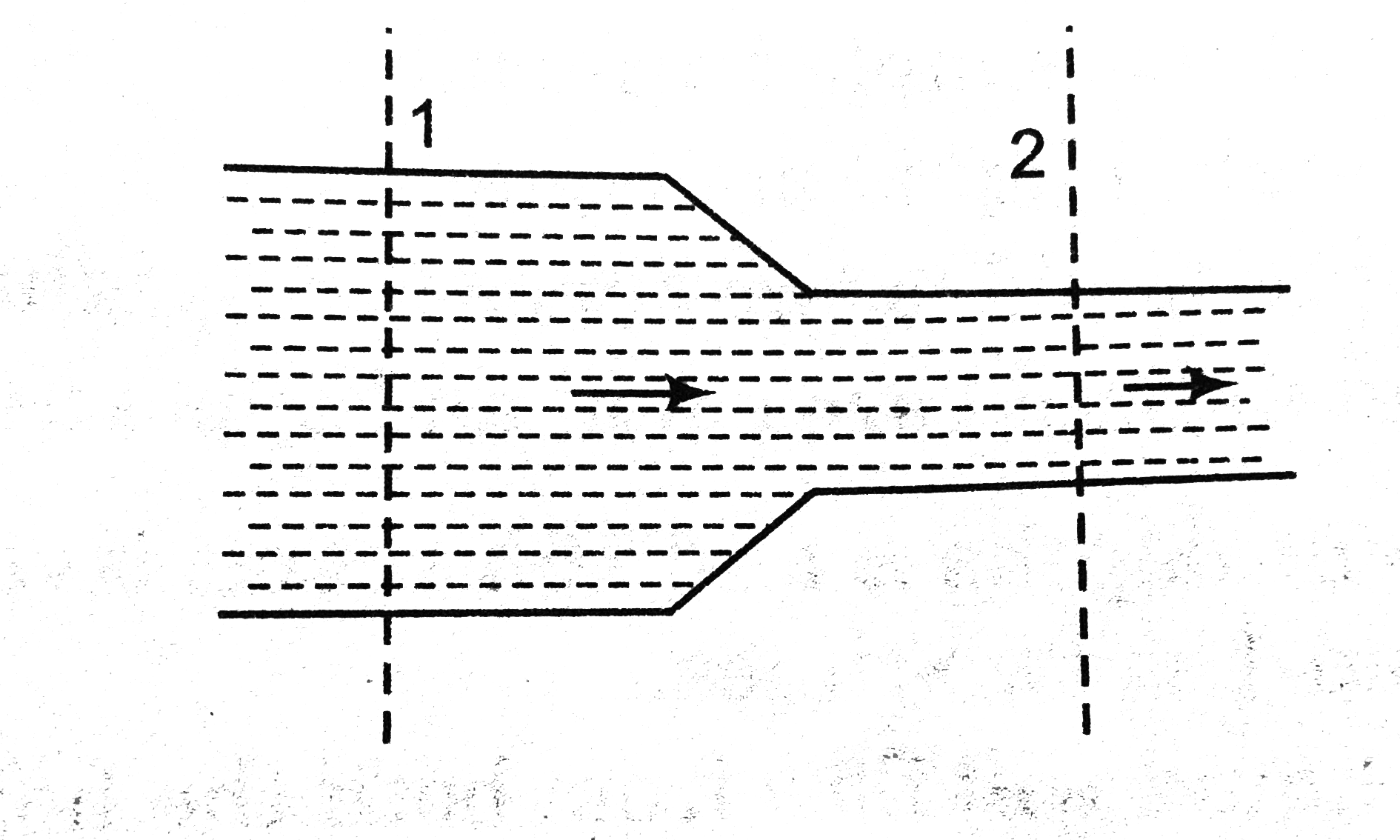
View SolutionWater flows along horizontal pipe whose cross-section is not constant. The pressure is 1 cm of Hg, where the velocity is 35 cm/s . At a point where the velocity is 65cm/s then pressure will be
View Solution