Question

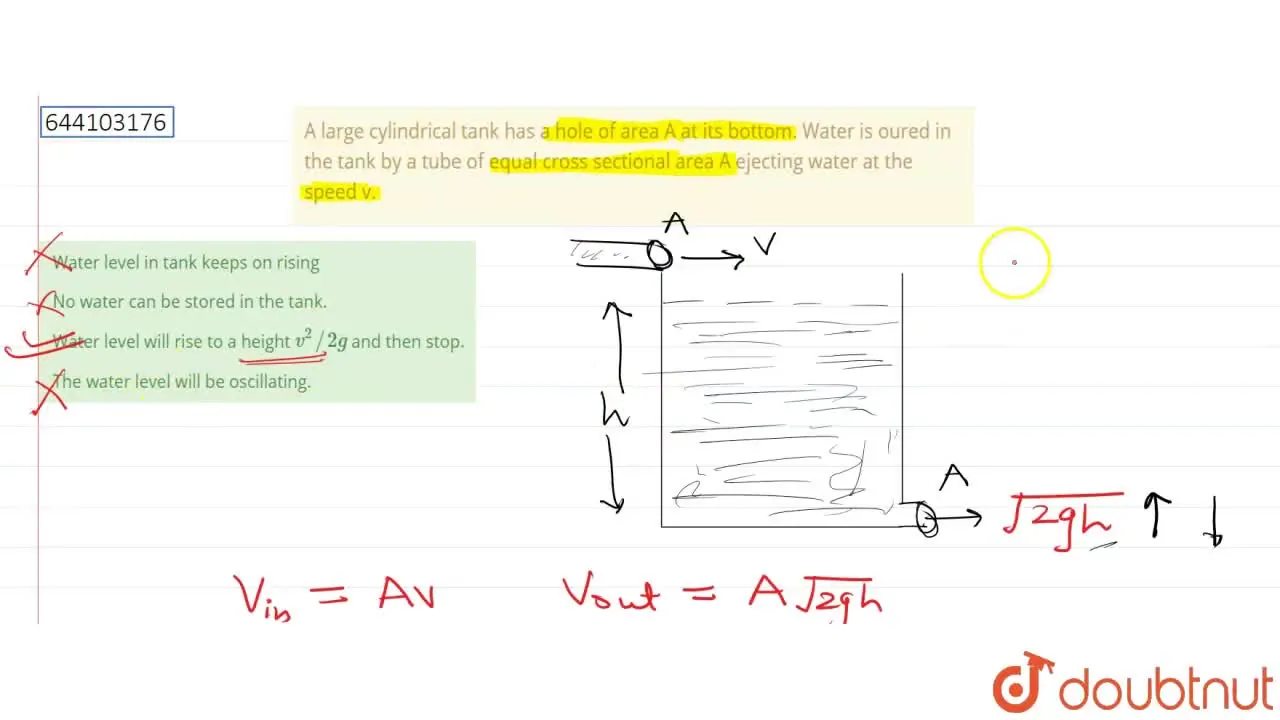
A large cylindrical tank has a hole of area A at its bottom. Water is oured in the tank by a tube of equal cross sectional area A ejecting water at the speed v.

Options

A. Water level in tank keeps on rising
B. No water can be stored in the tank.
C. Water level will rise to a height `v^(2)//2g` and then stop.
D. The water level will be oscillating.

Answer

C

Explanation

To solve the problem, we need to analyze the flow of water into and out of the cylindrical tank. We will derive the conditions under which the water level remains constant, rises, or falls.

1. Identify the Variables:
- Let \( A \) be the cross-sectional area of the hole at the bottom of the tank and the tube.
- Let \( v \) be the speed of water being poured into the tank.
- Let \( h \) be the height of water in the tank.
- The speed of water exiting the hole at the bottom of the tank can be determined using Torricelli's theorem, which states that the speed \( v_{out} \) of fluid flowing out of an orifice under the influence of gravity is given by:
\( v_{out} = \sqrt{2gh} \)

2. Calculate the Volumes:
- The volume of water entering the tank per unit time (inflow) is:
\( V_{in} = A \cdot v \)
- The volume of water exiting the tank per unit time (outflow) is:
\( V_{out} = A \cdot v_{out} = A \cdot \sqrt{2gh} \)

3. Establish the Condition for Steady State:
- For the water level in the tank to remain constant, the inflow must equal the outflow:
\( V_{in} = V_{out} \)
- Substituting the expressions for inflow and outflow:
\( A \cdot v = A \cdot \sqrt{2gh} \)
- We can simplify this by canceling \( A \) (assuming \( A \neq 0 \)):
\( v = \sqrt{2gh} \)

4. Square Both Sides:
- Squaring both sides gives:
\( v^2 = 2gh \)

5. Solve for Height \( h \):
- Rearranging the equation to find \( h \):
\( h = \frac{v^2}{2g} \)

6. Analyze the Scenarios:
- If \( v > \sqrt{2gh} \), then \( V_{in} > V_{out} \) and the water level will rise.
- If \( v < \sqrt{2gh} \), then \( V_{in} < V_{out} \) and the water level will fall.
- If \( v = \sqrt{2gh} \), then \( V_{in} = V_{out} \) and the water level will remain constant at \( h = \frac{v^2}{2g} \).

7. Conclusion:
- The water level will rise to a height of \( \frac{v^2}{2g} \) and then stabilize at this height, where the inflow equals the outflow.

Final Answer:
The water level will rise to a height of \( \frac{v^2}{2g} \) and then stop.