Figure shows a stream of fluid emerging from a tube in the base of an open tank. Obtain an expression for 'y' in terms of θ and 'h'. Can exceed 'h'?
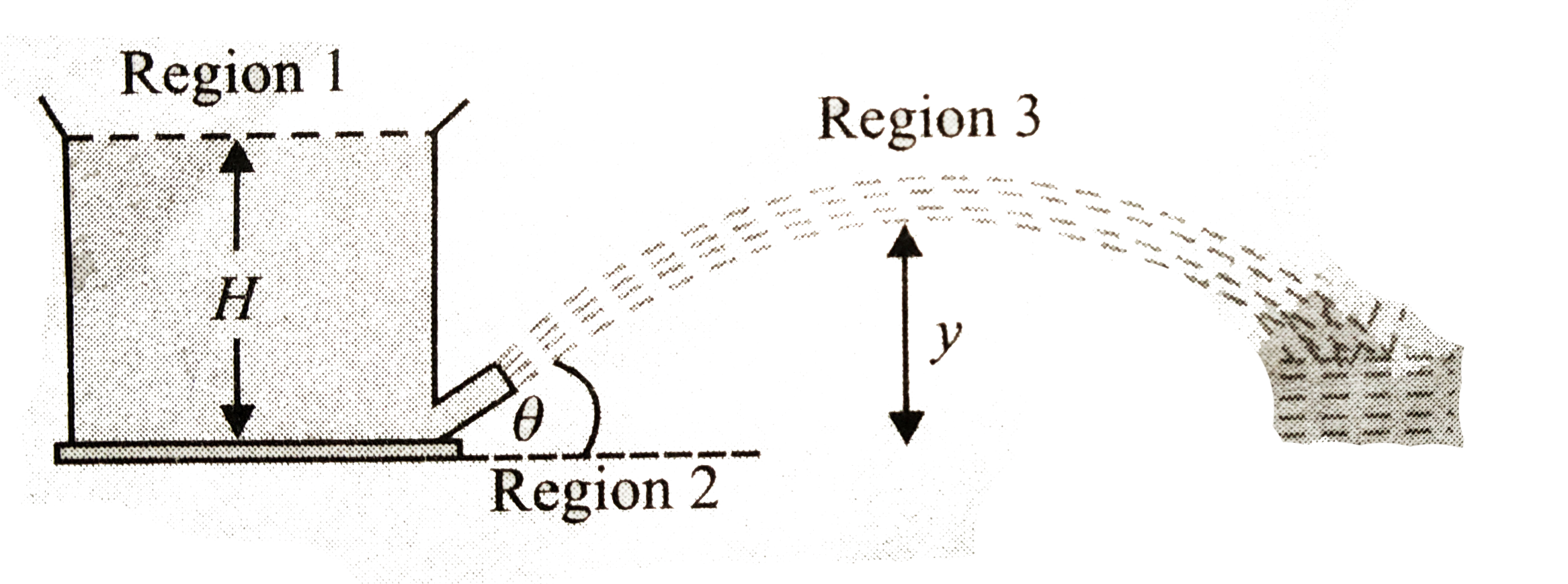
We apply Bernoullis equation between points 2 and 3.
P2+12ρv22+ρgy2=P3+12ρv23+ρgh3
Patm+12ρv22+0=Patm+12ρv23+ρgy………i
As both the points are open the atmosphere P2=P3=Patm
Taking ground level as reference level potential energy at point 2 is zero.
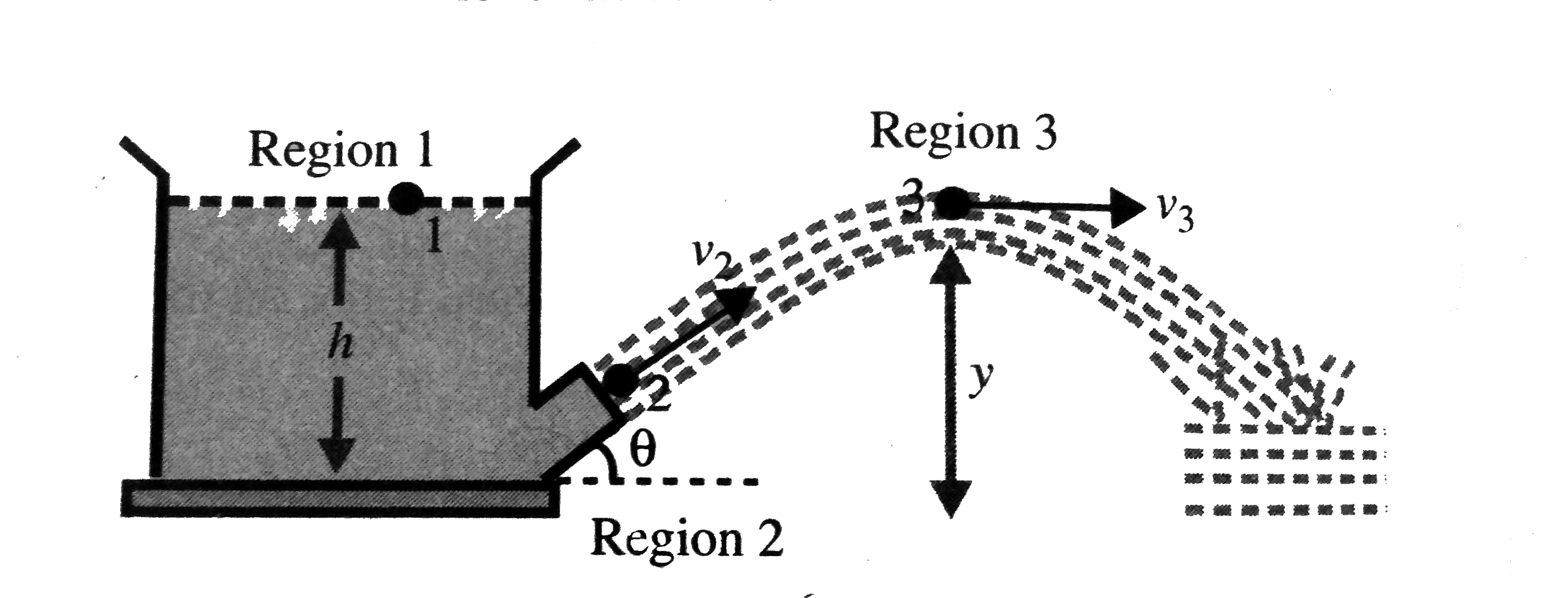
Since there is no horizontal acceleration v3=v2cosθ.
From eqn i we obtain
y=12(v22−v22cos2θ)g=12v22sin2θg....ii
From Torricelli's theroem v22=2gh
That, y=sin2θ
y=h when sinθ=1, i.e. θ=90∘ therefore y can never exceed h.
Related Playlists
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective25videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Single Correct95videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.310videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
Water falls from a tap with A0=4m2, A=1m2 and h=2 m, then velocity v is
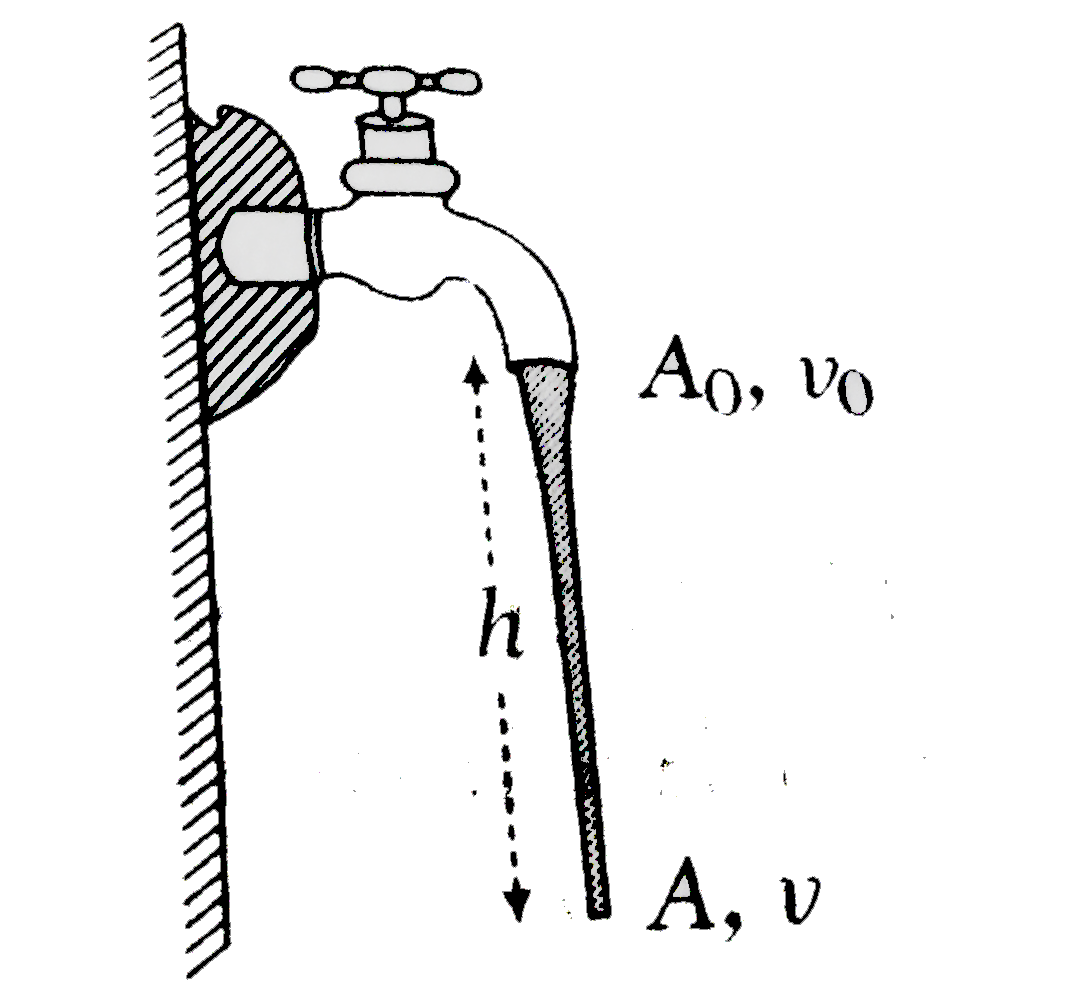 View Solution
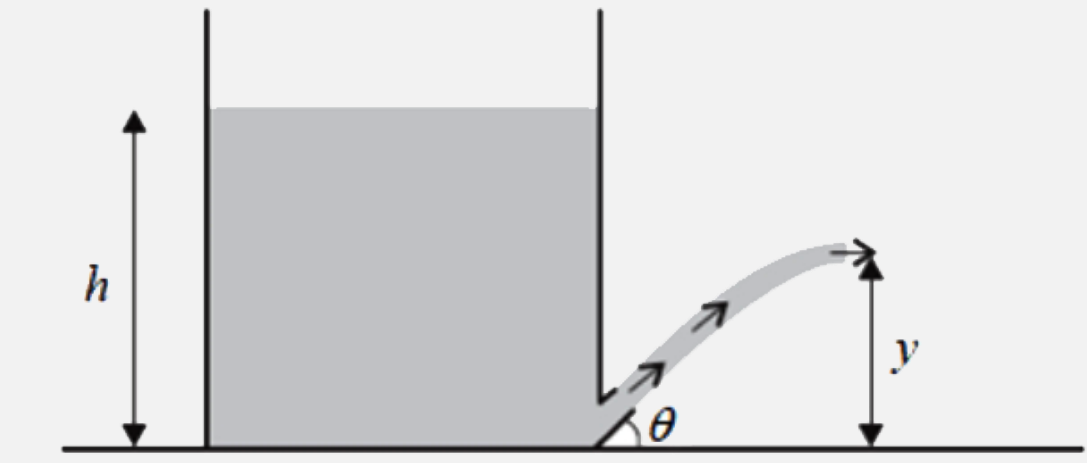
View SolutionA stream of non-viscous liquid emerges from a very short outlet tube at the base of a large . Open tank , in which the depth of liquid is h. The tube is at a fixed angle θ to the ground as shown in the figure. The maximum height of the stream y is
 View Solution
View SolutionThe height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
View SolutionState Hooke's law. A metallic wire of Young's modulus Y is stretched by suspending a load from it. If the linear strain produced in it is μ, obtain an expression for the elastic potential energy, in terms of Y and μ , stored in unit volume of the wire.
View SolutionThe area of a parallelogram is y cm2 and its height is h cm. The base of another parallelogram is x cm more than the base of the first parallelogram and its area is twice the area of the first. Find, in terms of y, h and x, the expression for the height of the second parallelogram.
View SolutionIf Planck's constant (h) and speed of light in vacuum (c ) are taken as two fundamental quantites, which on of the following can, in addition, be taken to express length, mass and time in terms of the three chosen fundamental quantities ?
View Solution
The graphs above show the complete functions h and k. which one of the following expresses k(x) in terms of h(x)?View SolutionA liquid is filled in a container to a height H. A small hole is opened in the side of the container a height h below the surface of the liquid. The distance L from the bottom of the container of the point where the stream of liquid leaving the container meets the ground is :
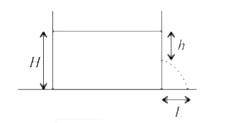 View Solution
View SolutionThe circumference of nth orbit in H-atom can be expressed in terms of deBroglie wavelength λ as :
View SolutionT=R2r2√2hg
Suppose an open cylindrical tank has a round drain with radius t in the bottom of the tank. When the tank is filled with water to a depth of h centimeters, the time it takes for all the water to drain from the tank is given by the formula above, where R is the radius of the tank (in centimeters) and g=980cm/s2 is the acceleration due to gravity. Suppose such a tank has a radius of 2 meters and is filled to a depth of 4 meters. About how many minutes does it take to empty the tank if the drain has a radius of 5 centimeters? (1 meter=100 centimeter).View Solution


