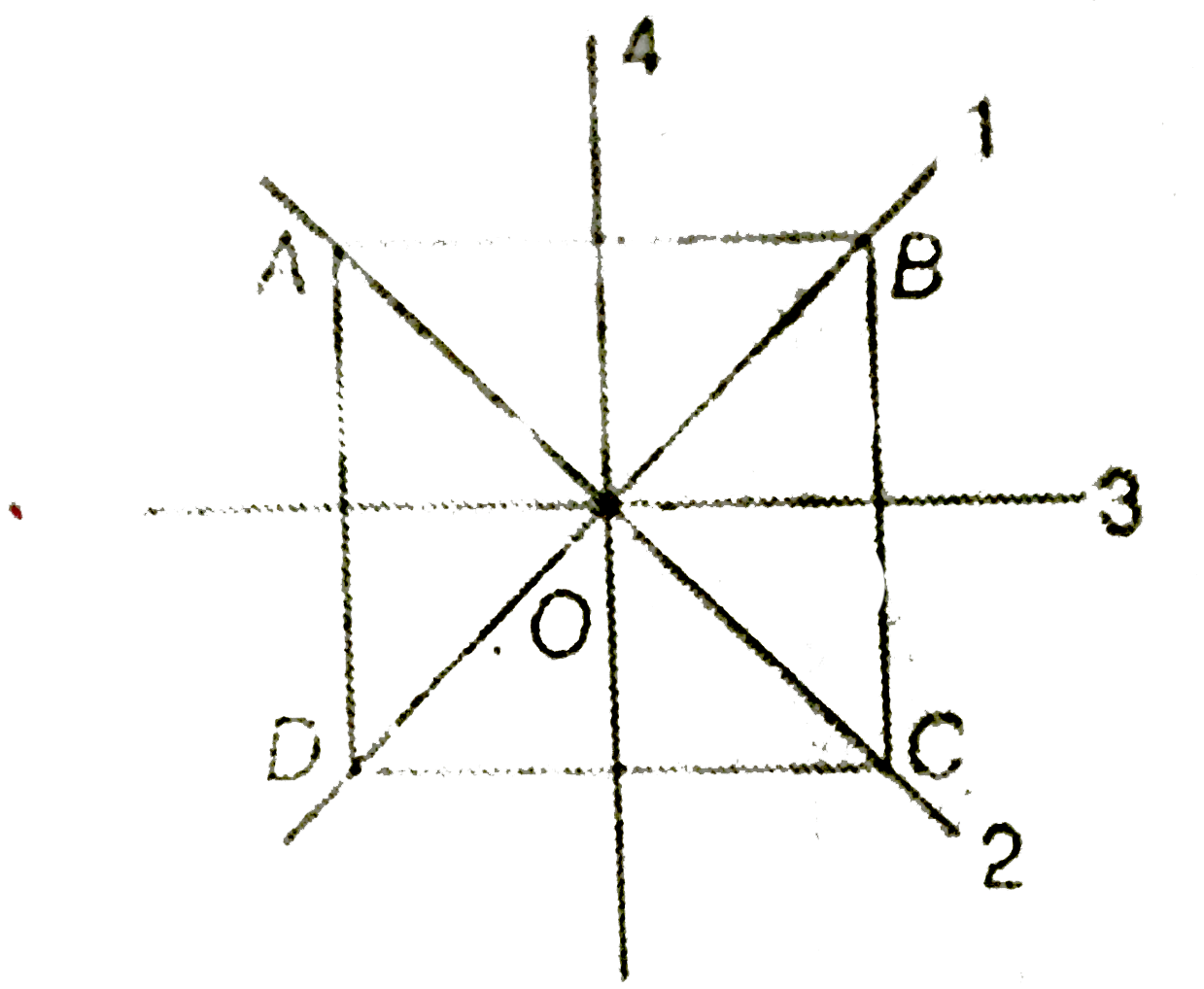
Let I be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle $θ$ with AB. The moment of inertia of the plate about the axis CD is then equal to

A

$I$

B

$I {sin}^{2} θ$

C

$I {cos}^{2} θ$

D

$I {cos}^{2} (\frac{θ}{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$A' B' ⊥ A B$ and $C'' D' ⊥ C D$
From symmetry $I_{A B} = I_{A' B}$ and $I_{C D} = I_{C D}$
From theorem of perpendicular axis

$I_{z z} = I_{A B} I_{A' B'} = I_{C D} + I_{C D'}$
$\Rightarrow 2 I_{A B} = 2 I I_{C D}$
$I_{A B} = I_{C D}$
Alternative method:
The relation between $I_{A B}$ and $I_{C D}$ should be true for all values of $θ$
At $θ = I_{C D} = I_{A B}$
Similarly at $θ = \frac{π}{2}$
$I_{C D} = I_{A B}$ (By symmetry)
Keeping these things in mind, option a is correct.

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Ler l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle $θ$ with AB. The moment of inertia of the plate about the axis CD is then equal to
A $I$
B $I {sin}^{2} θ$
C $I {cos}^{2} θ$
D $I {cos}^{2} (\frac{θ}{2})$ .

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 2-MCQ_TYPE

Home
Ask Doubt
Profile