Two discs A and B are mounted co-axially one vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The rotation x1/x2 is.
2
12
√2
1√2
The correct Answer is:C
To solve the problem, we will use the principle of conservation of energy, which states that the change in rotational kinetic energy of the discs is equal to the change in potential energy stored in the springs.
1. Identify the Moments of Inertia:
- Let the moment of inertia of disc A be I.
- The moment of inertia of disc B is given as 2I.
2. Determine the Initial Angular Velocities:
- Disc A is given an initial angular velocity of 2ω.
- Disc B is given an initial angular velocity of ω.
3. Calculate the Rotational Kinetic Energy for Each Disc:
- For disc A, the rotational kinetic energy KA is given by:
KA=12I(2ω)2=12I⋅4ω2=2Iω2
- For disc B, the rotational kinetic energy KB is given by:
KB=12(2I)ω2=Iω2
4. Relate the Kinetic Energy to the Potential Energy of the Springs:
- The potential energy stored in the spring for disc A when compressed by distance x1 is:
PEA=12kx21
- The potential energy stored in the spring for disc B when compressed by distance x2 is:
PEB=12kx22
5. Set Up the Energy Conservation Equations:
- For disc A:
KA=PEA⟹2Iω2=12kx21(1)
- For disc B:
KB=PEB⟹Iω2=12kx22(2)
6. Divide Equation (1) by Equation (2):
2Iω2Iω2=12kx2112kx22
Simplifying gives:
2=x21x22
7. Solve for the Ratio x1x2:
x21x22=2⟹x1x2=√2
Final Answer:
The ratio of the distances the springs are compressed is:
x1x2=√2
- Let the moment of inertia of disc A be I.
- The moment of inertia of disc B is given as 2I.
- Disc A is given an initial angular velocity of 2ω.
- Disc B is given an initial angular velocity of ω.
- For disc A, the rotational kinetic energy KA is given by:
KA=12I(2ω)2=12I⋅4ω2=2Iω2
- For disc B, the rotational kinetic energy KB is given by:
KB=12(2I)ω2=Iω2
- The potential energy stored in the spring for disc A when compressed by distance x1 is:
PEA=12kx21
- The potential energy stored in the spring for disc B when compressed by distance x2 is:
PEB=12kx22
- For disc A:
KA=PEA⟹2Iω2=12kx21(1)
- For disc B:
KB=PEB⟹Iω2=12kx22(2)
2Iω2Iω2=12kx2112kx22
Simplifying gives:
2=x21x22
x21x22=2⟹x1x2=√2
The ratio of the distances the springs are compressed is:
x1x2=√2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE
2 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
Two discs A and B are mounted coaxially ona vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The loss of kinetic energy the above process is -
View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1 Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2 Both the discs rotate in the clockwise direction.
When disc B is brought in contact with disc A, they acquire a common angular velocity in time t. The average frictional torque on one disc by the other during this period is
View SolutionA disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is

View Solution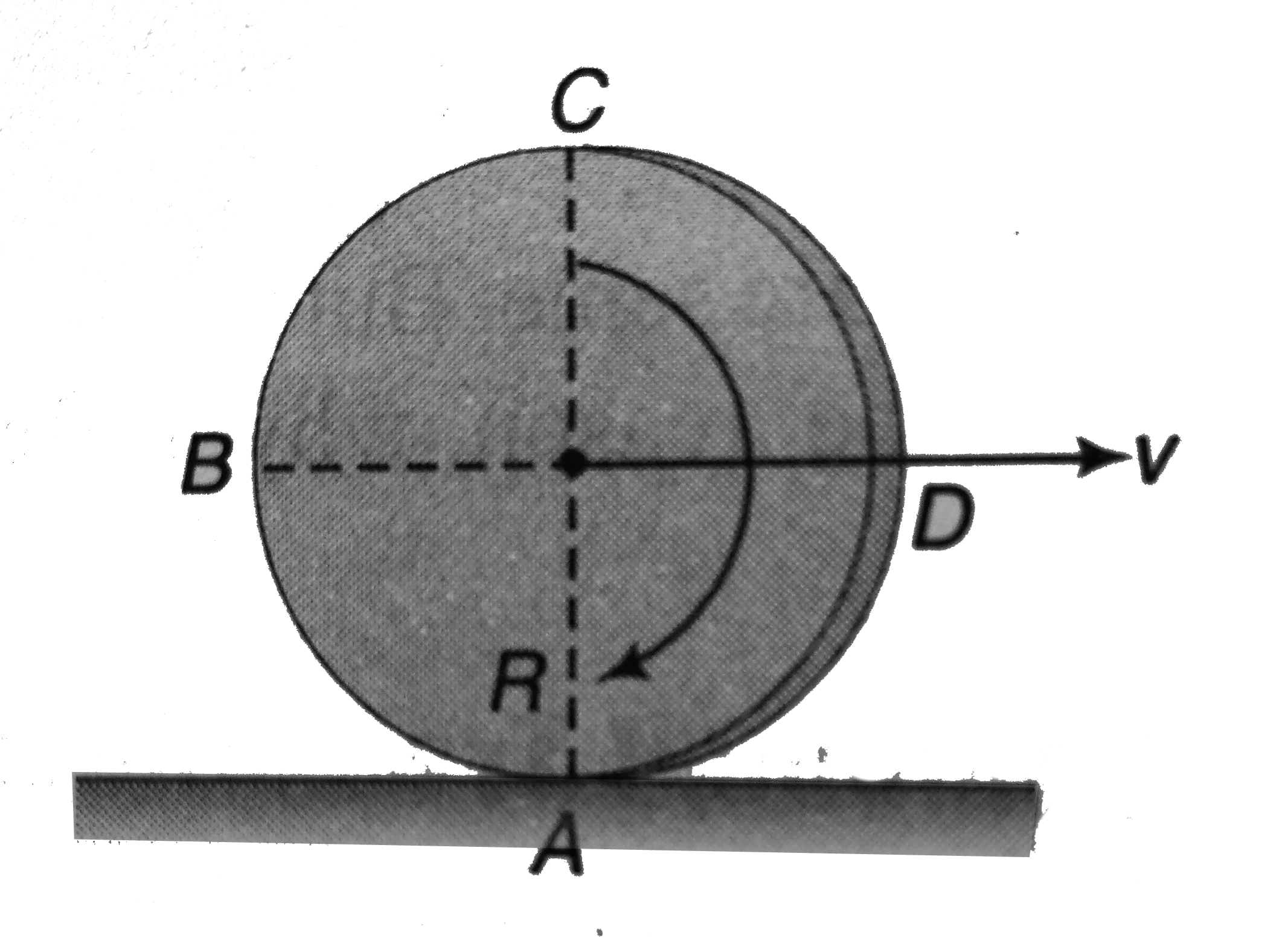
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View SolutionTwo discs are mounted on frictionless bearings on a common shaft. The first disc has rotational inertia / and is spinning with angular velocity ω. The second disc has rotational inertia 2/ and is spinning in opposite direction with angular velocity 3ω, as shown in figure. The two discs are slowly forced towards each other along the shaft until they couple and have a final common angular velocity of

View SolutionA circular disc is rotating about its own axis at an angular velocity ω. If P is exact midpoint of dise between axis and rim of disc then angular velocity of Pis
View SolutionA non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.

View SolutionTwo discs A and B have same mass and same thickness. If d1 and d2 are the densities of the materials of the discs A and B respectively, then the ratio of the moment of inertia of the discs A and B about their geometrical axis is
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View Solution
