A frog sits on the end pf a long boord of length L. the boord rests on a fricationless horizontal table. The frog wants os the minimum takes - off speed i.e relative to ground v that allows the frog yo do the trick? The board and the frog have equal masses.
The correct Answer is:2
To solve the problem of determining the minimum take-off speed of the frog relative to the ground, we can follow these steps:
Step 1: Understand the System
We have a frog sitting at one end of a long board of length L. The board is resting on a frictionless horizontal table, and both the frog and the board have equal masses.
Step 2: Apply Conservation of Momentum
Since there are no external horizontal forces acting on the system (frog + board), we can apply the principle of conservation of momentum. Let m be the mass of the frog (which is equal to the mass of the board).
When the frog jumps off the board with a velocity v relative to the ground, the board will move in the opposite direction. Let the velocity of the board after the frog jumps be u.
According to the conservation of momentum:
mv+mu=0
This simplifies to:
mv=−mu
From this, we can express u in terms of v:
u=−v1=−v
Step 3: Relate Distances Covered
The frog jumps a horizontal distance x while the board moves a distance L−x in the opposite direction. The time t taken for both the frog and the board to cover their respective distances can be expressed as:
t=xv(for the frog)
t=L−xu(for the board)
Since both events happen simultaneously, we can set these two equations equal:
xv=L−xu
Step 4: Substitute for u
Substituting u=−v1 into the equation gives:
xv=L−x−v
Cross-multiplying leads to:
x(−v)=v(L−x)
This simplifies to:
−xv=vL−vx
Rearranging gives:
2xv=vL
Thus, we find:
x=L2
Step 5: Use Kinematic Equations
Now, we can use the kinematic equations to relate the distance x to the velocity v. The horizontal distance covered by the frog can also be expressed as:
x=vcos(θ)t
And for the vertical motion:
x=v2sin(2θ)g
Setting these equal gives:
L2=v2sin(2θ)g
Step 6: Solve for v
Rearranging the equation yields:
v2=gL2sin(2θ)
To find the minimum value of v, we need to maximize sin(2θ). The maximum value of sin(2θ) is 1, which occurs when 2θ=90∘ or θ=45∘.
Thus, we have:
v2=gL2
Taking the square root gives:
v=√gL2
Step 7: Substitute g
Assuming g=10m/s2:
v=√10L2=√5L
Final Answer
The minimum take-off speed v that allows the frog to jump off the board is:
v=√5Lm/s
We have a frog sitting at one end of a long board of length L. The board is resting on a frictionless horizontal table, and both the frog and the board have equal masses.
Since there are no external horizontal forces acting on the system (frog + board), we can apply the principle of conservation of momentum. Let m be the mass of the frog (which is equal to the mass of the board).
mv+mu=0
This simplifies to:
mv=−mu
From this, we can express u in terms of v:
u=−v1=−v
The frog jumps a horizontal distance x while the board moves a distance L−x in the opposite direction. The time t taken for both the frog and the board to cover their respective distances can be expressed as:
t=xv(for the frog)
t=L−xu(for the board)
Since both events happen simultaneously, we can set these two equations equal:
xv=L−xu
Substituting u=−v1 into the equation gives:
xv=L−x−v
Cross-multiplying leads to:
x(−v)=v(L−x)
This simplifies to:
−xv=vL−vx
Rearranging gives:
2xv=vL
Thus, we find:
x=L2
Now, we can use the kinematic equations to relate the distance x to the velocity v. The horizontal distance covered by the frog can also be expressed as:
x=vcos(θ)t
And for the vertical motion:
x=v2sin(2θ)g
Setting these equal gives:
L2=v2sin(2θ)g
Rearranging the equation yields:
v2=gL2sin(2θ)
To find the minimum value of v, we need to maximize sin(2θ). The maximum value of sin(2θ) is 1, which occurs when 2θ=90∘ or θ=45∘.
v2=gL2
Taking the square root gives:
v=√gL2
Assuming g=10m/s2:
v=√10L2=√5L
The minimum take-off speed v that allows the frog to jump off the board is:
v=√5Lm/s
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - SCQ_TYPE
12 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Linked Comprehension
105 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A frog sits on the end of a long board of length L=5m. The board rests on a frictionless horizontal table. The frog wants to jump to the opposite end of the board. What is the minimum take-off speed (in m/s), i.e., relative to ground 'v' that allows the frog to do the trick? The board and the frog have equal masses.
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v/2 relative to the rod towards the end A. The spider takes negligible time in eating the insect. Also, let v=L/T, where T is a constant having value 4sec.The speed of the bar after the spider eats up the moth and moves towards A is
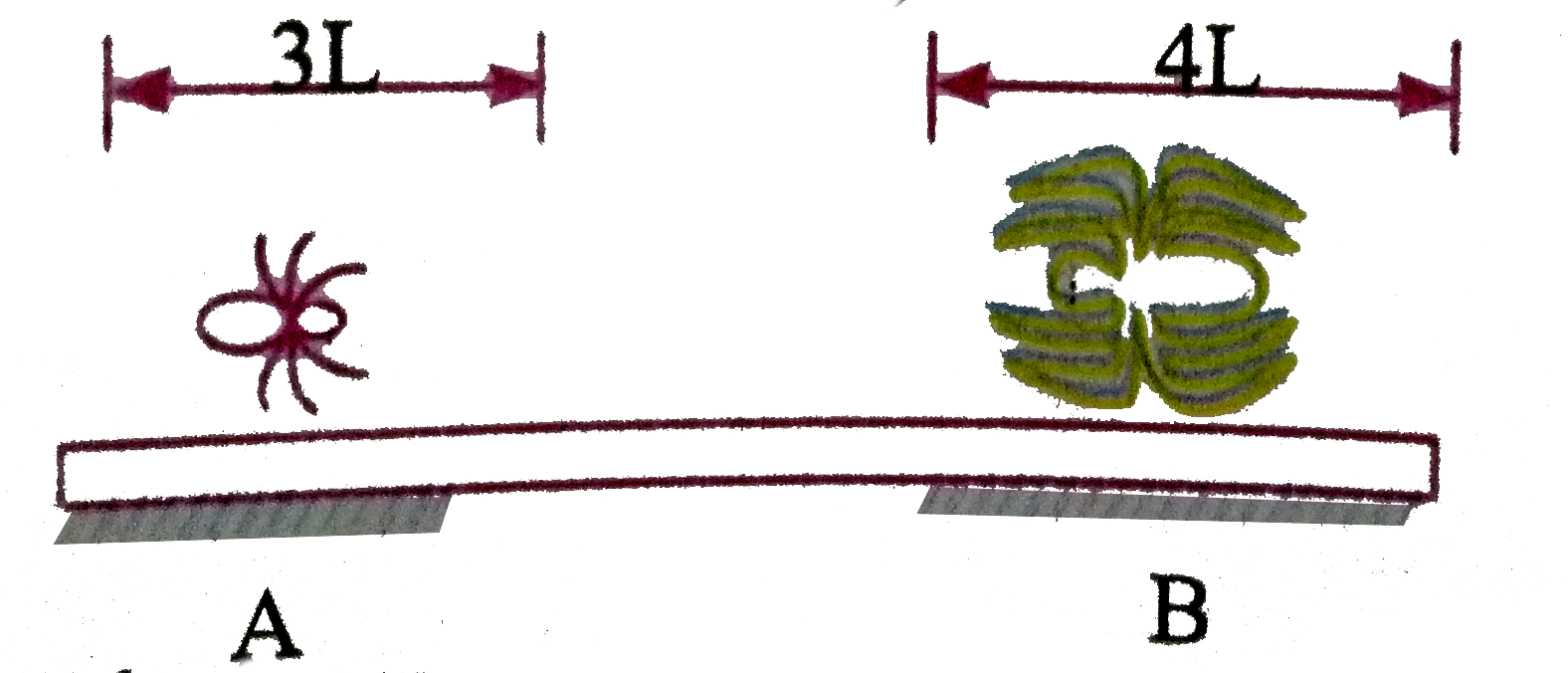
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
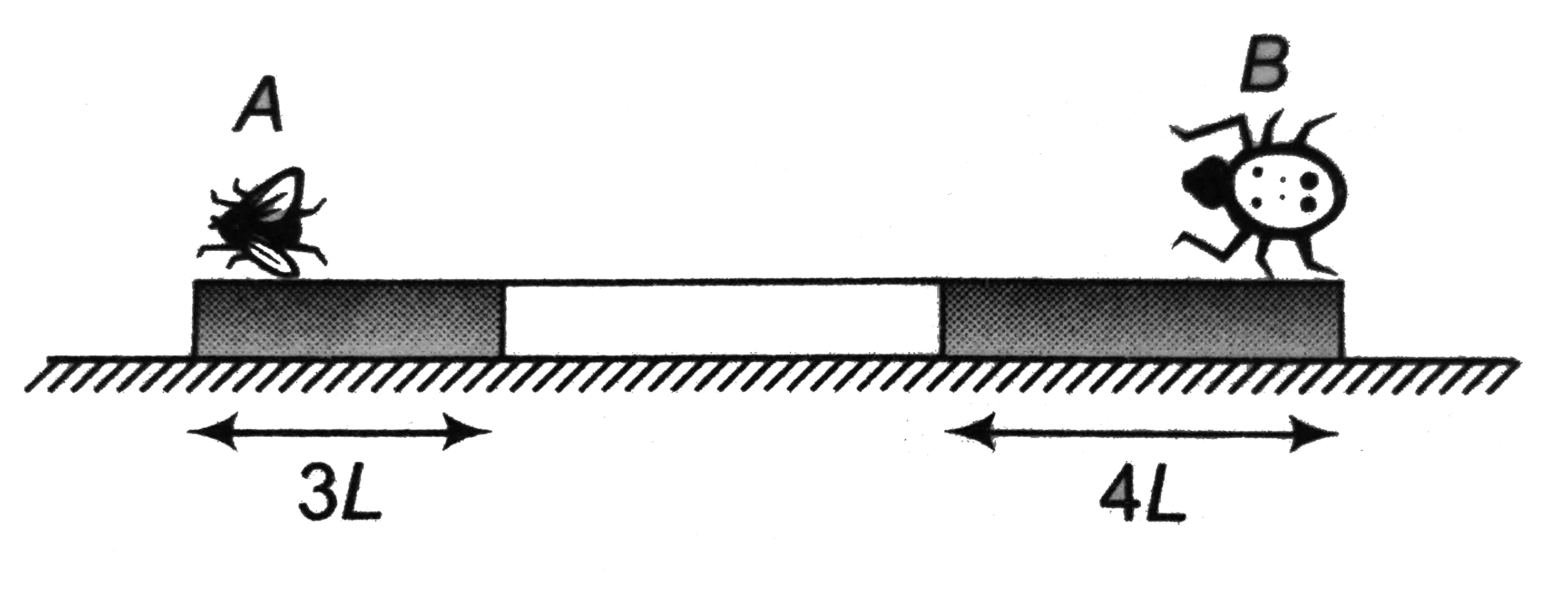
After starting from end B of the rod the spider reaches the end A at a time
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
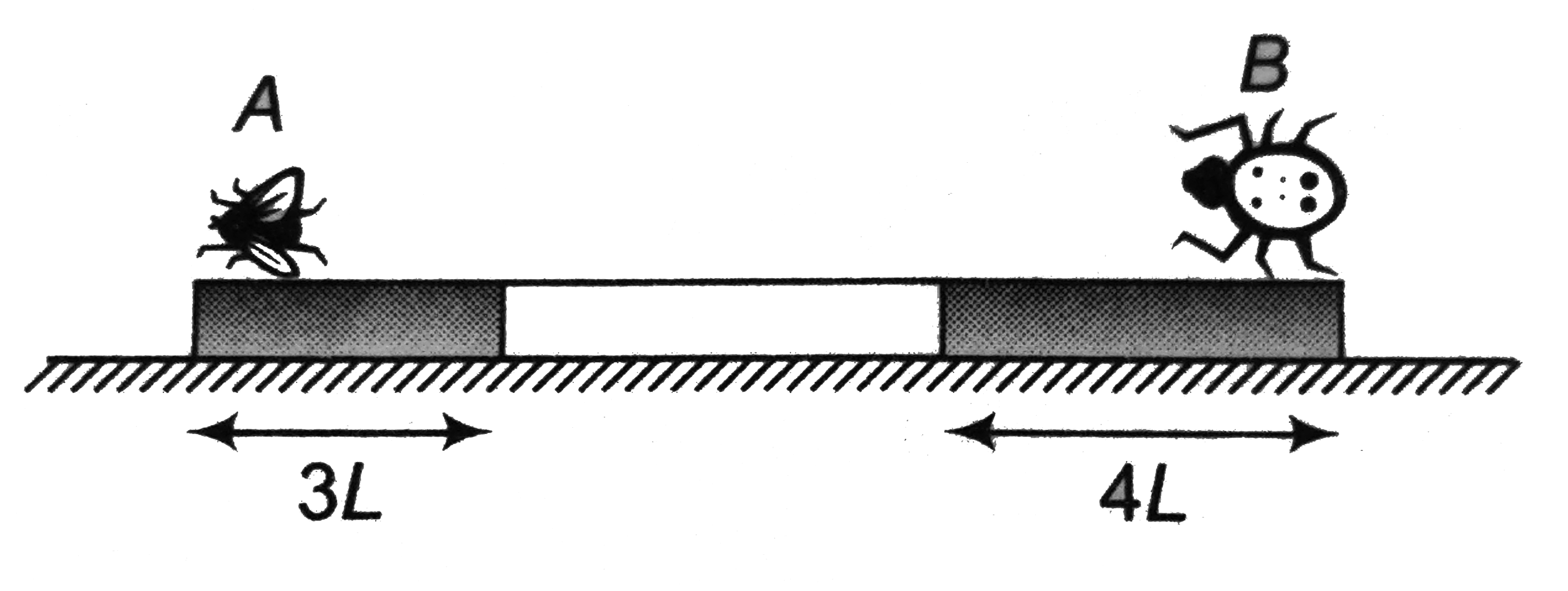
By what distance the centre of mass of the rod shifts during this time?
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with the moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. Also, let v=L/T, where T is a constant having value 4sec. The point P is at
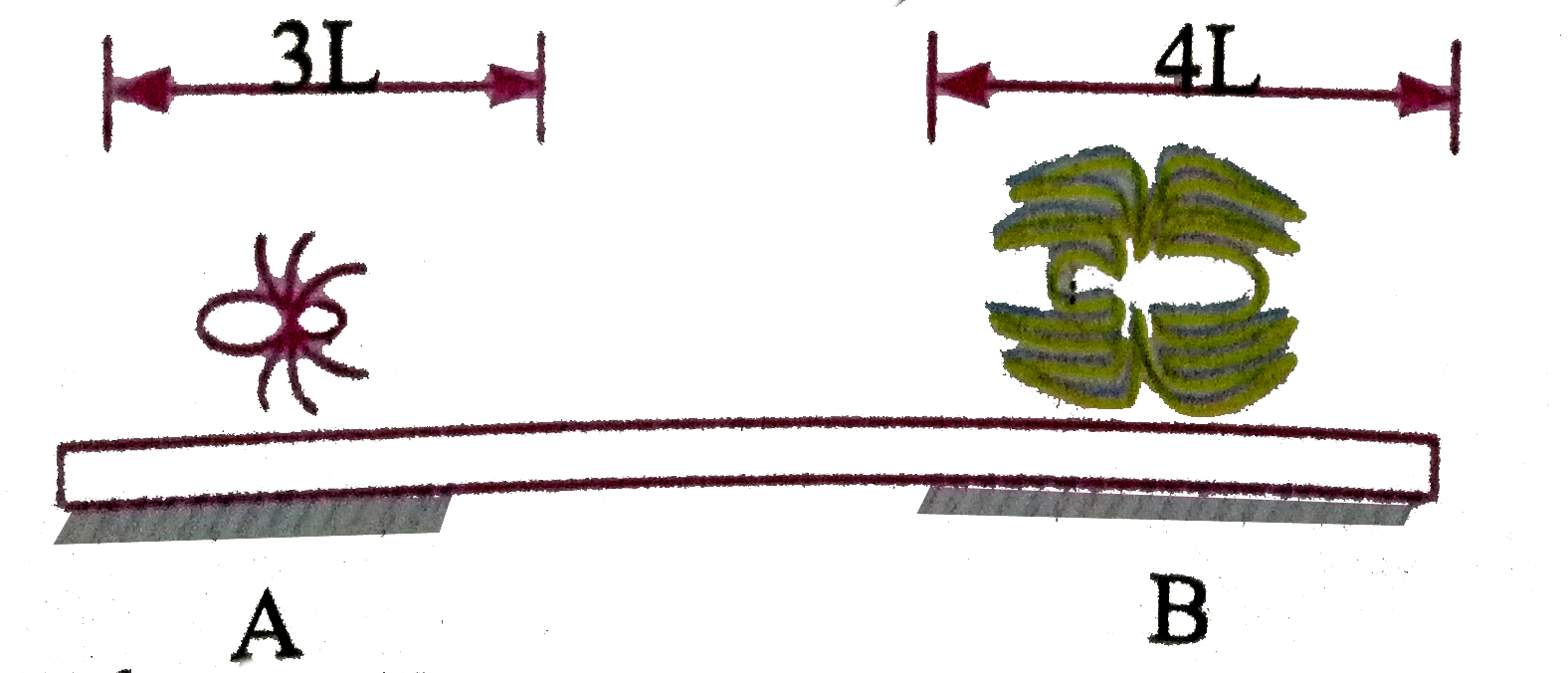
View Solution
