A uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
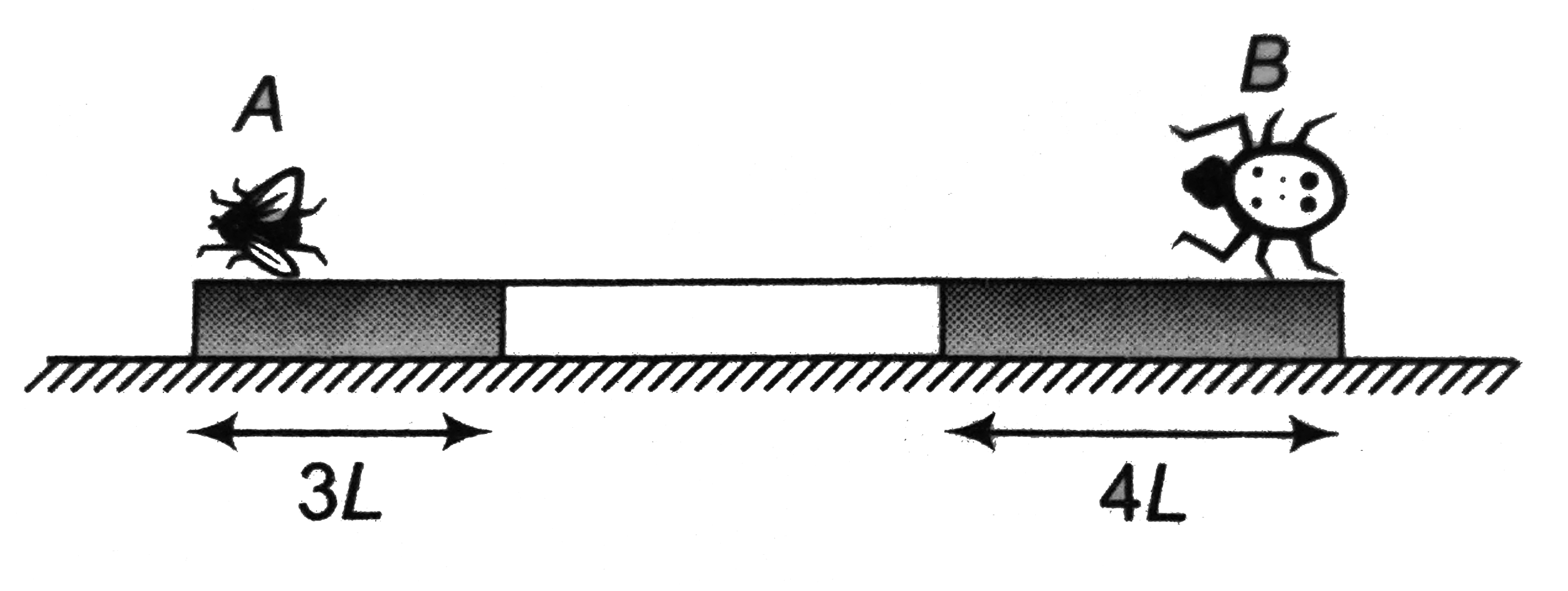
By what distance the centre of mass of the rod shifts during this time?
(a) 8L3
(b) 4L3
(c) L
(d) L3
The correct Answer is:A
Till t1, rod is stationary. For time t2 rod is moving with absolute speed u(=v/6)
∴ Displacement of rod =(v6)t2
=(v6)(16Lv)=8L3
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Comprehension Based
4 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
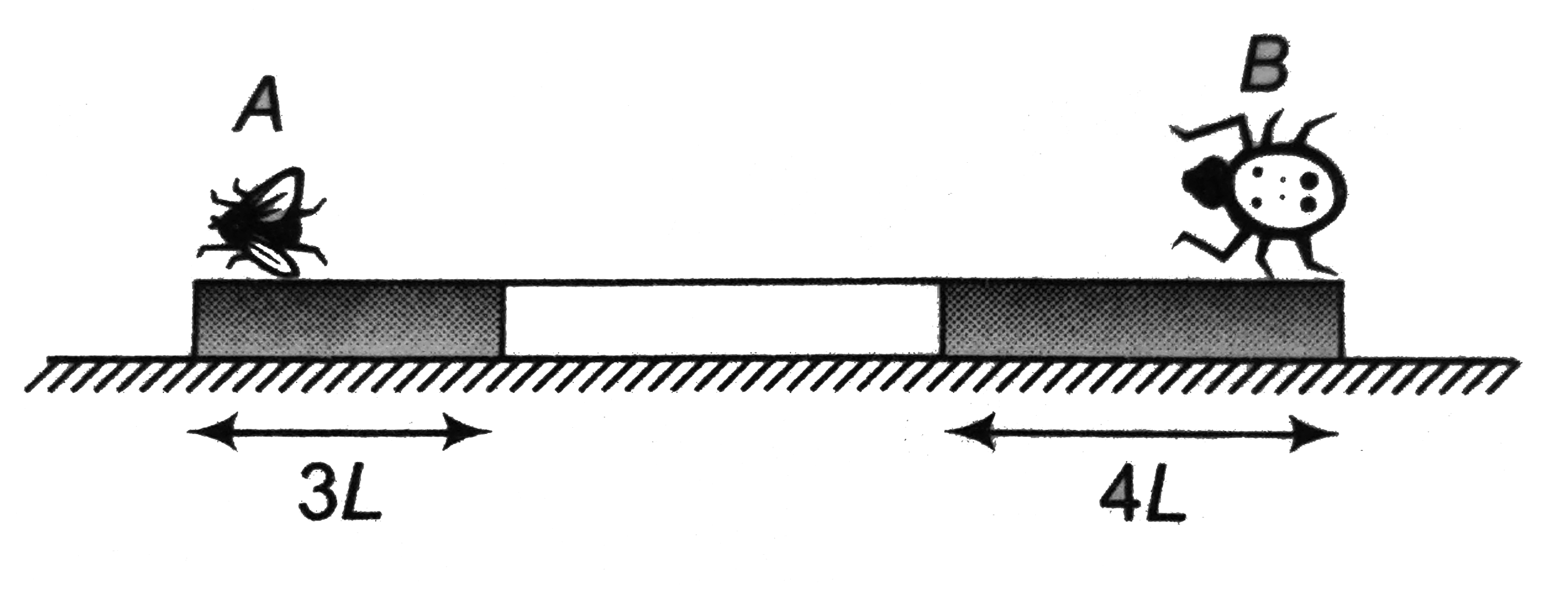
After starting from end B of the rod the spider reaches the end A at a time
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v/2 relative to the rod towards the end A. The spider takes negligible time in eating the insect. Also, let v=L/T, where T is a constant having value 4sec.The speed of the bar after the spider eats up the moth and moves towards A is
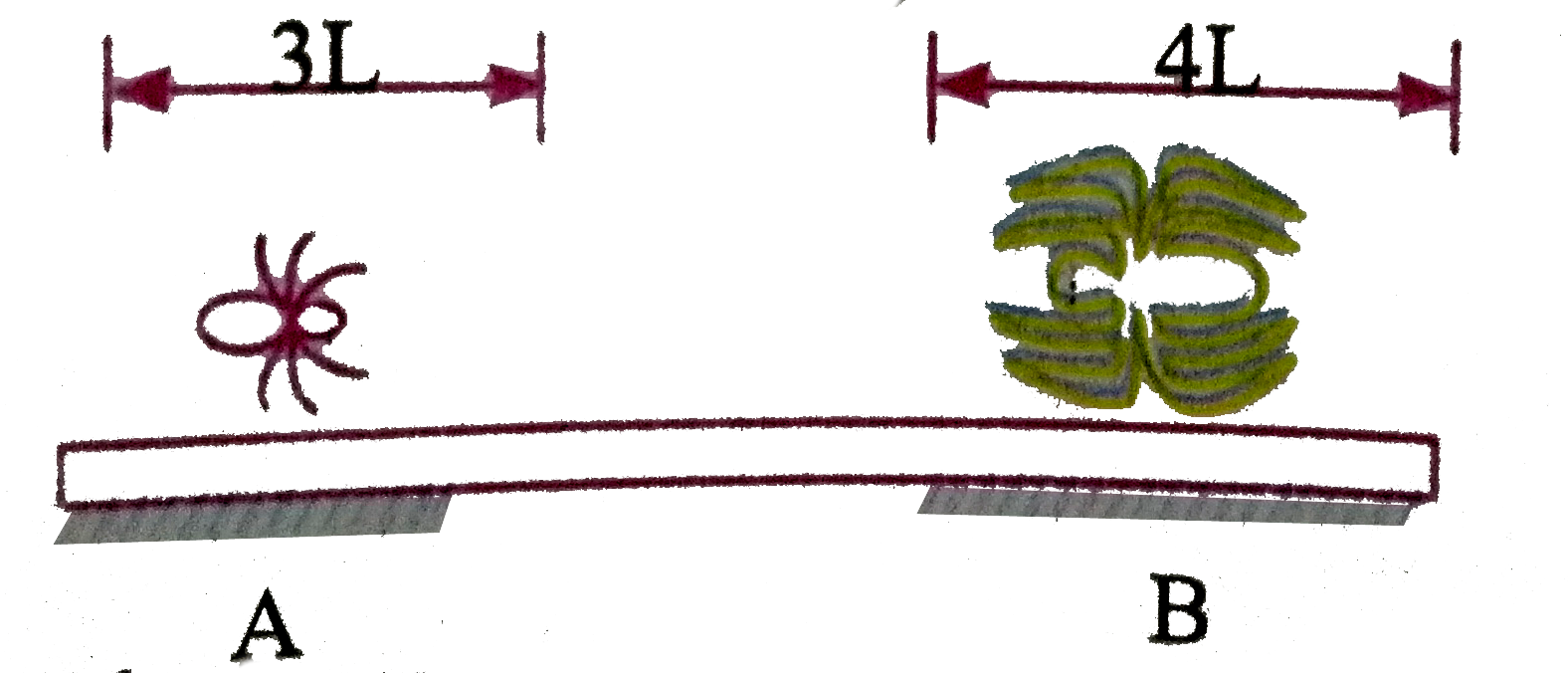
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with the moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. Also, let v=L/T, where T is a constant having value 4sec. The point P is at
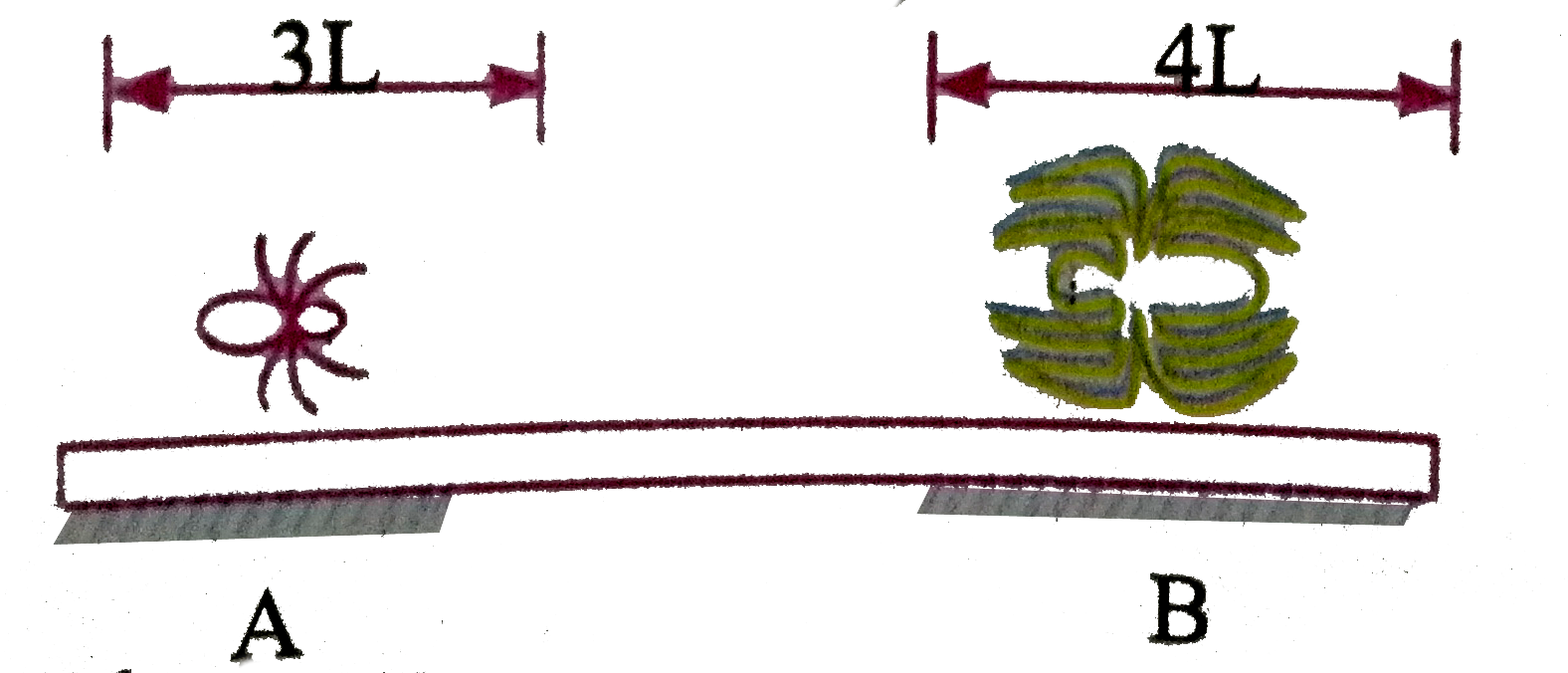
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of mass m and length L is kept on a horizontal table with L4 length on the table as shown in figure. As the string attached to the end B is cut, the angular acceleration of the rod about point C will be
_PHY_E05_242_Q01.png)
View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View SolutionA strip of wood of mass M and length l is placed on a smooth horizontal surface. An insect of mass m starts at one end of the strip and walks to the other end in time t, moving with a constant speed. The speed of the insect as seen from the ground is
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision.
View SolutionA horizontal rod of mass M and length L is tied to two verticle string symmetrically as shown in the figure. One of the strings at end Q is cut at t=0 and the rod starts rotating about the other and P then

View Solution
