A strip of wood of mass M and length l is placed on a smooth horizontal surface. An insect of mass m starts at one end of the strip and walks to the other end in time t, moving with a constant speed. The speed of the insect as seen from the ground is
lt(MM+m)
lt(mM+m)
lt(Mm)
lt(mM)
The correct Answer is:A
To solve the problem, we need to find the speed of the insect as seen from the ground. Let's break it down step by step.
Step 1: Understand the system
We have a strip of wood with mass M and length l on a smooth horizontal surface. An insect with mass m walks from one end of the strip to the other in time t with a constant speed.
Step 2: Define variables
Let:
- u = speed of the insect as seen from the ground
- v = speed of the strip of wood as it moves in the opposite direction to the insect
Step 3: Initial momentum
Initially, the system (insect + strip) is at rest, so the total initial momentum is zero:
0=M⋅0+m⋅0
Step 4: Final momentum
As the insect walks to the other end of the strip, the wood will move in the opposite direction to conserve momentum. The final momentum of the system can be expressed as:
m⋅u+M⋅(−v)=0
This simplifies to:
m⋅u=M⋅v(1)
Step 5: Relate speeds in the ground frame
In the ground frame, the speed of the insect as it walks on the strip is:
v′=u+v
where v′ is the speed of the insect relative to the ground.
Step 6: Distance traveled by the insect
The insect travels the length l of the strip in time t. Therefore, we can express the relationship as:
v′⋅t=l(2)
Step 7: Substitute v′ from (2) into (1)
From equation (2), we have:
(u+v)⋅t=l
This can be rearranged to:
u+v=lt(3)
Step 8: Solve for v
From equation (1), we can express v in terms of u:
v=mMu(4)
Substituting equation (4) into equation (3):
u+mMu=lt
Factoring out u:
u(1+mM)=lt
Thus,
u=lt⋅MM+m(5)
Step 9: Final expression for speed
The speed of the insect as seen from the ground is:
u=lt⋅MM+m
Summary
The speed of the insect as seen from the ground is given by:
u=lt⋅MM+m
We have a strip of wood with mass M and length l on a smooth horizontal surface. An insect with mass m walks from one end of the strip to the other in time t with a constant speed.
Let:
- u = speed of the insect as seen from the ground
- v = speed of the strip of wood as it moves in the opposite direction to the insect
Initially, the system (insect + strip) is at rest, so the total initial momentum is zero:
0=M⋅0+m⋅0
As the insect walks to the other end of the strip, the wood will move in the opposite direction to conserve momentum. The final momentum of the system can be expressed as:
m⋅u+M⋅(−v)=0
This simplifies to:
m⋅u=M⋅v(1)
In the ground frame, the speed of the insect as it walks on the strip is:
v′=u+v
where v′ is the speed of the insect relative to the ground.
The insect travels the length l of the strip in time t. Therefore, we can express the relationship as:
v′⋅t=l(2)
From equation (2), we have:
(u+v)⋅t=l
This can be rearranged to:
u+v=lt(3)
From equation (1), we can express v in terms of u:
v=mMu(4)
Substituting equation (4) into equation (3):
u+mMu=lt
Factoring out u:
u(1+mM)=lt
Thus,
u=lt⋅MM+m(5)
The speed of the insect as seen from the ground is:
u=lt⋅MM+m
The speed of the insect as seen from the ground is given by:
u=lt⋅MM+m
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Multiple Correct
Explore 25 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Subjective
Explore 23 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
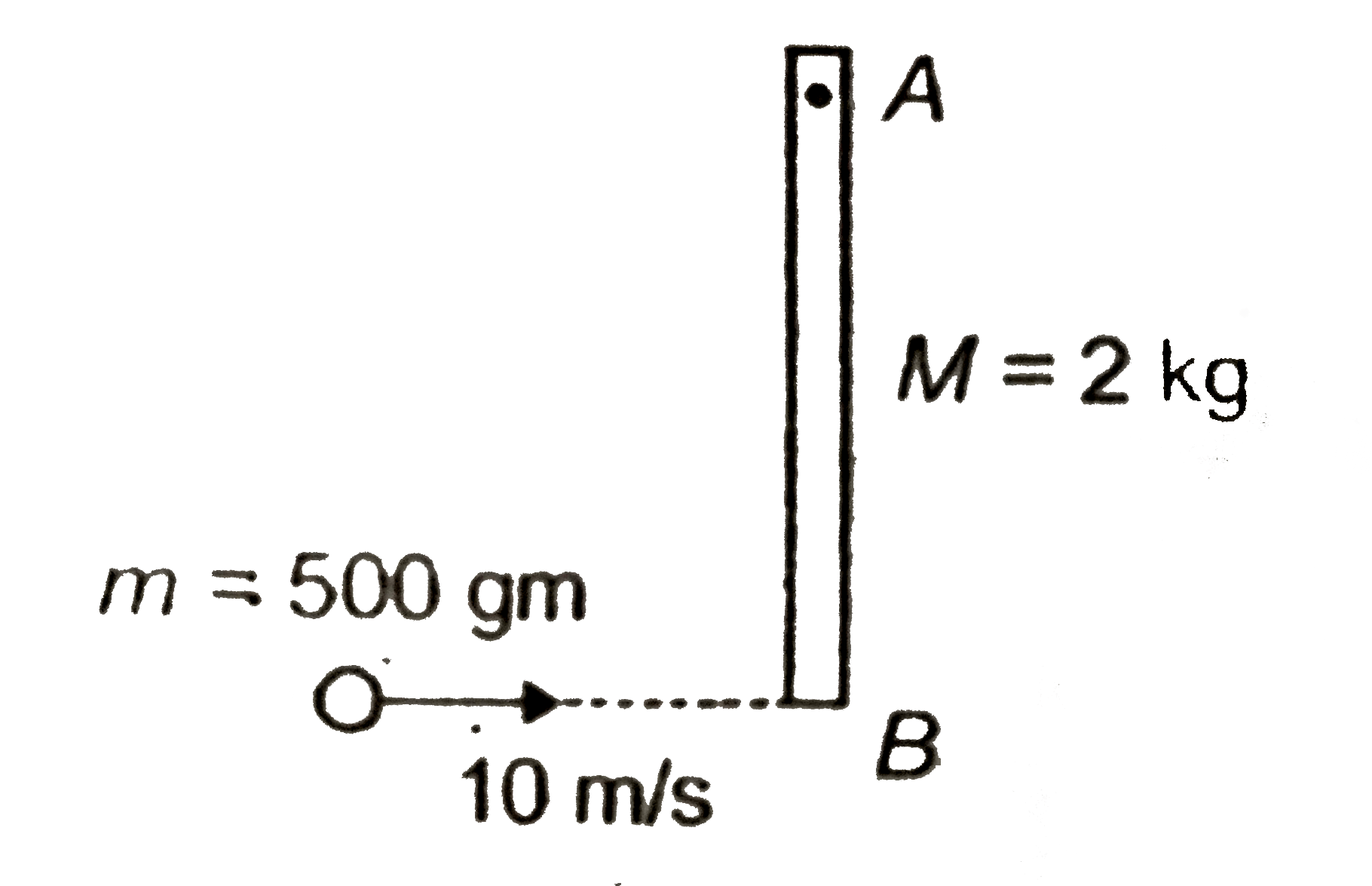
A rod of mass 2kg and length 1m is pivoted at one end A and kept on a smooth surface. A particle of mass 500gmstrikestheotherendB of the rod and sticks to the rod. If particle was moving with the speed of 10m/s, what is the angular speed of the rod after collision ?
View SolutionA rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
View SolutionA wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
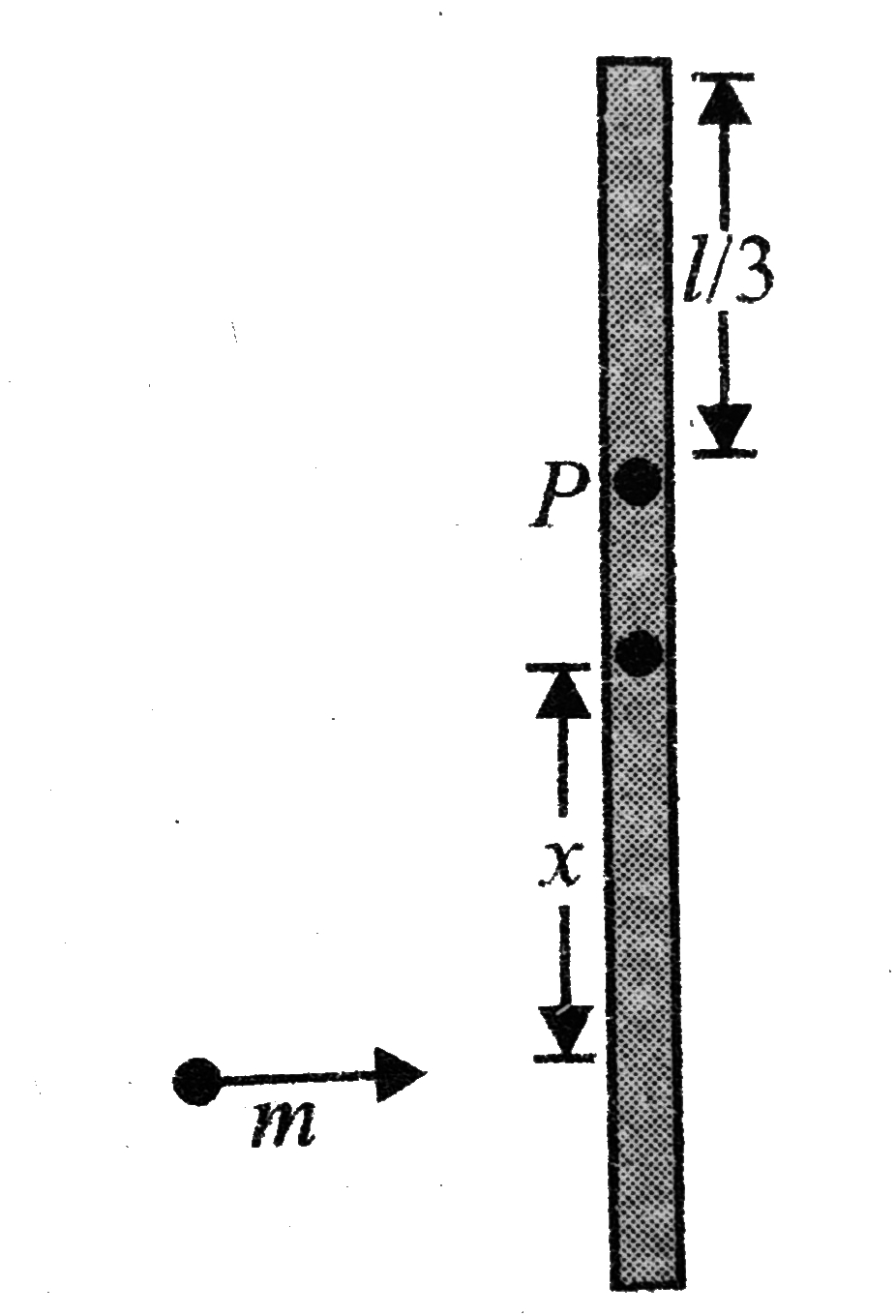
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
View SolutionA rod of mass M and length L is placed on a smooth horizontal surface. It is hinged at one end so that it can rotate freely in a horizontal circle about this end. There exists a uniform magnetic field →B perpendicular, into the horizontal surface everywhere. The strength of magnetic field starts varying as B=B0t.
(i) Find the torque acting on the rod about its hinged end.
(ii) Find the reaction produced at hinge at t = 0.
(A charge Q is distributed uniformaly on the rod)
View Solution

