Question

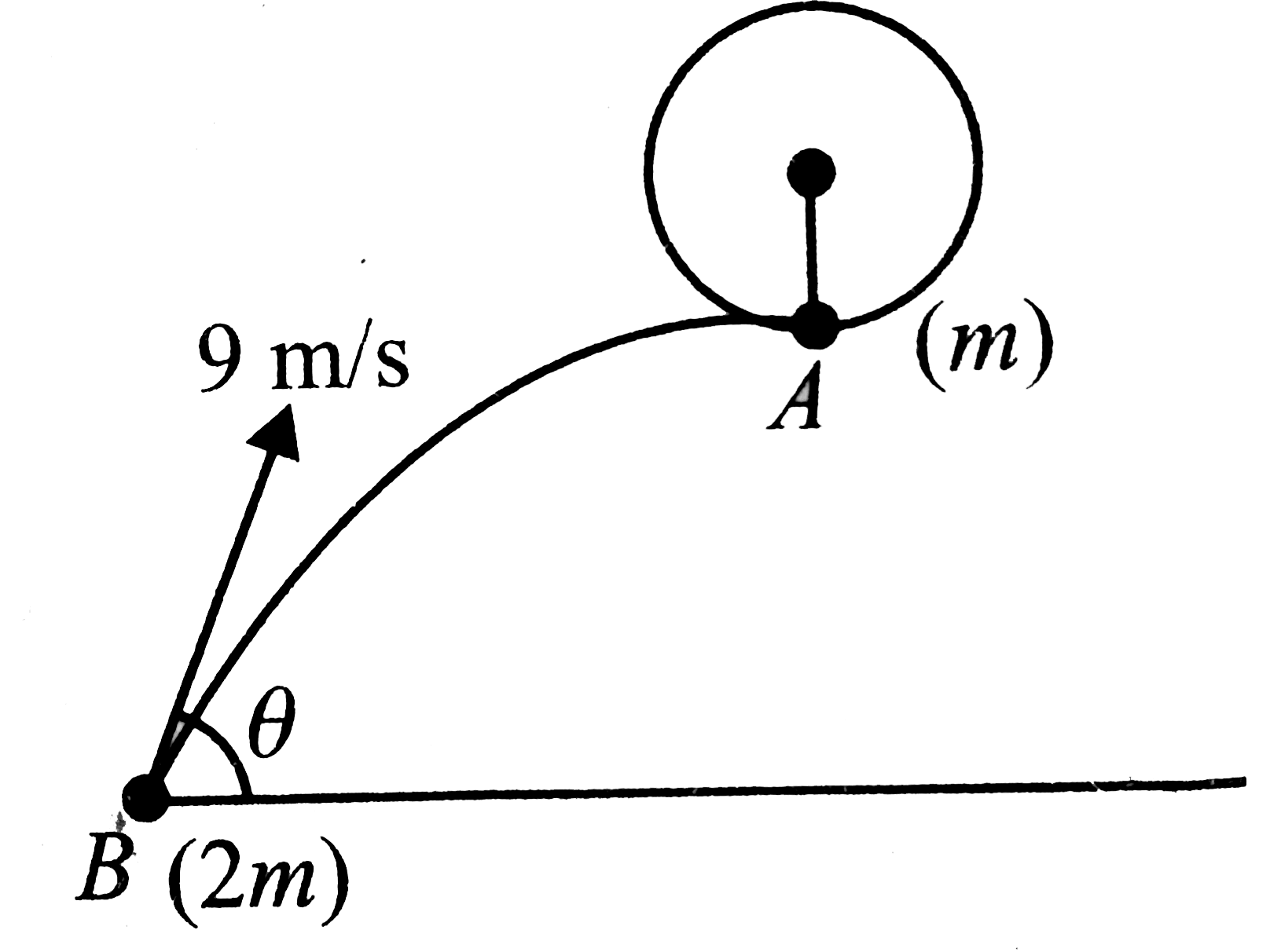
A ball A of mass $m$ is suspended by a thread of length $r=1.2m$. Another ball $B$ of mass $2m$ is projected from the ground with velocity it $u=9m/s$ such that at the highest point of its trajectory it collides head-on elastically with ball $A$. It is observed that during subsequent motion, tension in the thread at the highest point is equal to $mg$.

The angle of projection ($\theta$) of ball $B$ is

Options

A. a. `30^(@)`
B. `60^(@)`
C. `45^(@)`
D. `75^(@)`

Answer

B

Explanation

Let velocity of ball `A` at highest point be `v` then first considering its `FBD` at this point

`mg+ T=(mv^(2))/r`
where` T=mg`
`implies v^(2)=2rg`
`implies v=sqrt(2rg)=2sqrt(6)m//s`
If the velocity of ball `A` just after the collisin is `v_(1)` then according to law of conservation of energy its `KE` at `A=(KE+PE)` at highest point
`1/2mv_(1)^(2)=1/2mv^(2)+mg(2r)`
`v_(1)=sqrt(6rg)` or `v_(1)=6sqrt(2)m//s`
If angle of project of ball `B` is `theta`, then horizontal component of its velocity will be `9 costheta` and it remains constant.

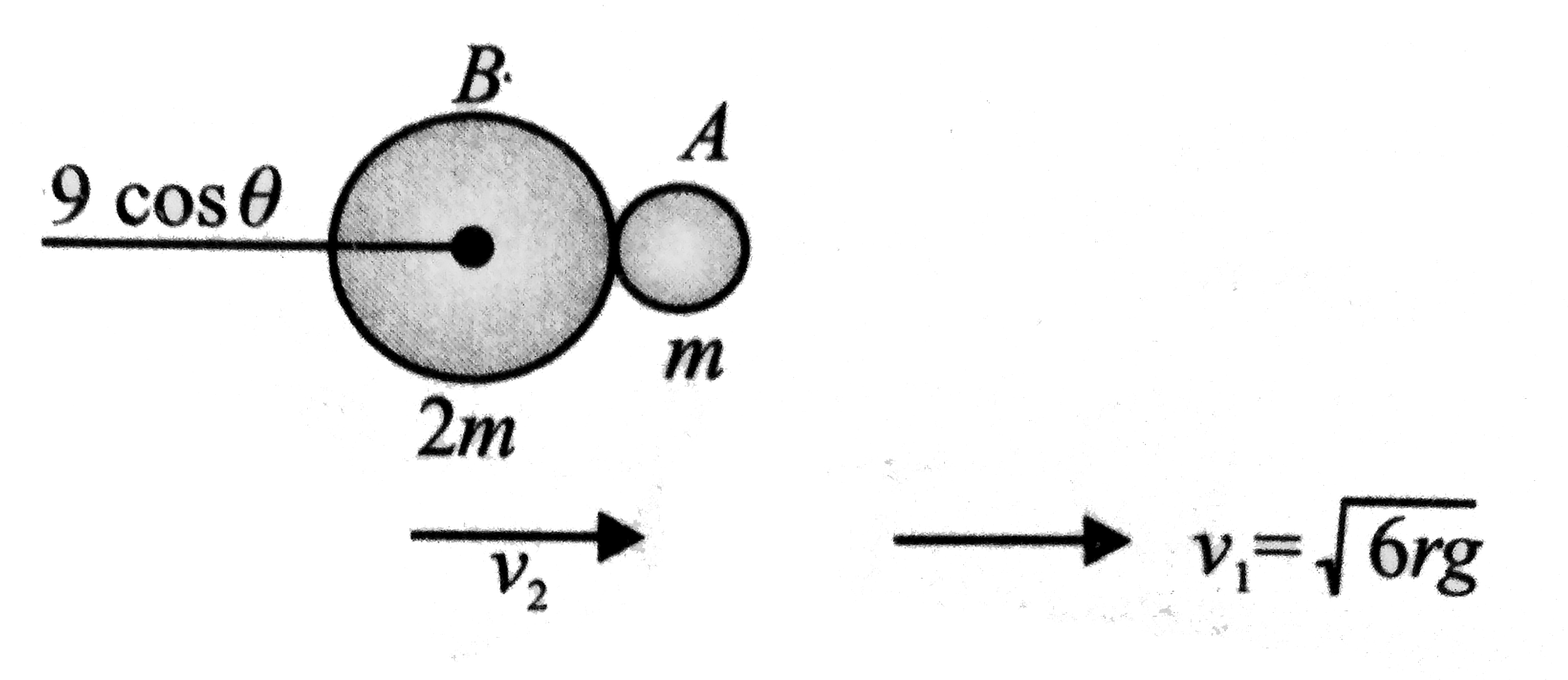
Now considering collision of balls `B` and `A`, let velocities of balls `A` and `B`, just after the collision, be `v_(1)` and `v_(2)` respectively as shown in figure.
Then according to the law of conservation of momentum
`mv_(1)+2mv_(2)=2m(9costheta)` ...........i
Since collision is elastic, therefore `e=1`
`(v_(1)-v_(2))/(9costheta)=1` or `v_(1)-v_(2)=9costheta` ........ii
Solving eqn i and ii we get
`costheta=1/(sqrt(2))` or `theta=45^(@)`
`v_(2)=3/(sqrt(2))ms^(-1)`
height of initial position of ball `A` (lowest position) is equal to maximum height ascened by the ball `B`. It is equal to
`H=((9sintheta)^(2))/(2g)=81/40m`
Height of point of suspension from the ground is
`H=r=129/40m`