A string with one end fixed on a rigid wall, passing over a fixed frictionless pulley at a distance of 2m from the wall, has a point mass M of 2kg attached to it at a distance of 1m from the wall. A mass m of 0.5kg is attached to the free end. The system is initially held at rest so that the stirng is horizontal between wall and pulley and vertical beyond the pulley as shown in figure.

What will be the speed with which point mass M will hit the wall when the system is released? (g=10ms−2)
2(√5+√56)m/s
2(√5−√56)m/s
5(√5−√56)m/s
5(√5+√56)m/s
The correct Answer is:C
When M strikes the wall, vertically downward component of its displacement from initital position is 1m and its distance from pulley B is
C'B=√12+22=√5m
When its initial distance from the pulley was CB=1m. It means vertically upward displacement of mass m is (√5−1)m.
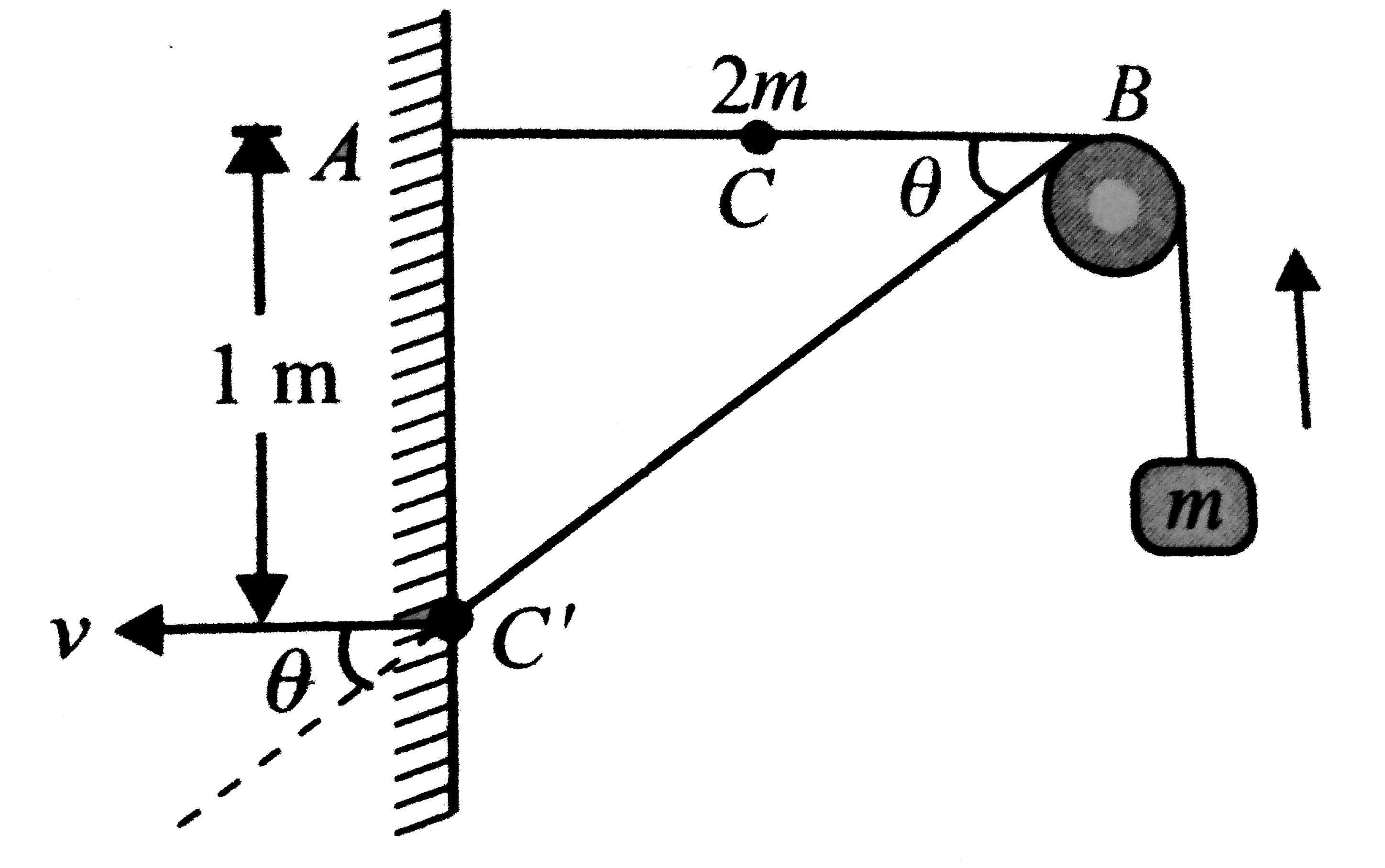
Let M strike the wall velocity v. Since the string between the two blocks always remains taut, therefore at any instant speed of m is equal to that component of velocity of M which which is along the string C'B. Hence , velocity of m when M strikes the wall is vcosθ, where
cosθ=2√5
∴vMvm=vvcosθ=√52
According to law of energy, loss of potential energy of M=increase in PE of m+KE of M+KE of m
Mg×1=mg(√5−1)+12Mv2+12m(vcosθ)2
v=5√5−√56m/s
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Integer
Explore 16 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Fill In The Blanks
Explore 2 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:Assertion - Reasoning
Explore 2 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICS ENGLISHChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
Two masses m1=5kg and m2=4.8kg tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when left free to move?
View SolutionA 3m along ladder weighing 20kg leans on a frictionless wall. Its feet rest on the floor 1m from the wall. Find the rection forces of the wall and the floor.
View Solution
Knowledge Check
A 3m along ladder weighing 20kg leans on a frictionless wall. Its feet rest on the floor 1m from the wall. Find the rection forces of the wall and the floor.
A25√2 N, 203 NB50√2 N, 230 NC203 N, 25√2 ND230N,50√2 N
A mass m rests on a horizontal table. It is attached to a light inextensible string which passes over a smooth pulley and carries a mass m at the other end. If the mass m is raised vertically through a distance h and is then dropped, what is the speed with which the mass 2m begins to rise?

View SolutionA body of mass 20 kg is resting on a table. A light string is attached to it and passed over a smooth pulley at the edge of the table and a mass 3kg is attached at the free end. What is the acceleration of the system of the coefficient of kinetic friction between the mass and the table is 0.04 ? What is the tension in the string ?
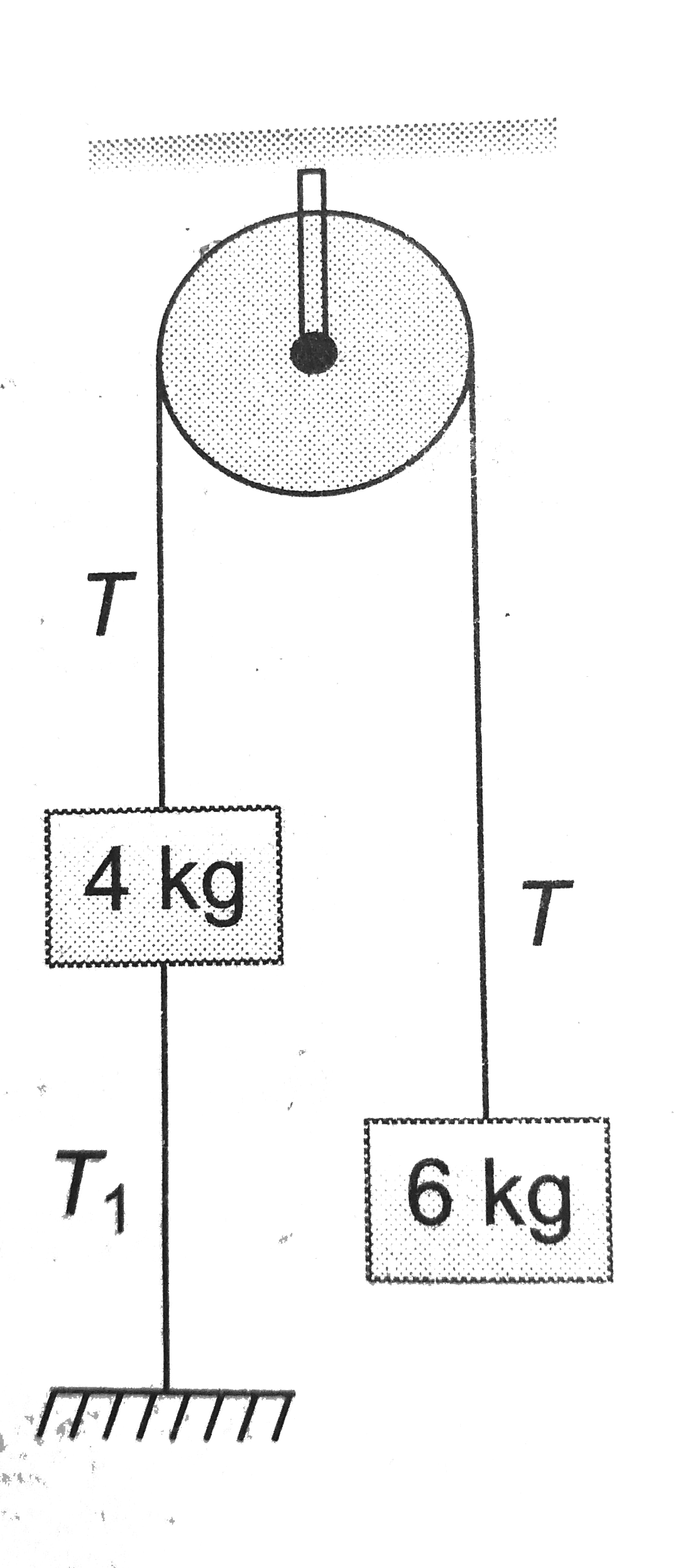
View SolutionTwo bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
View SolutionA ring of mass m=1kg can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of L=0.7m from the rod as shown in figure.
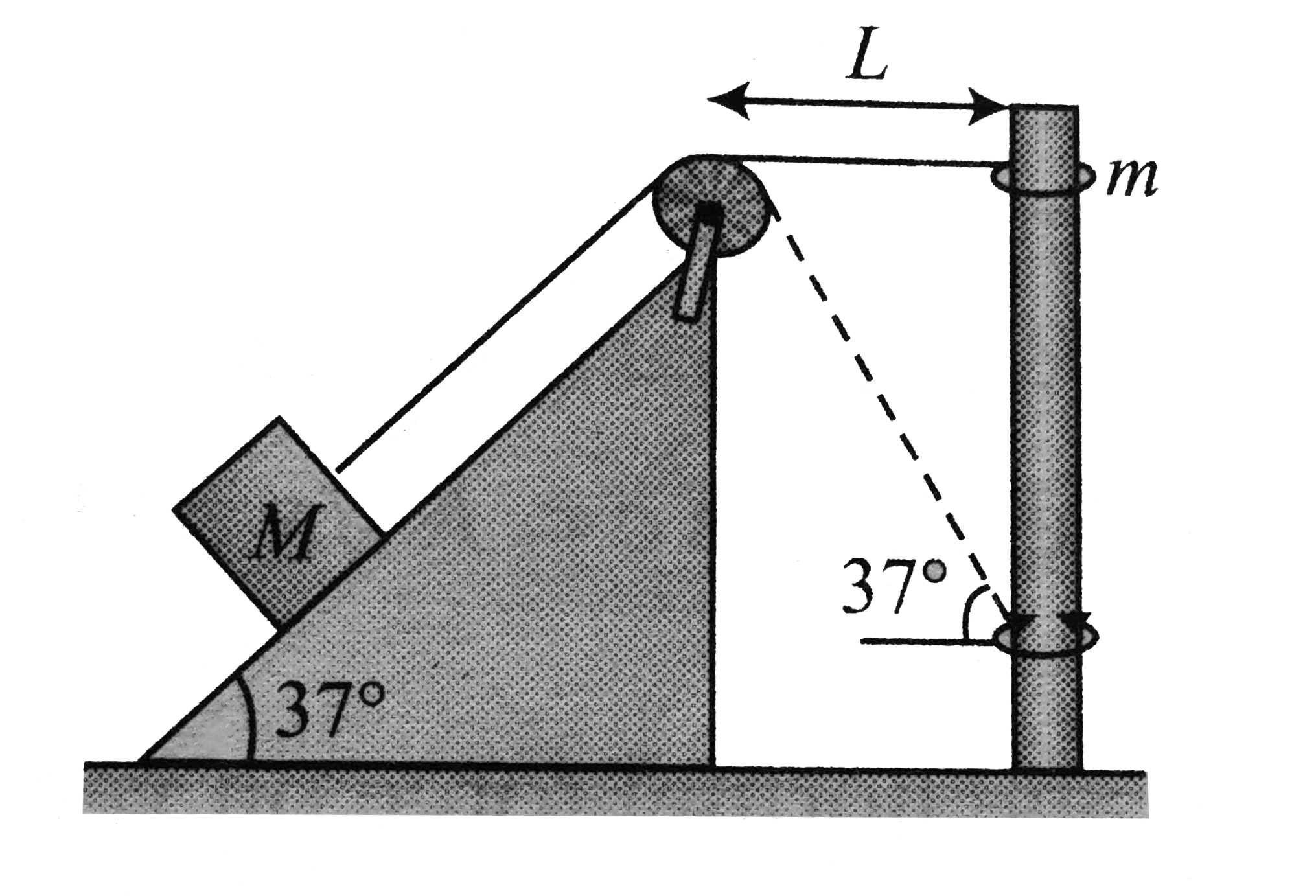
At the other end of the string mass M=5kg is attached, lying over a smooth fixed inclined plane of inclination angle 37∘. The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle (α=37∘) with the horizontal. [sin37∘=0.6]
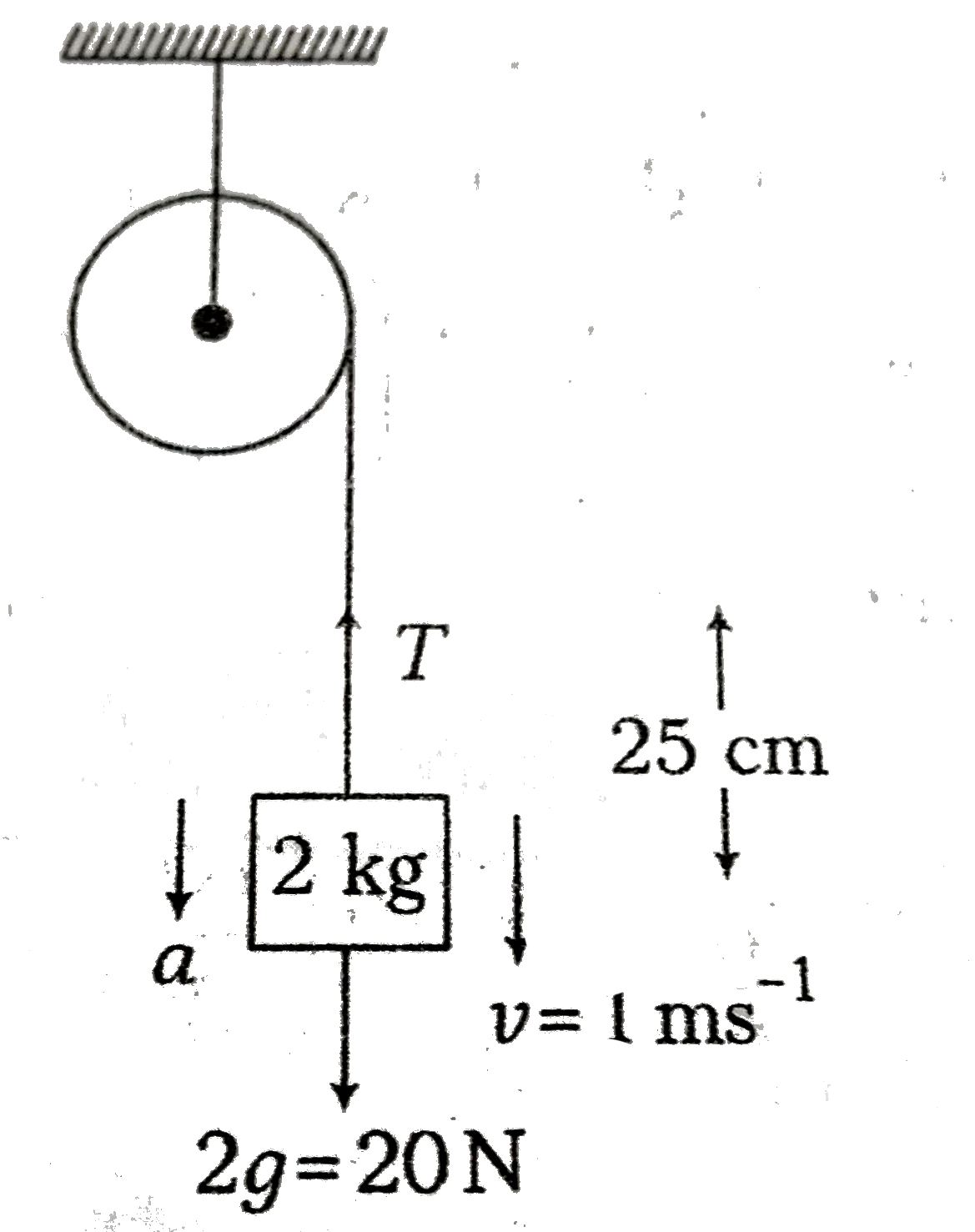
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)
View SolutionA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?

View SolutionA mass of 0.2 kg is attached to the lower end of a massless spring of force constant 200Nm the other end of which is fixed to a rigid support. Study the following statements.
View Solution
