According to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass $M$ is placed on a smooth horizontal surface. light identical springs, each of stiffness $K$ , are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is $3 l$ . A block of mass $m$ is placed on the plank and pressed against one of the springs so that it is compressed to $l$ . To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.

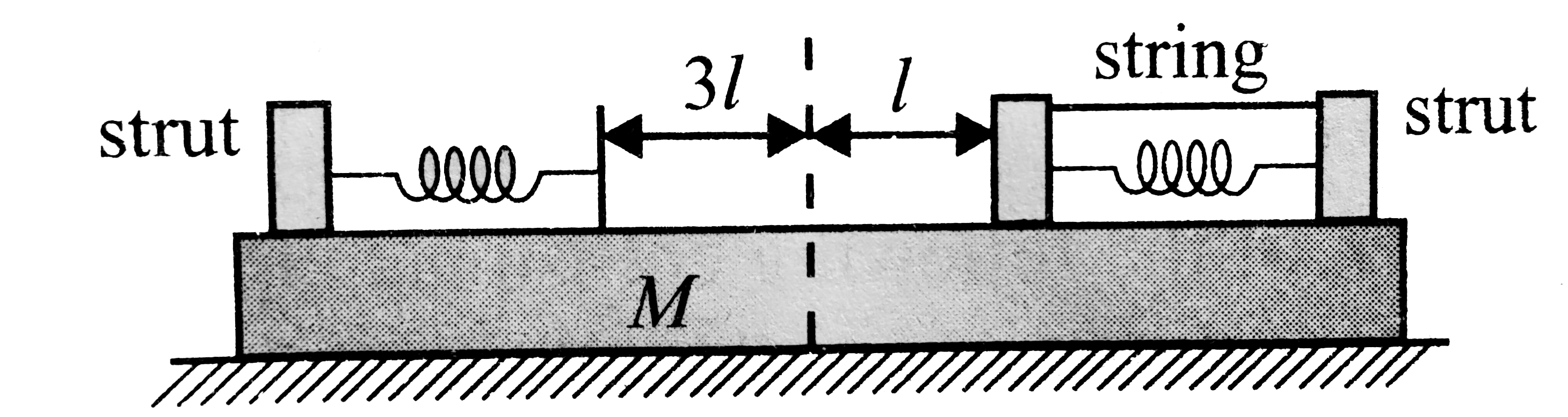
The maximum kinetic energy of the block $m$ is

A

$\frac{K m l^{2}}{2 M (M + m)}$

B

$\frac{K m l^{2}}{M (M + m)}$

C

$\frac{K M l^{2}}{2 (M + m)}$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$v_{m} = \frac{M}{m} \sqrt{\frac{K m}{M (M + M)}} l = \sqrt{\frac{K M}{m (M = m)}} l$
$K E = \frac{1}{2} m v_{m}^{2} = \frac{K M l^{2}}{2 (M + m)}$

Updated on:21/07/2023

|

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-CENTRE OF MASS-Linked Comprehension

Home
Ask Doubt
Profile