Consider the following two statements:
A. linear momentum of the system remains constant.
B. Centre of mass of the system remains at rest
A implies B and B implies A
A does not imply B and B does not imply A.
A implies B but B does not imply A
B implies A but A does not imply B
The correct Answer is:D
If CM is at rest, it definitetlyy means momentum of hte system is constant. But momentum of the system is constant, it does not mean center of mass is at rest.
Topper's Solved these Questions
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Assertion and reason
Explore 21 Videos
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Match the coloumns
Explore 9 Videos
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Check points
Explore 50 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEY ENGLISHChapter:CALORIMETRY AND HEAT TRANSFERExercise:Medical entrance s gallery
Explore 38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
Similar Questions
Consider the following two statements:
A. Kinear momentum of the system remains constant.
B. Centre of mass of the system remains at rest
View SolutionCalculate centre of mass of the system
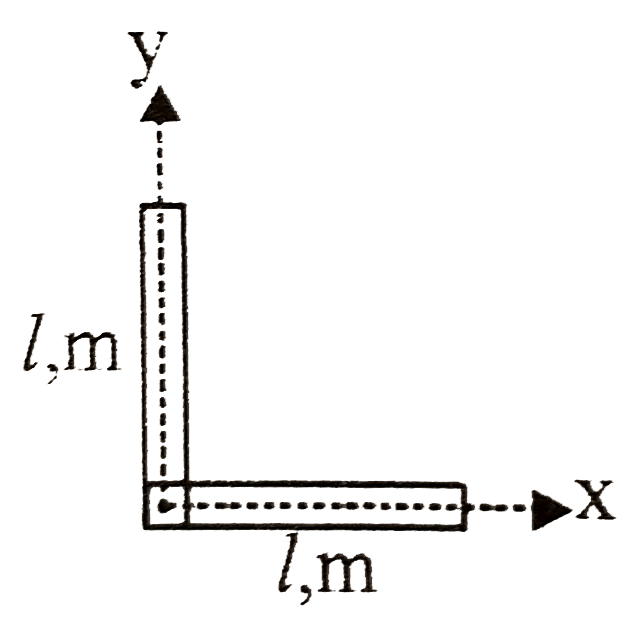
View SolutionConsider the following two statements:
A. Linear momentum of a system of partcles is zero.
B. Kinetic energ of a system of particles is zero.
View SolutionConsider the following two statements:
A. Linear momentum of a system of particles is zero.
B. Kinetic energy of a system of particles is zero.
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.
View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
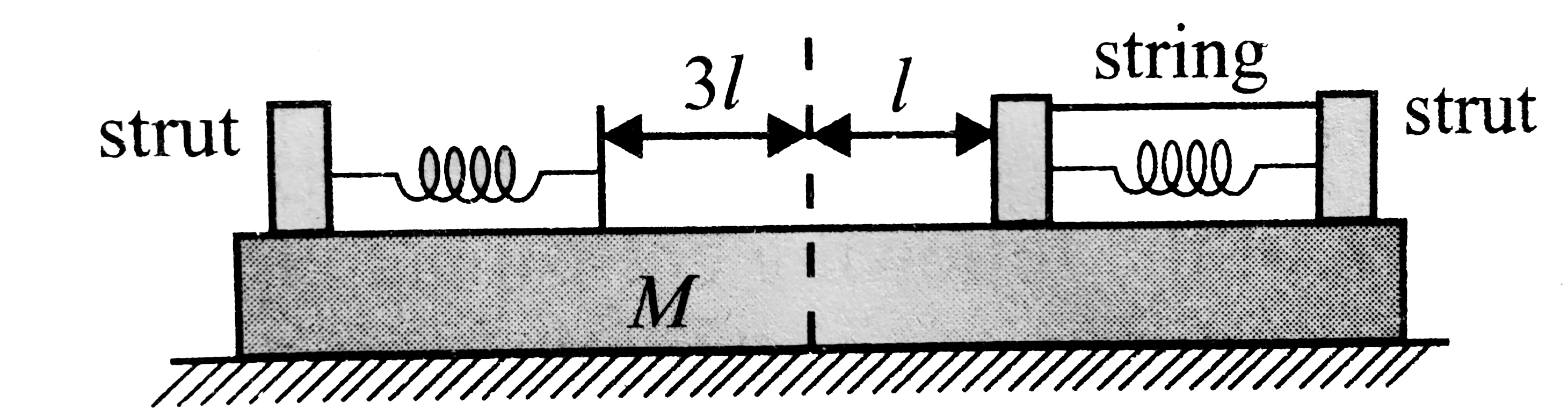
The maximum kinetic energy of the block m is
View SolutionThe momentum of a system with respect to centre of mass
View SolutionConsider the following two statements:
A The linear momentum of a particle is independent of the frame of reference.
B. The kinetic energy of a particle is independent of the frame of reference
View SolutionIf temperature of the system remains constant during the course of change, the change is
View SolutionThe magnitude of acceleration of centre of mass of the system is

View Solution