We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. Find time taken by him to across the river.
(3d/5)1/3
(6d/5)1/3
(6d/5)1/2
(2d/3)1/3
The correct Answer is:B
b. a=5t⇒dvydt=5t⇒vy=5t22
⇒dydt=52t2⇒y=56t3
Putting y=d,we≥td=52t3⇒t=(6d5)1/3.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Integer Type
Explore 17 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Fill in the blanks
Explore 4 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS KINEMATICSExercise:Multiple Correct Answer Type
Explore 26 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICS ENGLISHChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single correct anwer type
Explore 14 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
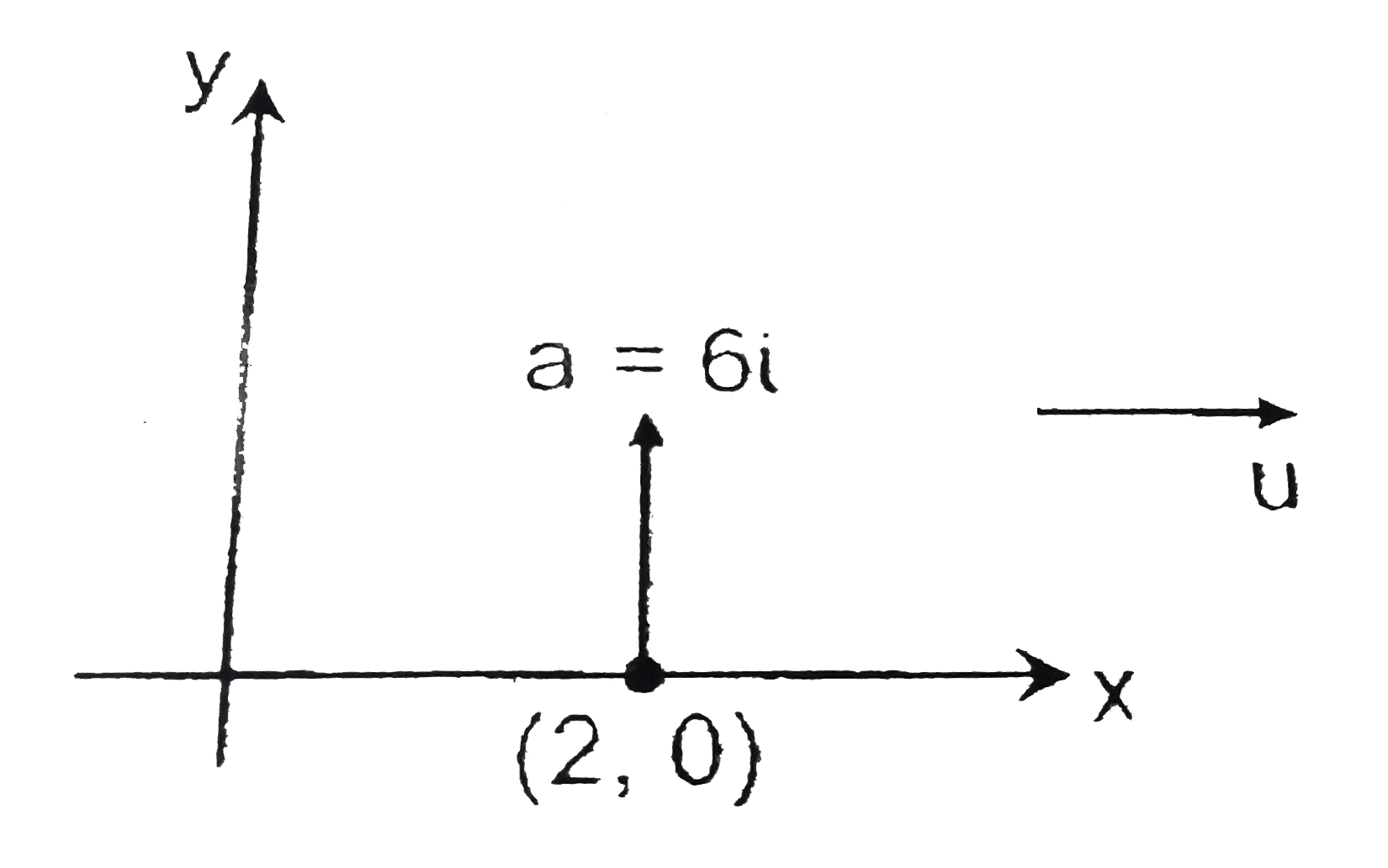
A boat starting from rest aims perpendicular to the river with an acceleration of a=6t
(where t= time) the boat starts from (2,0) of the coordinate system. Find equation of trajectory. Given velocity of river =u.
View SolutionVelocity of the river with respect to ground is given by v0. Width of the river is d. A swimmer swims (with respect to water) perpendicular to the current with acceleration a=2t (where t is time) starting from rest from the origin O at t=0. The equation of trajectory of the path followed by the swimmer is

View SolutionA boat takes 4 hr upstream and 2 hr down the stream for covering the same distance. The ratio of velocity of boat to the water in river is
View SolutionThe width of a river is 2√3 km. A boat is rowed in direction perpendicular to the banks of river. If the drift of the boat due to flow is 2 km, the displacement of the boat is
View SolutionA boat crosses a river with a velocity of 8kmh. If the resulting velocity of boat is 10kmh then the velocity of river water is
View SolutionTwo particles A and B moving in a plane have velocities as shown in figure .Relative velocity of A w.r.t B
View SolutionA boat stems in a river with velocity 2ˆi+ˆj with respecitve to the ground. The river water flows with a velocity −3ˆi−4ˆj with respect to the ground. What is the relative velocity of boat w.r.t river water ?
View SolutionA boat moves in still water with a velocity which is k times less than the river flow velocity. Find the angle to the stream direction at which the boat should be rowed to minimize drifting.
View SolutionA boat moves in still water with a velocity which is k times less than the river flow velocity. Find the angle to the stream direction at which the boat should be rowed to minimize drifting.
View SolutionAn object has velocity →v1 w.r.t. ground. An observer moving with constant velocity →v0 w.r.t. ground measures the velocity of the object as →v2. The magnitudes of three velocities are related by
View Solution