A boat moves in still water with a velocity which is k times less than the river flow velocity. Find the angle to the stream direction at which the boat should be rowed to minimize drifting.
The correct Answer is:cos−1(1/k)
Let the flow velocity of river be u and the velocity of boat in still water be v. Thus,
v=uK

Also, let the boat move at an angle θ with the direction of stream.
Now the velocity of boat in the river is the vector resultant of the velocity of boat and flow velocity of river, which can be writtenas
→vB=(u−vcosα)ˆi+(usinα)ˆj
=(u+vcosθ)ˆi+(usinθ)ˆj
Hence, the time taken to cross the river =dusinθ
(d= width of the river)
Thus, the drift s=(u+vcosθ)⋅d
or s=d(cosecθ+vucotθ)
or dsdthη=d(cosecθcotθ−vμcosec2θ)=0
or vucosec2θ=cosecθcotθ
or cosθ=1korθ=cos−1(1k)
Topper's Solved these Questions
- INTRODUCTION TO VECTORS BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - SINGLE CORRECT ANSWER TYPE
40 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - MULTIPLE CORRECT ANSWER TYPE
13 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - CONCEPT APPLICATION EXERCISE 1.2
7 Videos
- INTEGRALSBOOK - CENGAGE ENGLISHCHAPTER - INTEGRALSEXERCISE - All Questions
764 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Archives (Numerical Value type)
2 Videos
Similar Questions
A boat moves relative to water with a velocity v which is n times less than the river flow velocity u. At what angle to the stream direction must the boat move to minimize drifting ?
View SolutionA boat moves relative to water with a velocity v which is n times less than the river flow velocity u. At what angle to the stream direction must the boat move to minimize drifting ?
View SolutionA boat moves relative to water with a velocity which is 'n' times the river flow
a) If n<1 boat can not cross the river
b) If n = 1 boat can not cross the river without drifting
c) If n>1 boat can cross the river along shortest path
d) Boat can cross the river what ever is the value of n excluding zero value
View SolutionA man can swim in still water at 4m/s river is flowing at 2m/s. the angle with downstream at which he should swim to cross the river minimum drift is
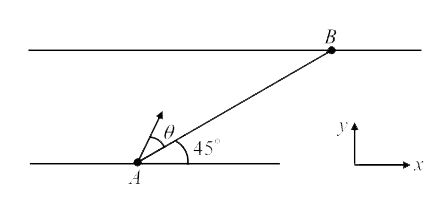
View SolutionA swimmer wants to directly reach the point B starting from A. The river is flowing along x-axis. If the velocity of the swimmer is √23 times the velocity of the river, find the angle θ from the line AB at which his swimming effort should be directed.
View SolutionThe force of resistance encountered by water on a motor boat of mass m going in still water with velocity v is proportional to the velocity v. At t=0 when its velocity is v0, then engine shuts off. Find an expression for the position of motor boat at time t and also the distance travelled by the boat before it comes to rest. Take the proportionality constant as k>0.
View SolutionA boat crosses a river with a velocity of 8kmh. If the resulting velocity of boat is 10kmh then the velocity of river water is
View SolutionA boat stems in a river with velocity 2ˆi+ˆj with respecitve to the ground. The river water flows with a velocity −3ˆi−4ˆj with respect to the ground. What is the relative velocity of boat w.r.t river water ?
View SolutionA ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.
View SolutionThe river 500 m wide is flowing with a current of 4kph. A boat starts from one bank of the river wishes to cross the river at right angle to stream direction. Boatman can row the boat at 8 kph. In which direction he should row the boat. What time he ''ll take to cross the river ?
View Solution
