Two identical blocks A and B, each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k with the spring at its natural length. A third identical block C (mass m) movimng with a speed v along the line joining A and B collides with A, the maximum compression in the spring is
(a) The KE of the AB system at maximum compression of the spring is zero.
(b) The KE of the AB system at maximum compression of the spring is .
(c) The maximum compression of the spring is .
(d) The maximum compression of the spring is
The correct Answer is:B, D
Initially, there will be collision between C and A which is elastic.
So by conservation of momentum, we have
(i)
And as in elastic collision, KE after collision is same as before collision, hence
i.e.,
Subtracting Eq. (ii) from the square of Eq. (i), we have
So, either or
corresponds to no interaction between A and C, so the only physically possible solution is , which is the light of Eq. (i) gives , i.e., after collision C stops and A starts moving with velocity v. Now A will move and compress the spring which in turn accelerates B and retards A and finally both A and B will move with same velocity (say V). In this situation, compression of the spring will be maximum.
As external force is zero, momentum of the system is conserved, i.e.,
By conservation of mechanical energy,
or
i.e., or
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (assertion-reasoning)
Explore 1 Video
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (linked Comprehension)
Explore 2 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (sinble Correct )
Explore 19 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
Two blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then

View SolutionTwo bodies A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a light spring of stiffness k.
A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. If lo be the natural length of the spring then find the minimum separation between the blocks.

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionTwo blocks A and B of mass 2m and m respectively are connected to a massless spring of force constant K as shown in figure A and B are moving on the horizontal frcitionless surface with velocity v to right with underformed spring. If B collides with C elastically, then maximum compression of the spring will be
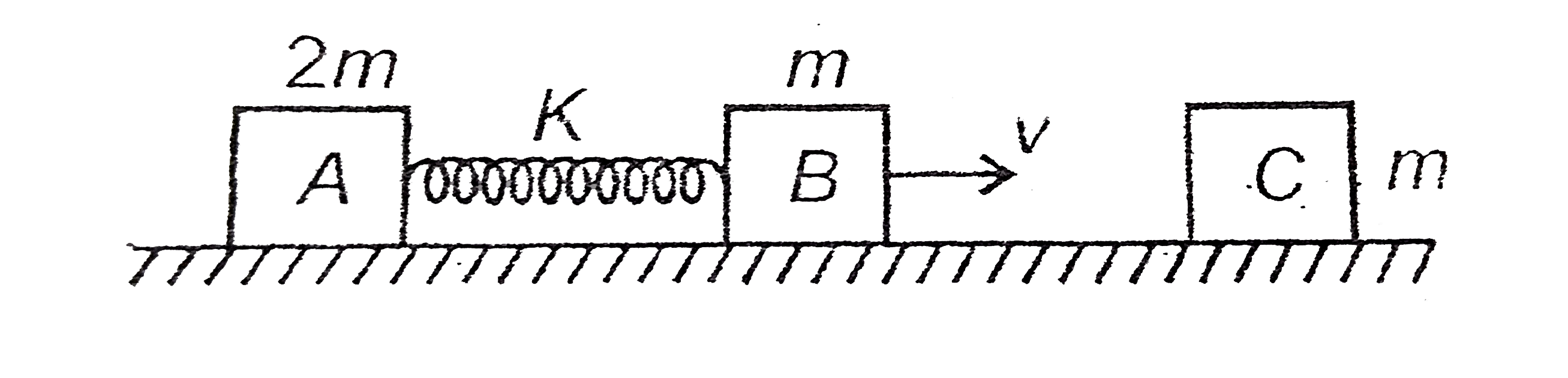
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionTwo blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity v0 along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
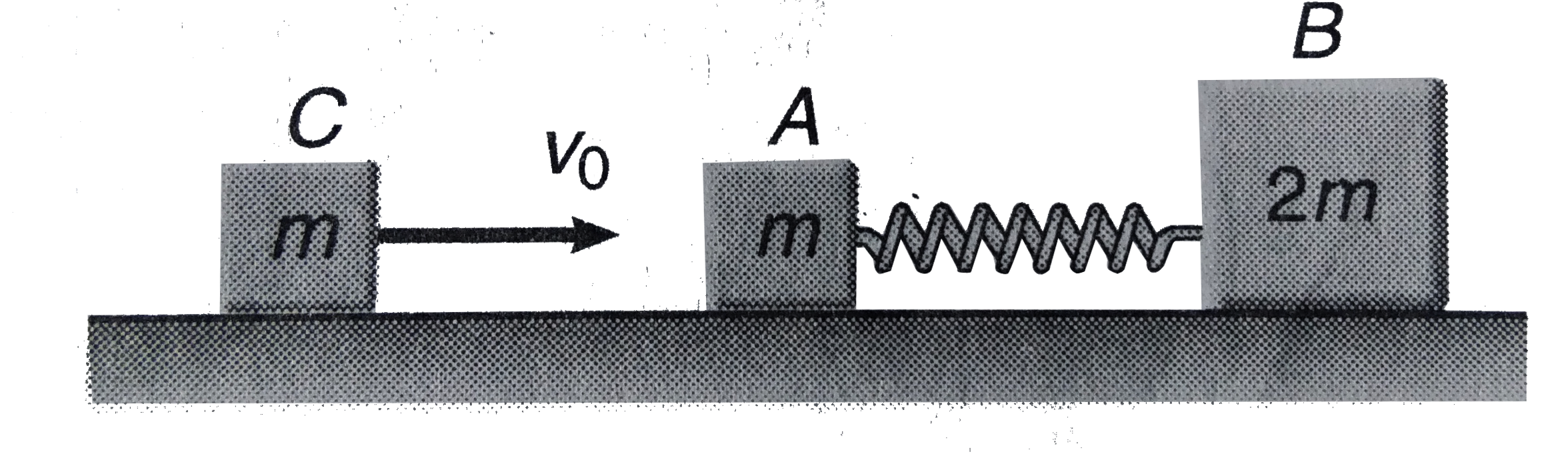
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
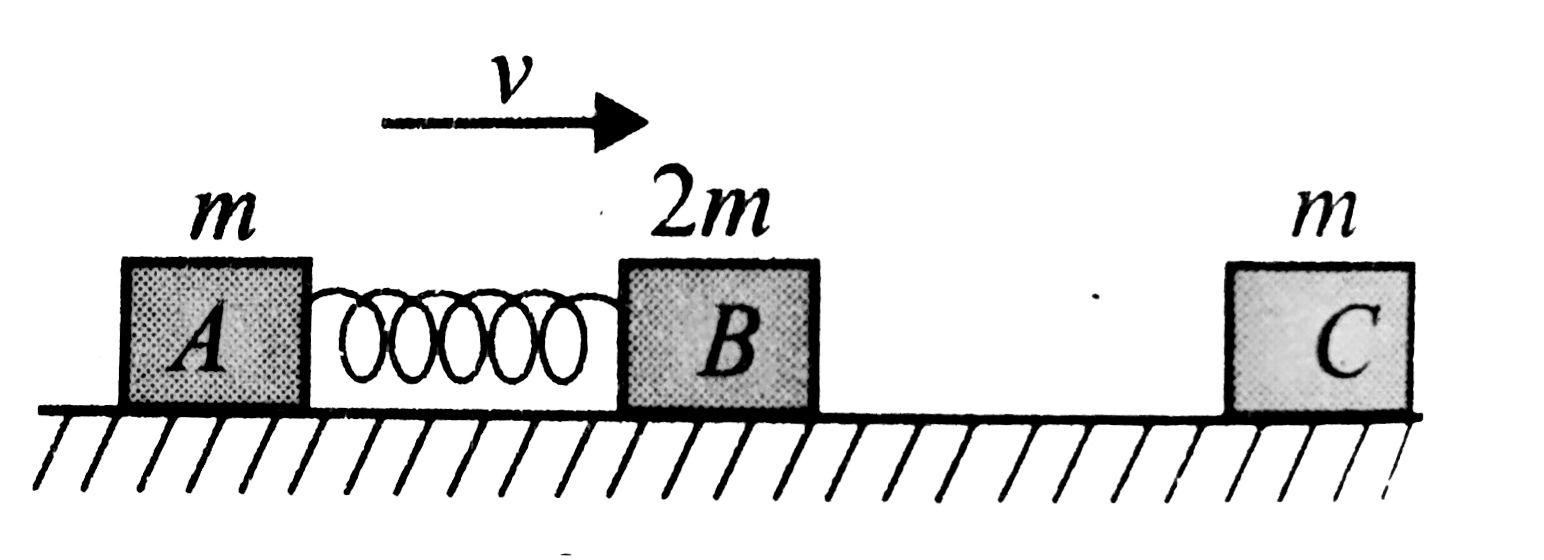
View SolutionTwo identical blocks A and B are connected with a spring of constant k as shown in ligure. If block B s moving rightward with speed V0 maximum extension of spring is
View SolutionTwo blocks A and B of masses in and 2m respectively placed on a smooth floor are connected by a spring. A third body C of mass m moves with velocity v0 along the line joining A and B and collides elastically with A. At a certain instant of time after collision it is found that the instantaneous velocities of A and B are same then:

View Solution

