Question

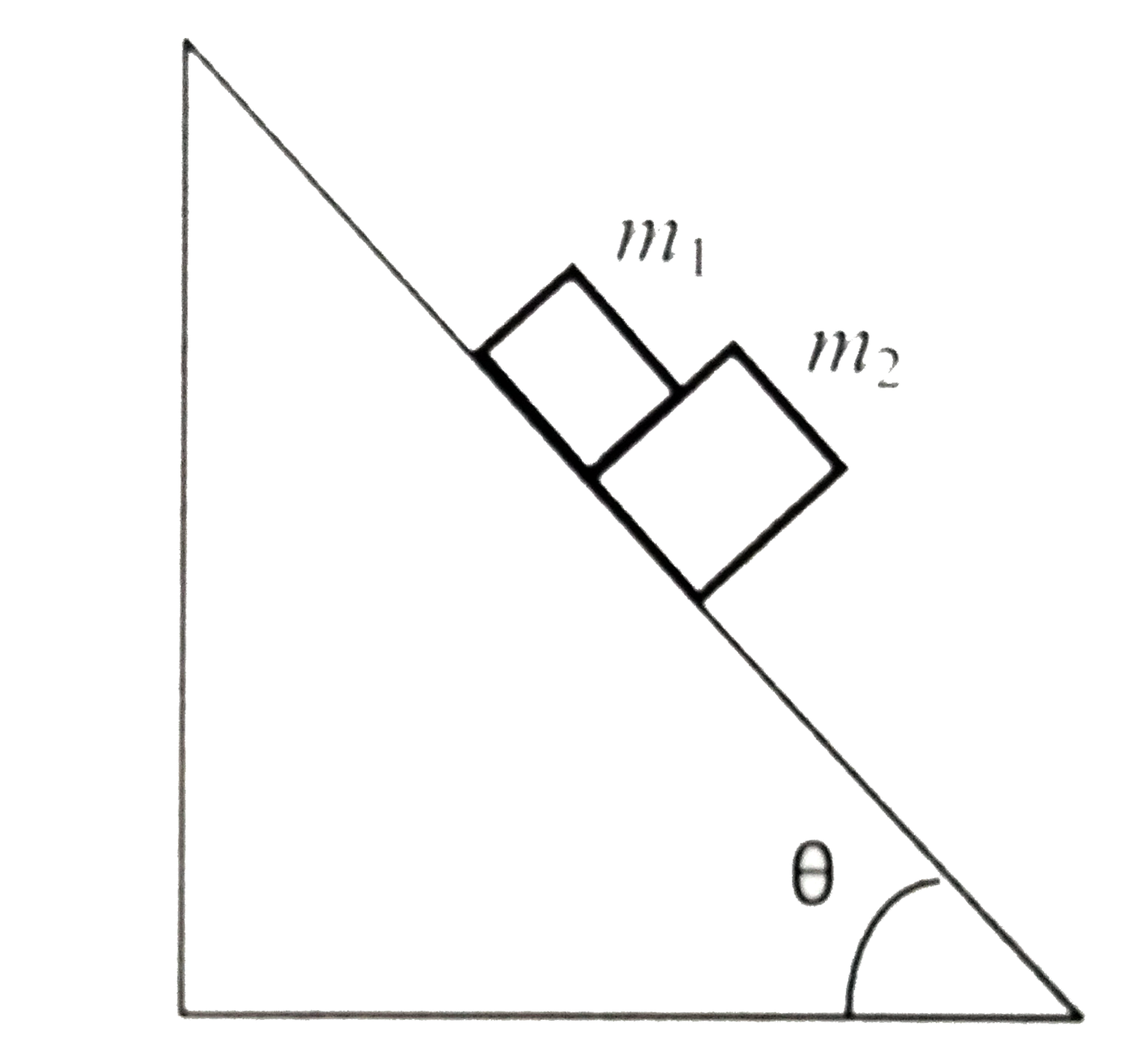
A block of mass $m_1=1kg$ and another mass $m_2=2kg$ are placed together(see figure) on an inclined plane with angle of inclination $\theta$ varius value of $\theta$ are given in list 1 The coefficient of friction between the block $m_1$ and the plank is always zero The coefficient of static and dynamic friction between the block $m_2$ and the plank are equal to $\mu =0.3$ In List II experssions for the friction the block $m_2$ are given Match the correct experssions of the frictionless in List II with the angle given in list 1 and choice the correct option The acceleration due too gravity detented by g
[Useful information $\tan \left({5.5}^{\circ }\right)=0.1\tan \left({11.5}^{\circ }\right)=0.2\tan \left({16.5}^{\circ }\right)=0.3]$
List I
P. $\theta =5^{\circ }$ Q. $\theta ={10}^{\circ }$
R. $\theta ={15}^{\circ }$ S. $\theta ={20}^{\circ }$
List 2

1.$m_{2}g\sin \theta$ 2.$(m_1+m_2)g\sin \theta$
3.$\mu m_{2}g\cos \theta$ 4. $\mu (m_1+m_2)g\cos \theta$

Options

A. a. `P-1, Q-1,R-1,S-3`
B. b. `P-2, Q-2,R-2,S-3`
C. c.`P-2, Q-2,R-2,S-4`
D. d. `P-2, Q-2,R-3,S-3`

Answer

d

Explanation

To solve the problem step by step, we will analyze the forces acting on the blocks on the inclined plane and determine the correct expressions for the frictional force based on the given angles.

Step 1: Understand the Forces Acting on the Blocks
- We have two blocks: \( m_1 = 1 \, \text{kg} \) (block on top) and \( m_2 = 2 \, \text{kg} \) (block on the bottom).
- The angle of inclination is \( \theta \).
- The coefficient of friction between \( m_2 \) and the plank is \( \mu = 0.3 \).
- The friction between \( m_1 \) and the plank is zero.

Step 2: Identify the Forces on Block \( m_2 \)
- The gravitational force acting on \( m_2 \) is \( m_2 g \).
- The component of the gravitational force acting down the incline is \( m_2 g \sin \theta \).
- The normal force acting on \( m_2 \) is \( N = m_2 g \cos \theta \).

Step 3: Determine the Condition for No Slipping
For block \( m_2 \) to not slip, the frictional force must balance the component of the gravitational force acting down the incline. The frictional force \( f \) can be expressed as:
\( f \leq \mu N = \mu m_2 g \cos \theta \)

Setting the forces equal for the case of static friction:
\( f = m_2 g \sin \theta \)

Step 4: Set Up the Inequality
For no slipping:
\( m_2 g \sin \theta \leq \mu m_2 g \cos \theta \)

Dividing through by \( m_2 g \) (assuming \( g \neq 0 \)):
\( \sin \theta \leq \mu \cos \theta \)

Step 5: Convert to Tangent Form
Using the identity \( \tan \theta = \frac{\sin \theta}{\cos \theta} \):
\( \tan \theta \leq \mu \)

Step 6: Substitute the Values
Substituting \( \mu = 0.3 \):
\( \tan \theta \leq 0.3 \)

Step 7: Calculate the Corresponding Angles
Using the given values:
- \( \tan(5.5^\circ) = 0.1 \)
- \( \tan(11.5^\circ) = 0.2 \)
- \( \tan(16.5^\circ) = 0.3 \)

From this, we can conclude:
- For \( \theta = 5^\circ \) and \( \theta = 10^\circ \), \( \tan \theta < 0.3 \), so the frictional force is given by \( m_2 g \sin \theta \).
- For \( \theta = 15^\circ \) and \( \theta = 20^\circ \), \( \tan \theta \geq 0.3 \), so the frictional force is given by \( \mu m_2 g \cos \theta \).

Step 8: Match the Expressions
Now we match the expressions from List II:
- For \( P: \theta = 5^\circ \) and \( Q: \theta = 10^\circ \), the expression is \( m_2 g \sin \theta \) (Expression 1).
- For \( R: \theta = 15^\circ \) and \( S: \theta = 20^\circ \), the expression is \( \mu m_2 g \cos \theta \) (Expression 3).

Final Matching:
- \( P \) (5°) → Expression 1: \( m_2 g \sin \theta \)
- \( Q \) (10°) → Expression 1: \( m_2 g \sin \theta \)
- \( R \) (15°) → Expression 3: \( \mu m_2 g \cos \theta \)
- \( S \) (20°) → Expression 3: \( \mu m_2 g \cos \theta \)

Summary of the Solution:
- \( P \) matches with Expression 1
- \( Q \) matches with Expression 1
- \( R \) matches with Expression 3
- \( S \) matches with Expression 3