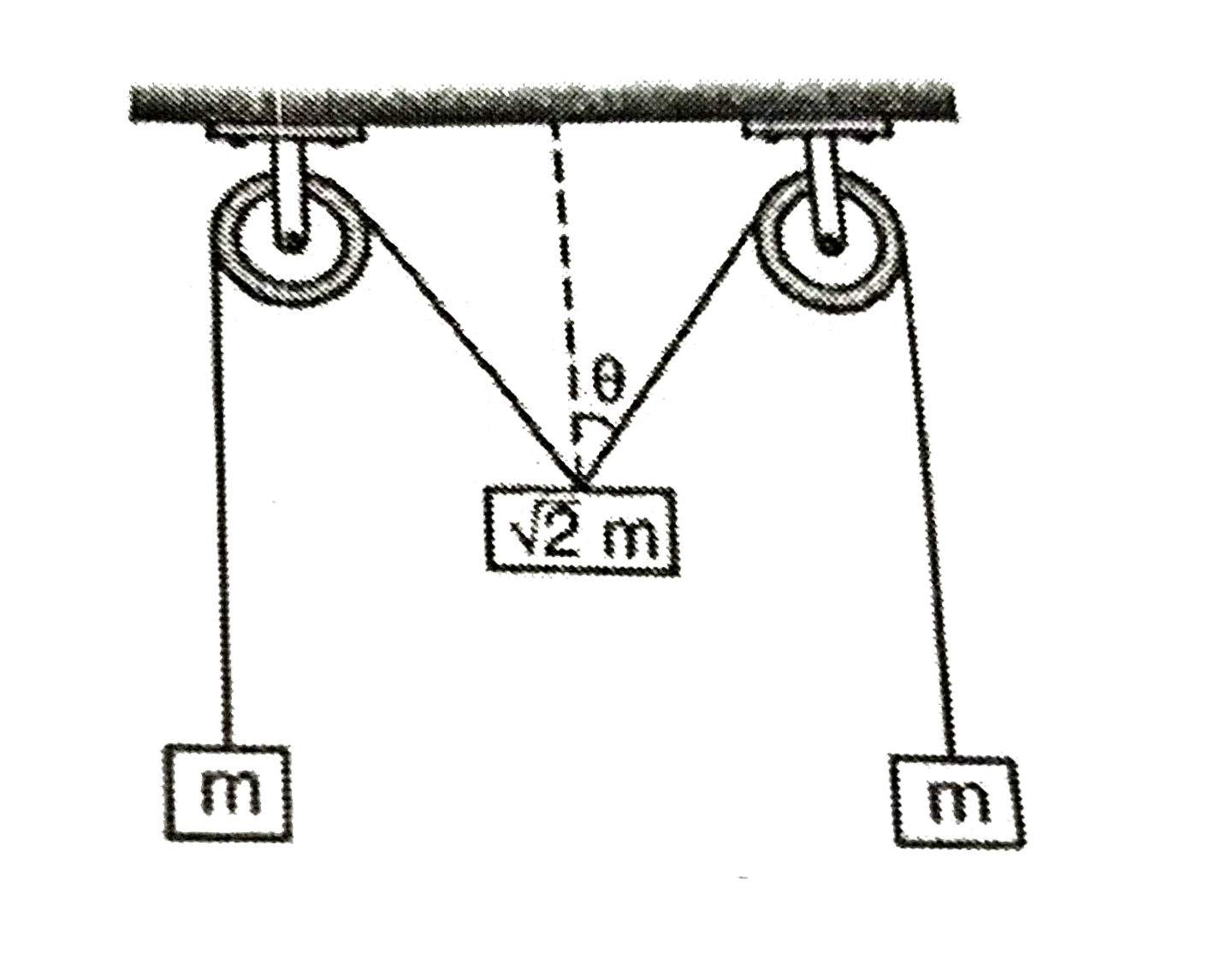
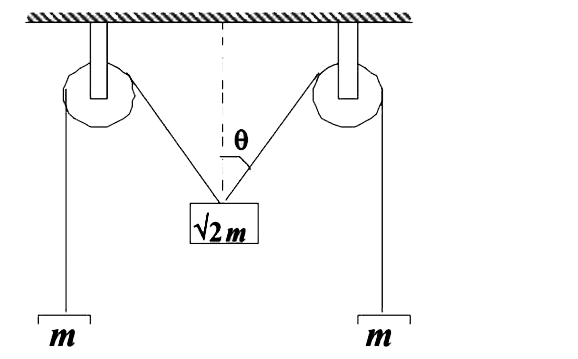
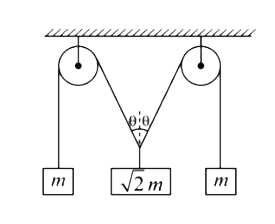
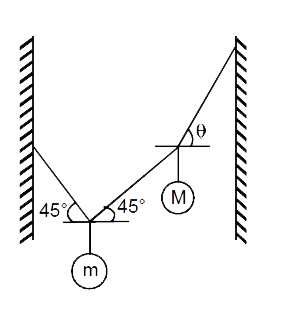
The pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle θ should be
0∘
30∘
45∘
60∘
The correct Answer is:c
For equilibrium in vertical direction for body B we have

√2mg=2Tcosθ
=2(mg)cosθ
T=mg(at equilibrium )
∴Cosθ=1√2⇒θ=45∘
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple correct answer type
3 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Assertion -reasoning
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - True And False
4 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Knowledge Check
The pulley and strings shown in fig 15.3.16 are smooth and of negligible mass. For the system to remiain in equilibrium the angle θ should be
 AzeroB30∘C45∘D60∘
AzeroB30∘C45∘D60∘
The pulley and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle θ should be:
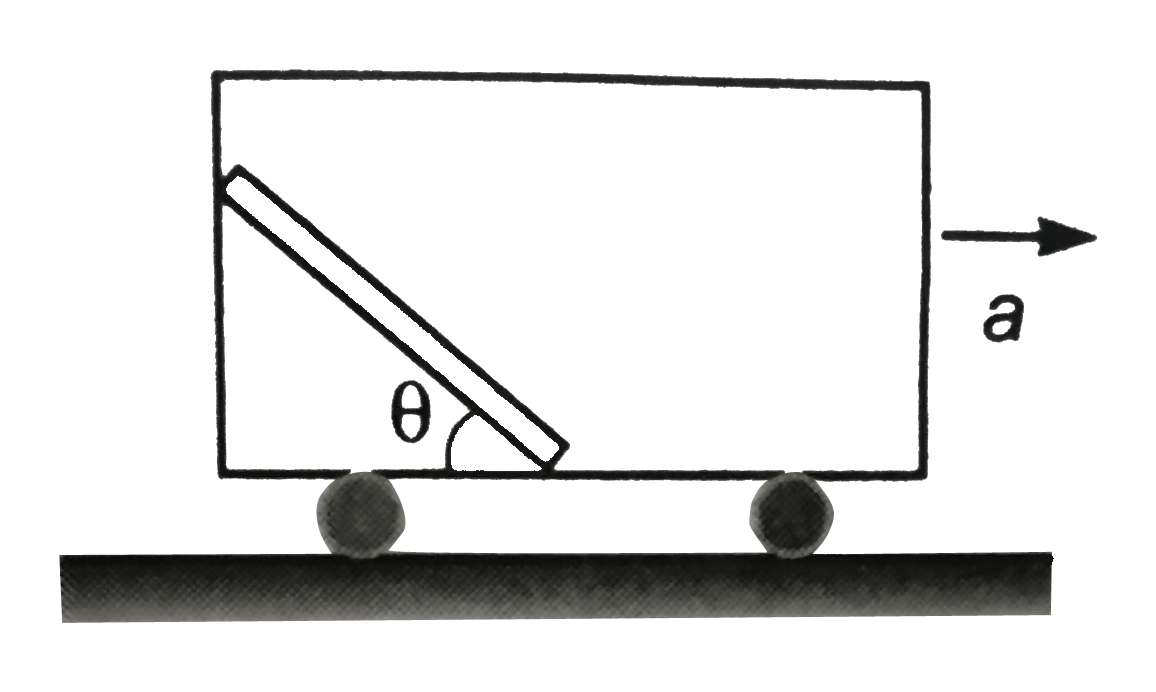
View SolutionA smooth rod length l is kept inside a trolley at an angle θ as shown in the figure. What should be the acceleration a of the trolley so that the rod remain in equilibrium with respect to it?
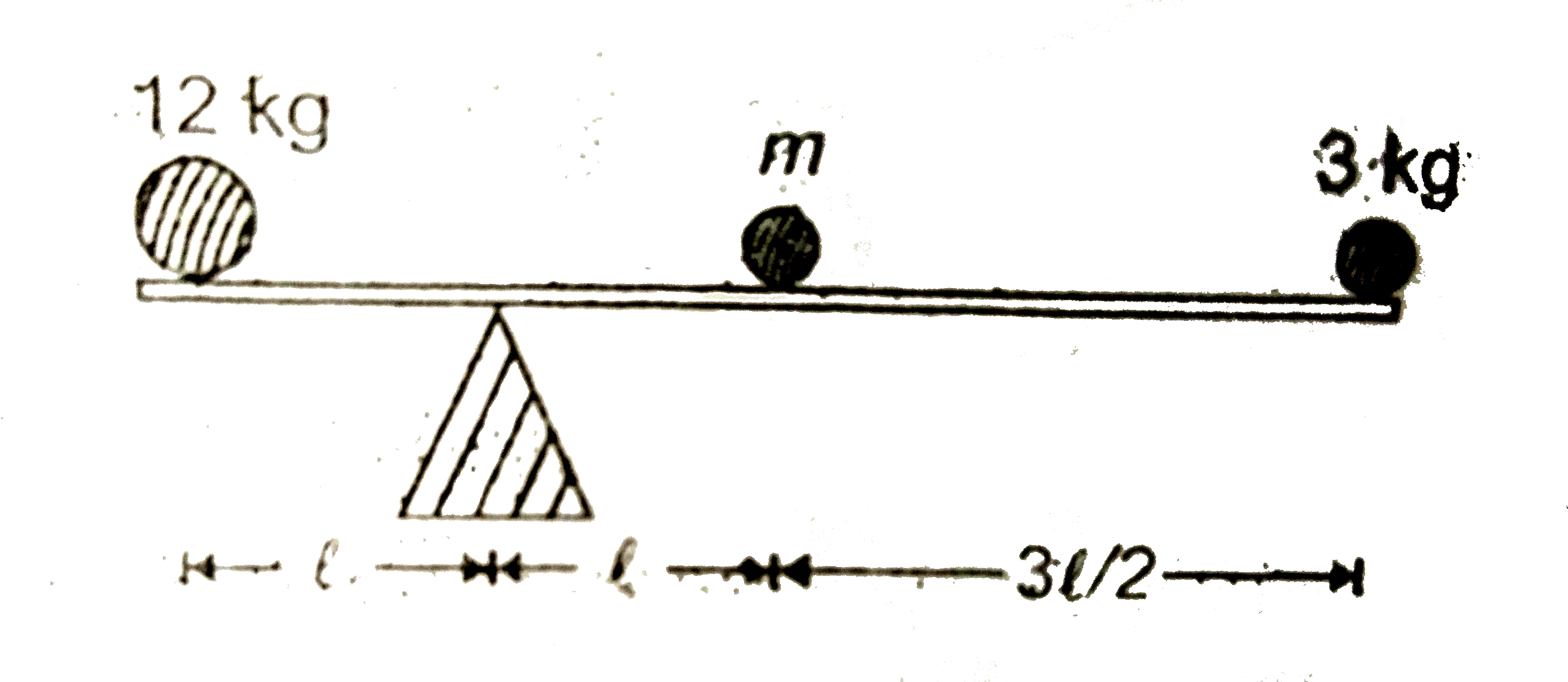
View SolutionFor the system shown in figure , to be in equilibrium , determine mass m .
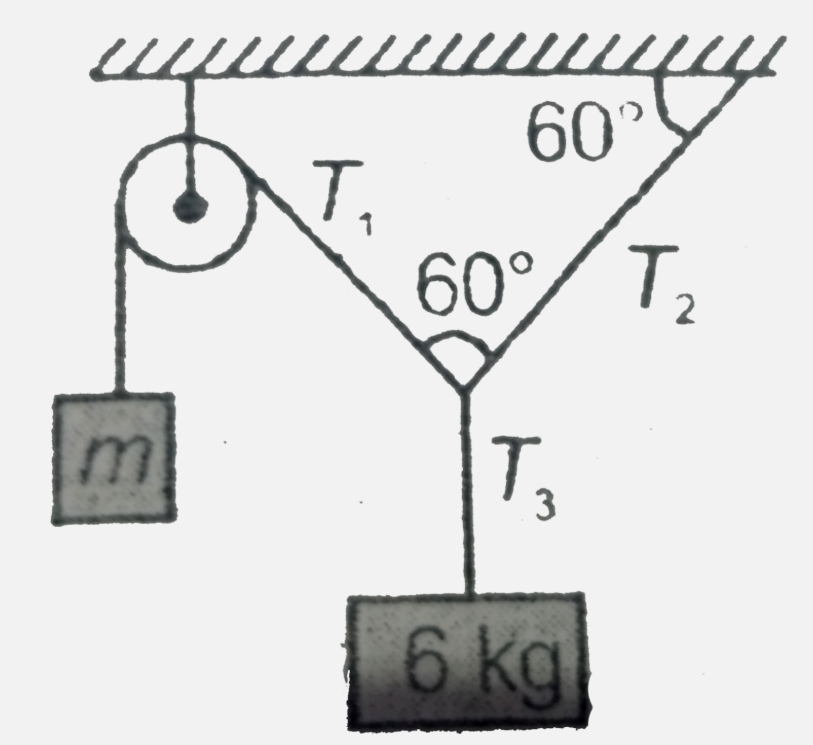
View SolutionFor the system shown in figure, the tensions in the string
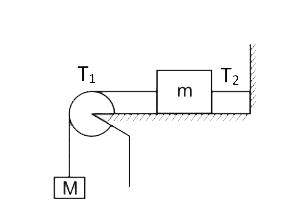
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
View SolutionFor the equilibrium of the system shown, the value of mass m should be
View SolutionThree masses m1=m,m2=2mandm3=3m are hund on a string passing over a frictionless pulley as shown in Figure . The mass of the string in negligible . The system is released from rest.
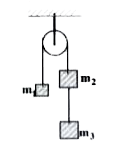
The tension in the string between masses m2andm3 is
View Solution