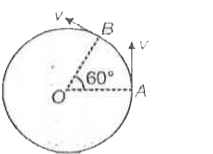
A particle is moving in a circle of radius r centred at O with constant speed v. What is the change in velocity in moving from AtoB(∠AOB=40∘) ?
2vsin20∘
4vsin40∘
2vsin40∘
vsin20∘
The correct Answer is:A
To find the change in velocity of a particle moving in a circle from point A to point B, where the angle ∠AOB is 40 degrees, we can follow these steps:
1. Identify the Initial and Final Velocities:
- Let the initial velocity at point A be →v1 and the final velocity at point B be →v2.
- Since the particle is moving with constant speed v, we have:
|→v1|=|→v2|=v
2. Determine the Angle Between the Velocities:
- The angle between the two velocity vectors →v1 and →v2 is given as θ=40∘.
3. Use the Formula for Change in Velocity:
- The change in velocity Δ→v can be calculated using the formula:
|Δ→v|=|→v2−→v1|
- This can be expressed using the cosine rule:
|Δ→v|=√|→v1|2+|→v2|2−2|→v1||→v2|cosθ
4. Substituting the Values:
- Since |→v1|=|→v2|=v:
|Δ→v|=√v2+v2−2vvcos(40∘)
- Simplifying this:
|Δ→v|=√2v2−2v2cos(40∘)
- Factor out 2v2:
|Δ→v|=√2v2(1−cos(40∘))
5. Using the Identity for Sine:
- We can use the identity 1−cos(θ)=2sin2(θ2):
1−cos(40∘)=2sin2(20∘)
- Therefore:
|Δ→v|=√2v2⋅2sin2(20∘)=√4v2sin2(20∘)
6. Final Expression for Change in Velocity:
- Taking the square root:
|Δ→v|=2vsin(20∘)
Conclusion:
The change in velocity as the particle moves from point A to point B is:
|Δ→v|=2vsin(20∘)
- Let the initial velocity at point A be →v1 and the final velocity at point B be →v2.
- Since the particle is moving with constant speed v, we have:
|→v1|=|→v2|=v
- The angle between the two velocity vectors →v1 and →v2 is given as θ=40∘.
- The change in velocity Δ→v can be calculated using the formula:
|Δ→v|=|→v2−→v1|
- This can be expressed using the cosine rule:
|Δ→v|=√|→v1|2+|→v2|2−2|→v1||→v2|cosθ
- Since |→v1|=|→v2|=v:
|Δ→v|=√v2+v2−2vvcos(40∘)
- Simplifying this:
|Δ→v|=√2v2−2v2cos(40∘)
- Factor out 2v2:
|Δ→v|=√2v2(1−cos(40∘))
- We can use the identity 1−cos(θ)=2sin2(θ2):
1−cos(40∘)=2sin2(20∘)
- Therefore:
|Δ→v|=√2v2⋅2sin2(20∘)=√4v2sin2(20∘)
- Taking the square root:
|Δ→v|=2vsin(20∘)
The change in velocity as the particle moves from point A to point B is:
|Δ→v|=2vsin(20∘)
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning
5 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective
40 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A particle is moving in a circle of radius r centred at O with constant speed u. What is the change in velocity in moving from AtoB(∠AOB=40∘) ?
View SolutionA particle is moving in a circle of radius r having centre at O with a constant speed v . The magnitude of change in velocity in moving from A to B is
View Solution
Knowledge Check
A particle is moving on a circular path with a constant speed v. Its change of velocity as it moves from A to B is:
 A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.A particle is moving in a circle with uniform speed. IT has constant
AvelocityBAccelerationCkinetic energyDdisplacement
A particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
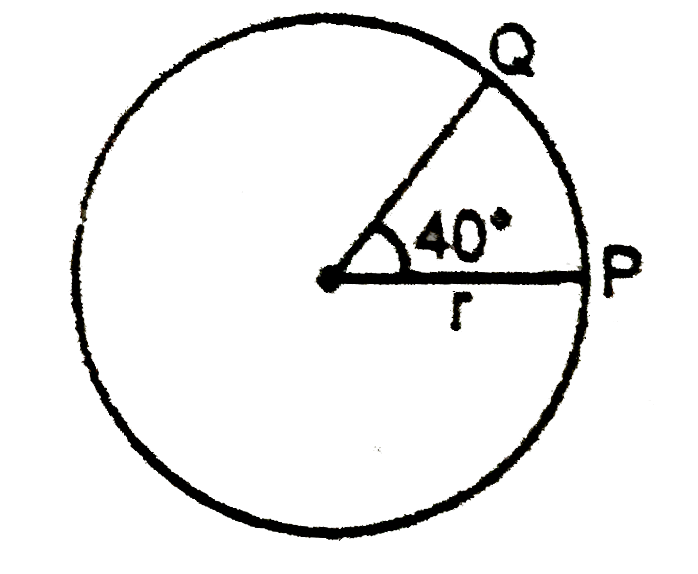
View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
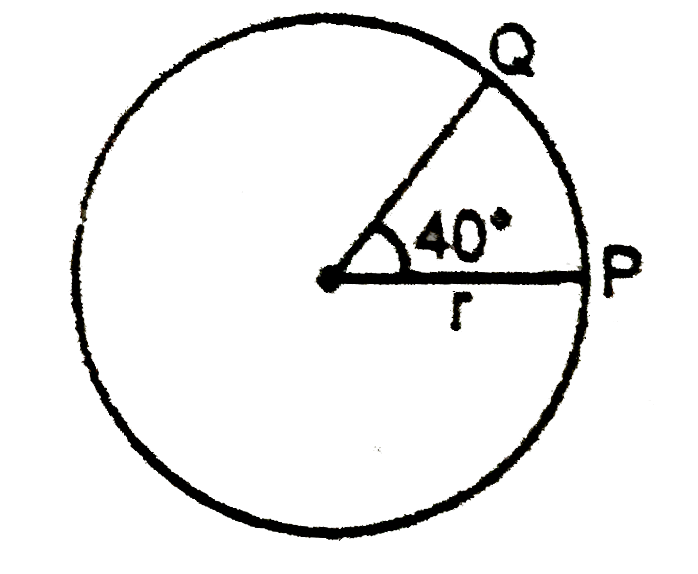
View SolutionA particle is moving on a circular path with constant speed v then the change in its velocity after it has described an angle of 60∘ will be
View SolutionA particle is moving on a circular path with constant speed v. The magnitude of the change in its velocity after it has described an angle of 90∘ is :
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View Solution
