Find the angular velocity of A with respect to B in (Fig. 5.156).
 .
.
Angular velocity of A with respect to B ,
ωAB=(VAB)⊥rAB
⇒(VAB)⊥=VAsinθ1+VBsinθ2
⇒rAB=r
ωAB=vAsinθ1+vBsinθ2r.
 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Particles AandB move with constant and equal speeds in a circle as shown in (Fig. 5.164). Find the angular velocity of the particle A with respect to B, if the angular velocity of particle Aw.r.t.O is ω.
 .
.
View SolutionFind the angular velocity of A with respect to O at the instant shown in (Fig. 5.165).
 .
.
View SolutionTwo particles A and B are situated at a distance d=2m apart. Particle A has a velocity of 10m/s at an angle of 60∘ and particle B has a velocity v at an angle 30∘ as shown in figure. The distance d between A and B is constant. the angular velocity of B with respect to A is :
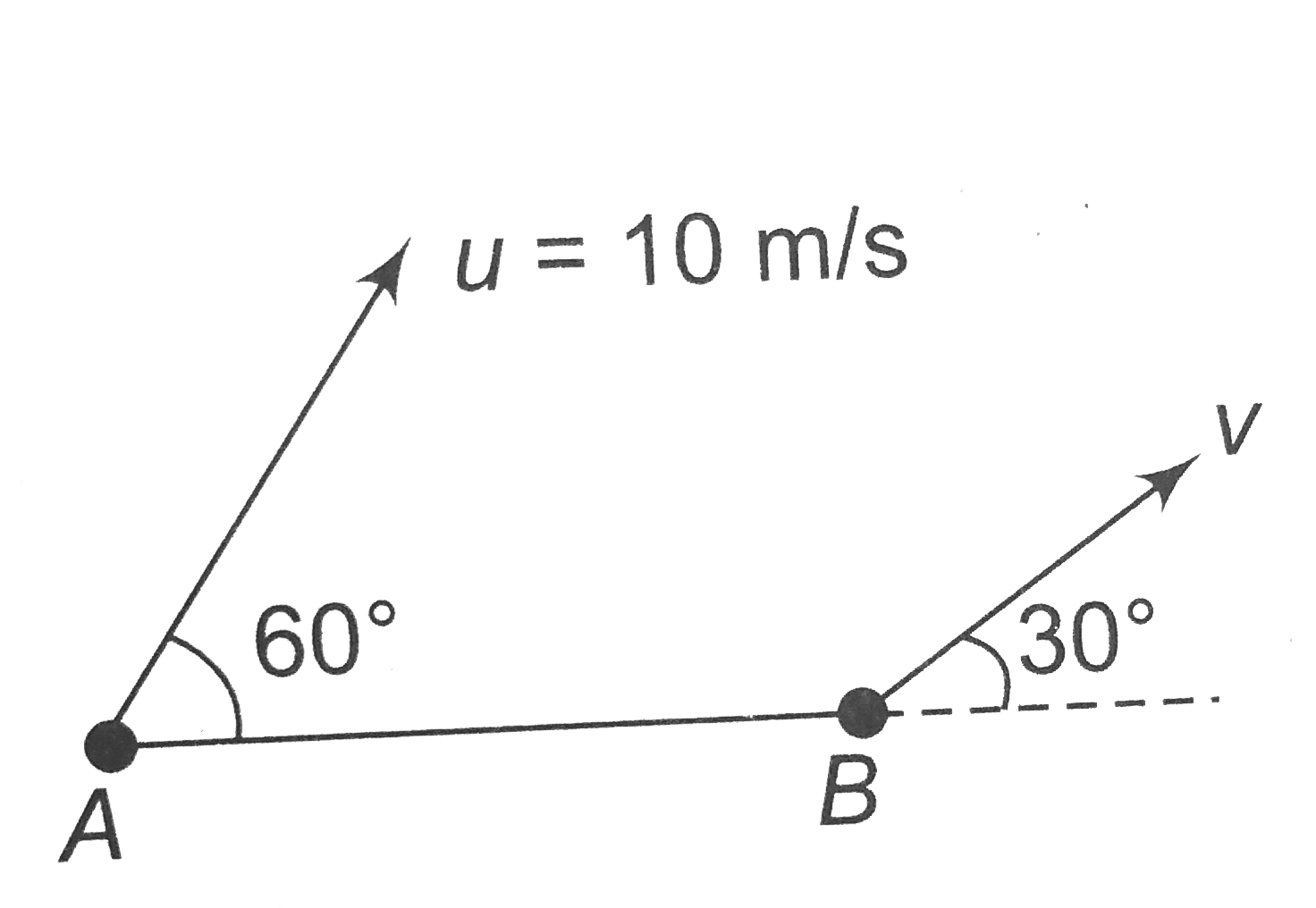 .
.
View SolutionThe angular velocity of a particle moving in a circle realative to the center of the circle is equal to ω. Find the angular velocity of the particle relative to a point on the circular path.
View SolutionTwo men A and B are sitting at th eend of a plank of length L, if plank is rotating with angular velocity ω about an axis perpendicular to its length and passing through a point at a distance of L/3 from A. The angular velocity of B with respect to A is
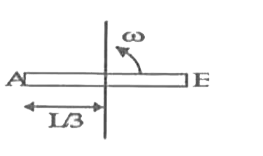
View SolutionTwo particles A and B are moving with constant velocities V1=ˆj and v2=2ˆi respectively in XY plane. At time t=0, the particle A is at co-ordinates (0,0) and B is at (-4,0). The angular velocities of B with respect to A at t=2s is (all physical quantities are in SI units)
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?

View SolutionConsdier the situation shown in figure
(I ) find out velocity of B with respect to A
(ii ) Find out velocity of A with respect to B

View SolutionA rod of length l is moving in a vertical plane (x−y) when the lowest point A of the rod is moved with a velocity v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionFig. shows a ball having a charge q fixed at a point A. Two identical balls of mass m having charge +qand−q are attaached to the end of a light rod of length 2a. The system is released from the situation shown in fig. Find the angular velocity of the rod when the rod turns through 90∘
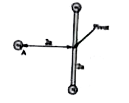
View Solution
