An aeroplane has a velocity of 110 m/s directed due north and is subjected to a wind blowing from west to east at a speed of 40 m/s . Calculate the actual velocity of the aeroplane relative to the earth .
Velocity of helicopter w.r.t. groundn is given by
→VHelicopter,air=→VHelicopter,air+→VAir=→VAir+→VHelicopter,air
∣∣→VHA∣∣=nu,∣∣→VA∣∣=u,∣∣→VH∣∣=V
Hence, the actual velocity of helicopter is the vector sum of its velocity of helicopter relative to air and velocity of air.
Using cosine rule, for motion from A→B,
n2u2=u2+v2−2uvcosθ
or v2−2uvcosθ=u2(n2−1)
or (v−ucosθ)2=u2(n2−1)+u2cos2θ
=u2(n2−sin2θ)
v−ucosθ=±u√n2−sin2θ
v=ucosθ±u√n2−sin2θ
As n≥1,
n2−sin2θ≥1−sin2θ≥cos2θ
Hence, speed of helicoper is v=ucosθ+u√n2−sin2θ)
Now we consider motion from B to A.
Similar to first case, the helicopter will return to AalongBA when its velocity after being deflected by wind is along BA.
Once again using consine rule inthe vector triangle, we get
n2u2=u2+V2−2uVcos(180∘−θ)
=u2+V2+2uVcosθ
V=−ucosθ+u√n2−sin2θ
The total time for motion A to B and B to A,
t=dv+dV
=d(u+V)uV
=2du√n2−sin2θu2(n2−sin2θ)−u2cos2θ
=2du√n2−sin2θu2(n2−1)=2d√n2−sin2θu(n2−1).
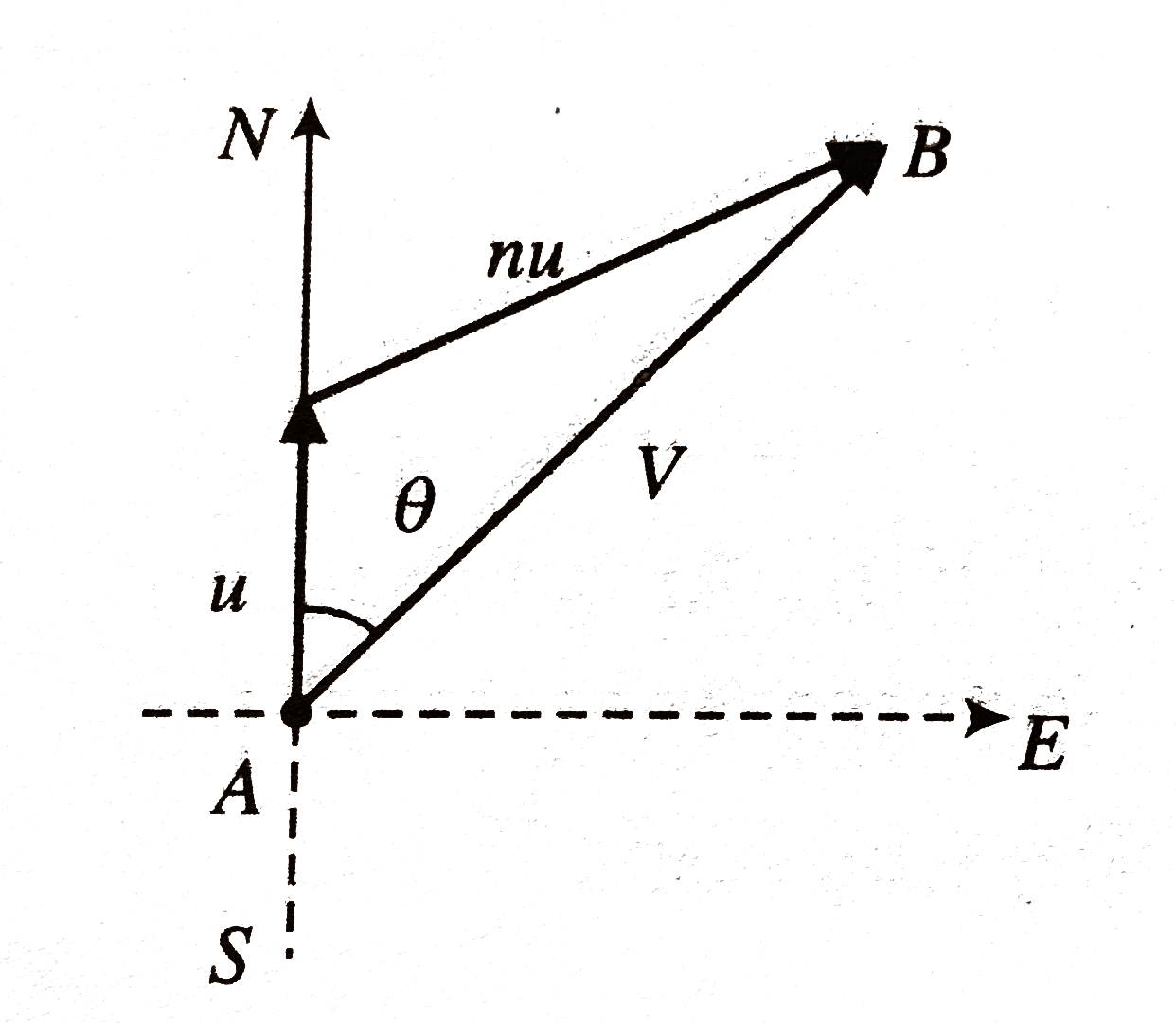 ,
, 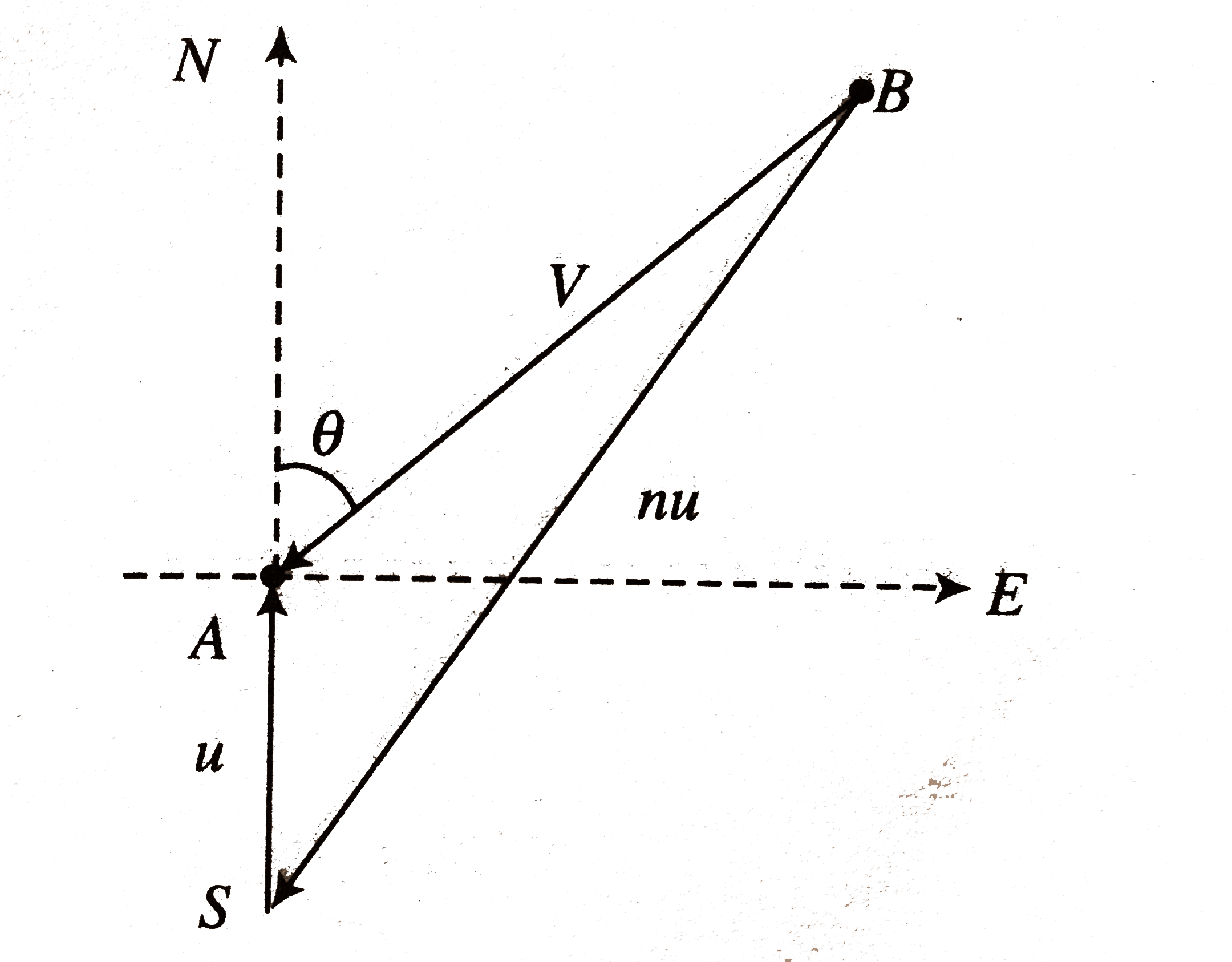 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
An aeroplane is flying with the velocity of V1 =800 kmph relative to the air towards south. A wind with velocity of V2=15ms−1 is blowing from West to East. What is the velocity of the aeroplane with respect to the earth.
View SolutionAn aeroplane is flying with a velocity 800kmph relative to air wind is belong from west to east with a velocity 15ms−1. Find velocity of aeroplane relative to the earth to fly south ward
View SolutionA ship is steaming towards east with a speed of 8 m/s. A women runs across the deck at a speed of 6ms−1 towards north. What is the velocity of the women relative to the sea ?
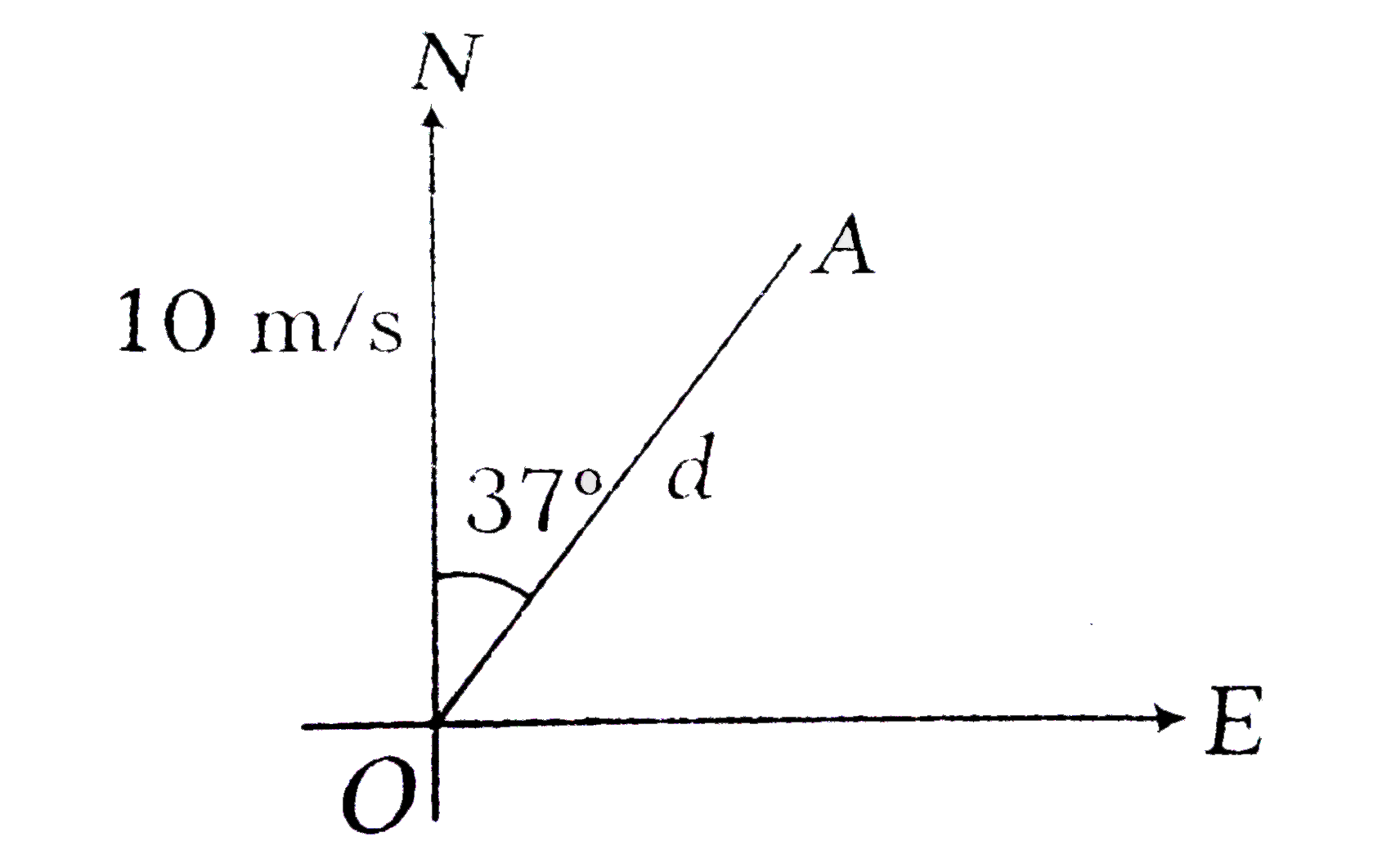
View SolutionAn aeroplane has to go from a point O to another point A, at distance d due 37∘ East of North. A wind is blowing due North at a speed of 10ms−1. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
View SolutionRain is falling at the speed of 25√3m/s vertically. The wind blows west to east at a speed of 25 m/s. find the velocity of rain as experienced by a person standing on the ground.
View SolutionA plane moves in windy weather due east while the pilot the plane somewhat south of east. The wind is blowing at 50 km/h directed 30∘ east of north, while the palne moves at 200 km/h relative to the wind . What is the velocity of the plane relative to the ground and what is the direction in which the pilot points the palne ?
View SolutionAn observer is travelling in west with velocity of 5 km/h and observes that wind is blowing in north with the velocity of 5√3 km/h. Find out the actual velocity of wind.
View SolutionA motor car A is travelling with a velocity of 20 m/s in the north-west direction and another motor car B is travelling with a velocity of 15 m/s in the north-east direction. The magnitude of relative velocity of B with respect to A is
View SolutionRam moves in east direction at a speed of 6 m/s and Shyam moves 30∘ east of north at a speed of 6 m/s. The magnitude of their relative velocity is
View SolutionAn aeroplane has to go from a point P to another point Q, 1000 km away due north. Wind is blowing due east at a speed of 200km/h. The air speed of plane is 500km/h.
(a) Find the direction in which the pilot should head the plane to reach the point Q.
(b) Find the time taken by the plane to go from P to Q.
View Solution
