A body has maximum range R1 when projected up the plane. The same body when projected down the inclined plane, it has maximum range R2. Find the maximum horizontal range. Assume equal speed of projection in each case and the body is projected onto the inclined plane in the line of the greatest slope.
To solve the problem, we need to find the maximum horizontal range of a body projected up and down an inclined plane, given that the body has maximum ranges R1 and R2 when projected up and down the incline, respectively.
1. Understanding the Ranges:
- When a body is projected up the inclined plane, the maximum range R1 is given by the formula:
R1=u2g(1+sinθ)
- When the same body is projected down the inclined plane, the maximum range R2 is given by:
R2=u2g(1−sinθ)
2. Finding the Relationship:
- We want to find the maximum horizontal range Rmax. The relationship between the ranges can be established using the following equation:
1R1+1R2=gu2
3. Substituting the Ranges:
- Substitute the expressions for R1 and R2 into the equation:
1u2g(1+sinθ)+1u2g(1−sinθ)=gu2
4. Simplifying the Equation:
- This simplifies to:
gu2(1+sinθ)+gu2(1−sinθ)=gu2
- Multiplying through by u2g gives:
11+sinθ+11−sinθ=1
5. Finding Maximum Horizontal Range:
- The maximum horizontal range Rmax can be derived from the relationship:
Rmax=R1R2R1+R2⋅2
- This is based on the harmonic mean of R1 and R2.
6. Final Expression:
- Thus, the maximum horizontal range is given by:
Rmax=2R1R2R1+R2
Final Answer:
The maximum horizontal range Rmax when a body is projected up and down an inclined plane is:
Rmax=2R1R2R1+R2
- When a body is projected up the inclined plane, the maximum range R1 is given by the formula:
R1=u2g(1+sinθ)
- When the same body is projected down the inclined plane, the maximum range R2 is given by:
R2=u2g(1−sinθ)
- We want to find the maximum horizontal range Rmax. The relationship between the ranges can be established using the following equation:
1R1+1R2=gu2
- Substitute the expressions for R1 and R2 into the equation:
1u2g(1+sinθ)+1u2g(1−sinθ)=gu2
- This simplifies to:
gu2(1+sinθ)+gu2(1−sinθ)=gu2
- Multiplying through by u2g gives:
11+sinθ+11−sinθ=1
- The maximum horizontal range Rmax can be derived from the relationship:
Rmax=R1R2R1+R2⋅2
- This is based on the harmonic mean of R1 and R2.
- Thus, the maximum horizontal range is given by:
Rmax=2R1R2R1+R2
The maximum horizontal range Rmax when a body is projected up and down an inclined plane is:
Rmax=2R1R2R1+R2
Topper's Solved these Questions
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Solved Examples
Explore 7 Videos
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise 5.1
Explore 15 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Integer
Explore 9 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICS ENGLISHChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
Similar Questions
If the maximum vertical height and horizontal ranges of a projectile are same, the angle of projection will be
View SolutionFor a given velocity of projection from a point on the inclined plane, the maximum range down the plane is three times the maximum range up the incline. Then find the angle of inclination of the inclined plane.
View Solution
Knowledge Check
If R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is
Atan−1(HR)Btan−1(2HR)Ctan−1(4HR)Dtan−1(4HH)
The horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is
View Solution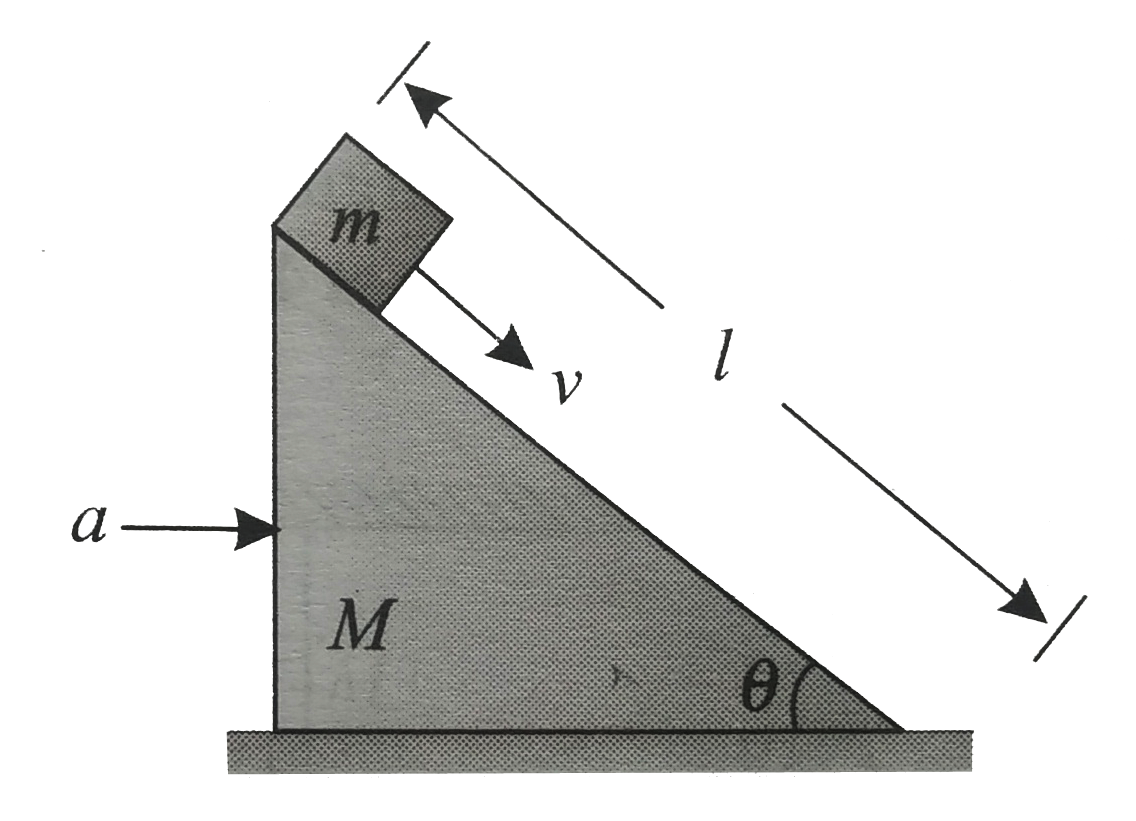
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View SolutionThe range of a projectile at an angle θ is equal to half of the maximum range if thrown at the same speed. The angel of projection θ is given by
View SolutionThe range of a projectile at an angle θ is equal to half of the maximum range if thrown at the same speed. The angel of projection θ is given by
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionA body is projected with velocity u such that in horizontal range and maximum vertical heights are same.The maximum height is
View SolutionA body is projected with kinetic energy E such that its range is maximum. Its potential energy at the maximum height is
View Solution
