Question

A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If $\alpha \text{and}\beta$ be the base angles and $\theta$ the angle of projection, prove that $\tan \theta =\tan \alpha +\tan \beta$ .

Explanation

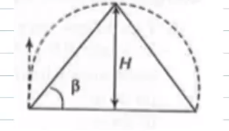
Let `ABC` be the triangle with base `BC`. Let `h` be the height of the vertex `A` above `BC`. If `AM` is the perpendicular drawn on base `BC` from vertex `A`, then `tan prop = h//a` and `tan beta = H//B,` where `BM = a and CM = b`.
Since `A(a,h)` lies on the trajectory of the projectile,
`y = x tan theta (1 - (x)/(R ))` ...(i)
Therefore, it should satisfy (i) i.e.,
`h = a tan theta (1 - (a)/(a + b)) [because Range, R = a + b]`
`(h)/(a) = tan theta [(b)/(a + b)]`
`rArr tan theta = (h)/(a) + (h)/(b) = tan prop + tan beta`
Hence, proved.
.