Question

Two balls are dropped from the top of a hight tower with a time interval of $t_0$. Second , where $t_0$ is smaller than the time taken by the first ball to reach the ground which is perfectly inelastic. The distance $S$ between the two balls plotted against the time lapse $t$ from the instant of dropping the second ball, is best tepresented by.

Options

A. .
B. .
C. .
D. .

Answer

D

Explanation

To solve the problem, we need to analyze the motion of two balls dropped from a tower at different times and determine how the distance $$S$$ between them changes over time after the second ball is dropped.

1. Understanding the Problem:
- Let the first ball be dropped at \( t = 0 \).
- The second ball is dropped after a time interval \( t_0 \).
- We need to find the distance \( S \) between the two balls as a function of time \( t \) after the second ball is dropped.

2. Equations of Motion:
- For the first ball (dropped at \( t = 0 \)):
\( S_1 = \frac{1}{2} g t^2 \quad \text{(where \( t \) is the time since the first ball was dropped)}
\)
- For the second ball (dropped at \( t = t_0 \)):
\( S_2 = \frac{1}{2} g (t - t_0)^2 \quad \text{(where \( t \) is the time since the second ball was dropped)}
\)

3. Calculating the Distance Between the Balls:
- The distance \( S \) between the two balls at time \( t \) after the second ball is dropped is given by:
\( S = S_1 - S_2 \)
- Substituting the equations of motion:
\( S = \frac{1}{2} g (t_0 + t)^2 - \frac{1}{2} g (t)^2 \)

4. Expanding the Equation:
- Expanding \( S_1 \):
\( S_1 = \frac{1}{2} g (t_0^2 + 2t_0t + t^2) \)
- Thus, we have:
\( S = \frac{1}{2} g (t_0^2 + 2t_0t + t^2) - \frac{1}{2} g t^2 \)
- Simplifying:
\( S = \frac{1}{2} g t_0^2 + g t_0 t \)

5. Interpreting the Result:
- The distance \( S \) is a linear function of \( t \) (since \( S \) depends on \( t \) linearly as \( g t_0 t \)).
- The constant term \( \frac{1}{2} g t_0^2 \) represents the initial distance between the two balls when the second ball is dropped.

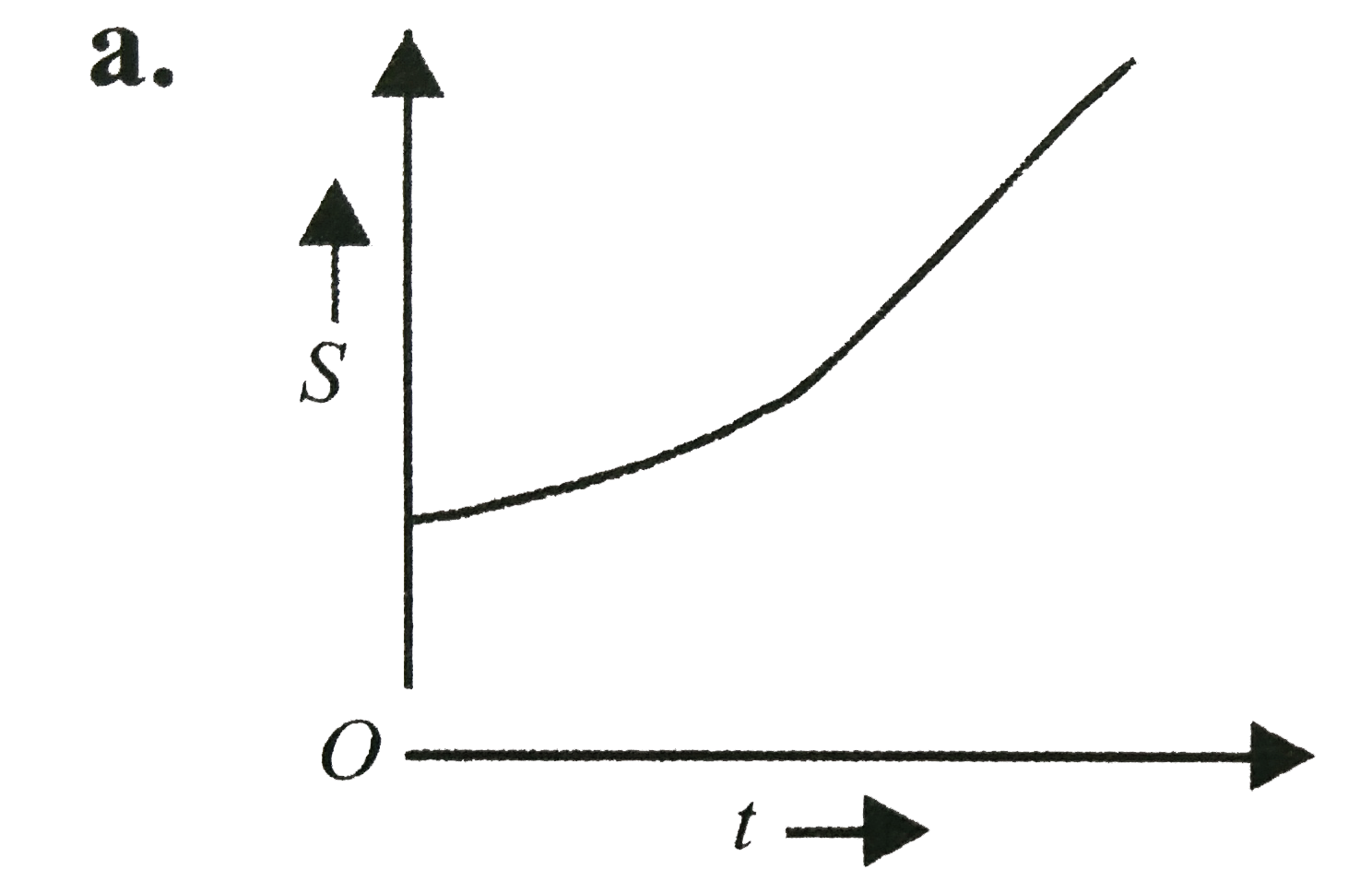
6. Graph Representation:
- The graph of \( S \) versus \( t \) will be a straight line with a positive slope, starting from a positive value \( \frac{1}{2} g t_0^2 \) (the initial distance) and increasing linearly with time.

Conclusion:
The distance \( S \) between the two balls plotted against the time \( t \) from the instant of dropping the second ball is best represented by a linear graph with a positive slope.