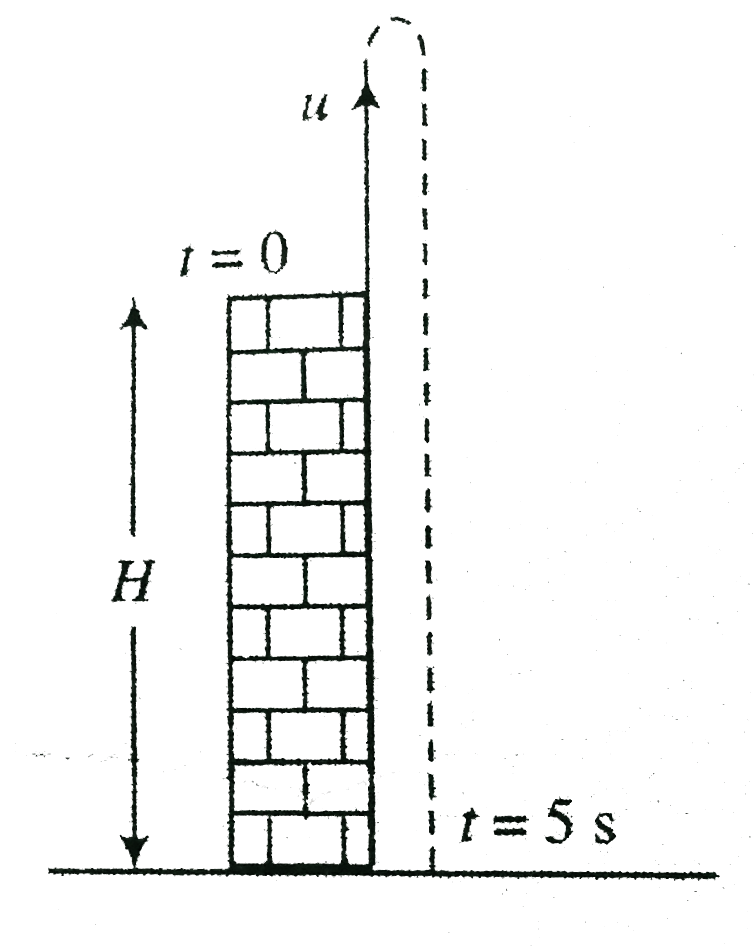
A particle is projected up with initial speed u=10ms−1 from the top of a building at time t=0. At time t=5s the particle strikes the ground. Find the height of the building.
 .
.
Taking oringin at the top of building and upward direction positive.
For particled A u=+10s−1a=−10ms−1
Using y=ut+12at2
=10t−12×10×t2)=10t−52 ...(i)
Equation (i) is the equation of parabola open down The parabola passes origin when y=0. hence from
0=10t−5t−2⇒t=0,0s
For velocity-time relation, v=u+at
v=10−10t. (ii)
The relaation is straight line relation with negative slopen and positive intercept.
At maximum hetght, velocity of the particle is zero.
0=10−10t⇒t=1s
Maximum height from (i), ymax=10×1−5×12=5ss−1
It will reach ground wher y=−100m
Using i again, −74=10t−5t2⇒(t−5)(t+3)=0
When given t=5s, i.e., the particle will hit ground at t=5s.
Velocity at the time of hitting
Using (ii), v=10−10×5=40ms−1
For speed-time relation, the speed is always positive the mirror-image of velocity-time relation on positive side.
For drawing acceleration-time graph we have taken downward direction as negative and acceleration is constant throughout the motion of the praticle, i.e. −10ms−(2) Hence, acceleration time graph will be straight line parallel with time axis and below the time axis.
 .
.
d. For particle B:u=−10ms−1a=−20ms−2
Displacement-time relation,
y=−10t−12×t2=−10t2 ...(iii)<br>Itisaparablaopendownanditpassesthroughorig∈.Theparticelwillreachgroundwheny=-75 m<br>From(iii)=-10t-5t^(2)<br>ort^(2)+2t-15=0 rArr t=3 s<br>Thevelocityofthepartic≤∈relationwithtime<br>v=0-10t rArr v=10t...(iv)<br>Thisisastraightl∈ewith¬ativeslopeandpassingthroughorig∈.Thepartic≤reachesoundatt=3 s,velocityofthepartic≤whenithitsgroundis<br>v=-10xx3=-30 m s^(-1)<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V01_C04_S01_056_S02.pngwh=80%mx-autosty≤=background:white;>.<br>Forpartic≤C:u=0. a=-10 m s^(-2)<br>Usingy=ut+(1)/(2)at^(2)<br>=0-(1)/(2)(-10)t^(2)=-5t^(2)<br>Itisaparabolaopendownanditpassesthroughorig∈.<br>Forvelocity−timerelationvec v=vec u+vec at<br>v=0-10 t =-10t..(vi)<br>Straightl∈ewith¬ativeslopepassesthroughorigion.<br>Itwillreachroundaty=-75 m<br>-75=-5t^(2) rArr t=sqrt15 s<br>Velocityatthetimewhenitreachesgroundv=-10sqrt15 s.
 .
.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A particle is projected up with initial speed u=10ms−1 from the top of a bitlding at time t=0. At time t=5s the particle strikes the fround. Find the height of the building.
 .
.
View SolutionA particle is projected from the ground at an angle such that it just clears the top of a polar after t1 time its path. It takes further t2 time to reach the ground. What is the height of the pole ?
View SolutionA stone is thrown downwards with velocity 10 m/s from the roof of a builng and it reaches the ground with speed 40 m/s. the height of the building would be
View SolutionA particle is projected with initial velocity u=10m/s from a point ( 10m, 0m, 0m ) m along z-axis. At the same time , another particle was also projected with velocity v(ˆi−ˆj+ˆk)m/s from ( 0m, 10m, 0m). It is given that they collide at some point in the space . Then find the value of v. [→g=10m/s2(−ˆk)]
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
 .
.
View SolutionA particle A is projected with an initial velocity of 60m/s at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a)the angle of projection α of particle B, (b) time when the collision takes place and (c) the distance of P from A, where collision occurs. (g=10m/s2)

View SolutionA particle is projected horizontally with a speed u from the top of plane inclined at an angle θ with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA particle is projected vertically up from the top of a tower with velocity 10m/s. It reaches the ground in 5s. Find -
(a) Height of tower
(b) Striking velocity of particle at ground
(c ) Distance traversed by particle.
(d) Average speed & average velocity of particle.
View SolutionA particle moves vertically with an upwards initial speed v0=10.5ms−1. If its acceleration varies with time as shown in a-t graph in figure, find the velocity of the particles at t = 4s.

View SolutionA particle is projected from a tower of height 25 m with velocity 20√2m/s at 45∘. (a) Find the time when particle strikes with ground. (b) The horizontal distance from the foot of tower where it strikes. (c) Also find the velocity at the time of collision.
View Solution
